机器学习中10种损失函数大梳理！建议收藏，你一定用得到

今儿想和大家聊聊关于损失函数方面的问题。

损失函数（Loss Function）是在机器学习和深度学习中用来衡量模型预测值与真实标签之间差异的函数。不同的任务和模型可能需要不同的损失函数。

今天就聊聊下面常见的损失函数，关于原理、使用场景，并且给出完整的代码：

均方误差
平均绝对误差
交叉熵损失
对数损失
多类别交叉熵损失
二分类交叉熵损失
余弦相似度损失
希尔伯特-施密特口袋
Huber损失
感知器损失

ok，咱们一起来学习一下~

1、均方误差

均方误差是一种常用的损失函数，通常用于衡量回归模型预测结果与真实值之间的差异程度。

均方误差是通过计算预测值与真实值之间差异的平方和来衡量模型的性能。它对于较大的差异给予更高的权重，因为平方操作会放大较大的差异。均方误差的数值越小，表示模型预测的结果与真实值越接近。

均方误差的公式：

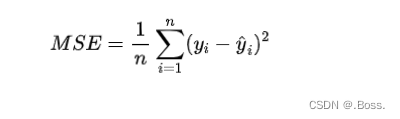
import numpy as np
import matplotlib.pyplot as plt

# 真实值和预测值
y_true = np.array([1, 2, 3, 4, 5])
y_pred = np.array([1.2, 2.5, 3.7, 4.1, 5.3])

# 计算均方误差
mse = np.mean((y_true - y_pred) ** 2)
print("MSE:", mse)

# 绘制真实值和预测值的散点图
plt.scatter(y_true, y_pred)
plt.plot([min(y_true), max(y_true)], [min(y_true), max(y_true)], 'k--', lw=2)  # 绘制直线y=x
plt.xlabel('True Values')
plt.ylabel('Predicted Values')
plt.title('Scatter plot of True vs Predicted Values')
plt.show()

运行这段代码将计算出均方误差，并绘制出一个散点图，其中x轴表示真实值，y轴表示预测值。通过与直线y=x进行比较，可以看到预测值与真实值之间的差异程度。较接近直线的点表示预测结果较准确。

2、平均绝对误差

平均绝对误差（Mean Absolute Error，MAE）是一种用于衡量预测模型性能的损失函数，通常用于回归问题。它衡量了模型的预测值与实际观测值之间的平均绝对差异。MAE 的值越小，表示模型的预测越准确。

MAE 的原理非常简单，它是所有绝对误差的平均值。绝对误差是指每个观测值的预测值与实际值之间的差的绝对值。

平均绝对误差的计算公式：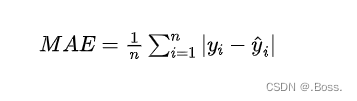

import numpy as np
import matplotlib.pyplot as plt

# 生成随机数据
np.random.seed(0)
n = 50
X = np.linspace(0, 10, n)
y_true = 2 * X + 1 + np.random.normal(0, 1, n)  # 真实的目标值，包含随机噪音
y_pred = 2 * X + 1.5  # 模拟的预测值

# 计算MAE
mae = np.mean(np.abs(y_true - y_pred))

# 绘制数据点和预测线
plt.scatter(X, y_true, label='Actual', color='b')
plt.plot(X, y_pred, label='Predicted', color='r')
plt.title(f'MAE = {mae:.2f}')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

代码中，首先生成了一些随机的数据点，然后计算了 MAE，并用散点图和预测线将数据可视化出来。MAE 的值会显示在图的标题中。

通过这个示例，你可以直观地了解 MAE 的计算和它如何衡量模型的性能。MAE 越小，预测值越接近实际值。

3、交叉熵损失

交叉熵损失（Cross-Entropy Loss）是机器学习中常用的一种损失函数，主要应用于分类问题。它用于衡量模型预测结果与实际标签之间的差异。

交叉熵损失基于信息论中的交叉熵概念，用于度量两个概率分布之间的相似性。在分类问题中，我们将实际标签表示为一个one-hot向量，即只有一个元素为1，其余元素为0；而模型的预测结果通常是一个概率分布。交叉熵损失通过计算实际标签和模型预测结果之间的交叉熵来评估模型的性能。

对于多分类问题，交叉熵损失可以表示为：

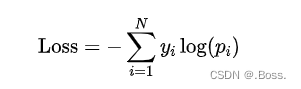
其中，为实际标签中第个类别的概率（one-hot编码），为模型预测的第个类别的概率。

一个Python案例

以下是一个多分类问题的例子，使用交叉熵损失进行模型训练：

import numpy as np
import matplotlib.pyplot as plt

def cross_entropy_loss(y_true, p_pred):
    epsilon = 1e-10  # 添加一个小的常数以避免log(0)计算错误
    return -np.sum(y_true * np.log(p_pred + epsilon), axis=1)

# 模拟数据
num_samples = 1000
num_classes = 5

np.random.seed(42)
y_true = np.eye(num_classes)[np.random.choice(num_classes, num_samples)]  # 生成随机的one-hot标签
p_pred = np.random.rand(num_samples, num_classes)  # 模型预测的概率

loss = cross_entropy_loss(y_true, p_pred)

# 计算平均损失
average_loss = np.mean(loss)

# 绘制损失函数图形
plt.plot(range(num_samples), loss, 'bo', markersize=2)
plt.xlabel('Sample')
plt.ylabel('Cross-Entropy Loss')
plt.title('Cross-Entropy Loss for each Sample')
plt.axhline(average_loss, color='r', linestyle='--', label='Average Loss')
plt.legend()
plt.show()

print(f'Average Loss: {average_loss}')

代码中，首先定义了一个cross_entropy_loss函数来计算交叉熵损失。然后，我们模拟了一个多分类问题的数据集，其中包含1000个样本和5个类别。接下来，使用该函数计算模型预测结果和实际标签之间的交叉熵损失，并计算平均损失。最后，使用Matplotlib库绘制了每个样本的交叉熵损失，并在图形中用一条红色虚线表示平均损失。

在实际应用中，通常会结合优化算法（如梯度下降）来最小化交叉熵损失，并优化模型的预测性能。

4、对数损失

对数损失（Log Loss），也称为二分类交叉熵损失，是机器学习中常用的一种损失函数之一，主要适用于二分类问题。它用于衡量模型预测结果与实际标签之间的差异。

对数损失基于信息论中的交叉熵概念，用于度量两个概率分布之间的相似性。在二分类问题中，通常使用0和1表示实际标签，而模型的预测结果是一个介于0和1之间的概率值。对数损失通过计算实际标签和模型预测结果的交叉熵来评估模型的性能。

对数损失可以表示为：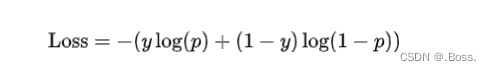

import numpy as np
import matplotlib.pyplot as plt

def log_loss(y_true, p_pred):
    epsilon = 1e-10  # 添加一个小的常数以避免log(0)计算错误
    return - (y_true * np.log(p_pred + epsilon) + (1 - y_true) * np.log(1 - p_pred + epsilon))

# 模拟数据
num_samples = 1000

np.random.seed(42)
y_true = np.random.randint(2, size=num_samples)  # 随机生成0和1的实际标签
p_pred = np.random.rand(num_samples)  # 模型预测的概率

loss = log_loss(y_true, p_pred)

# 计算平均损失
average_loss = np.mean(loss)

# 绘制损失函数图形
plt.plot(range(num_samples), loss, 'bo', markersize=2)
plt.xlabel('Sample')
plt.ylabel('Log Loss')
plt.title('Log Loss for each Sample')
plt.axhline(average_loss, color='r', linestyle='--', label='Average Loss')
plt.legend()
plt.show()

print(f'Average Loss: {average_loss}')

5、多类别交叉熵损失

多类别交叉熵损失是机器学习中常用的一种损失函数，用于衡量模型输出与真实标签之间的差异。它适用于多分类问题，其中每个样本有一个唯一的类别标签。

该损失函数通过计算模型预测的概率分布与真实标签的概率分布之间的交叉熵来度量它们之间的差异。交叉熵是一个非负的值，当且仅当预测的概率分布与真实标签完全匹配时为零。

假设我们有一个样本，其真实标签表示为一个one-hot向量（只有一个元素为1，其他元素为0）。假设模型的输出是一个概率分布向量，表示模型对每个类别的预测概率。则多类别交叉熵损失的公式如下：

其中，是真实标签向量中第个元素的值（0或1），是模型输出的概率分布向量中第个元素的值。

一个Python案例

下面是一个使用Python实现的多类别交叉熵损失的案例。

import numpy as np
import matplotlib.pyplot as plt

def categorical_cross_entropy(y_true, y_pred):
    # 避免出现概率为0的情况，加上一个小的偏移量
    epsilon = 1e-7
    # 计算交叉熵损失
    loss = -np.sum(y_true * np.log(y_pred + epsilon))
    return loss

# 生成随机的真实标签和预测概率分布
np.random.seed(42)
num_classes = 4
num_samples = 1000
y_true = np.random.randint(num_classes, size=num_samples)
y_pred = np.random.rand(num_samples, num_classes)

# 将真实标签转换为one-hot向量
y_true_one_hot = np.eye(num_classes)[y_true]

# 计算多类别交叉熵损失
loss = categorical_cross_entropy(y_true_one_hot, y_pred)
print("Loss:", loss)

# 绘制损失函数的图形
x = np.arange(0.01, 1.0, 0.01)
y = -np.log(x)
plt.plot(x, y)
plt.xlabel("Predicted Probability")
plt.ylabel("Loss")
plt.title("Categorical Cross-Entropy Loss")
plt.show()

在这个案例中，我们首先生成了随机的真实标签和预测概率分布。然后将真实标签转换为one-hot向量，以便与预测概率分布进行计算。

最后，使用categorical_cross_entropy函数计算多类别交叉熵损失，并输出结果。

同时，我们将绘制损失函数图形，其中横轴表示预测的概率，纵轴表示对应的损失值。

6、二分类交叉熵损失

二分类交叉熵损失是机器学习中常用的一种损失函数，适用于二分类问题，其中每个样本只有两个可能的类别。

该损失函数通过计算模型输出的概率与真实标签之间的交叉熵来衡量它们之间的差异。交叉熵是一个非负的值，当且仅当预测的概率与真实标签一致时为零。

假设我们有一个样本，其真实标签表示为0或1。假设模型的输出是一个[0, 1]范围内的概率，表示模型对类别1的预测概率。则二分类交叉熵损失的公式如下：

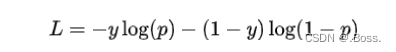
import numpy as np
import matplotlib.pyplot as plt

def binary_cross_entropy(y_true, y_pred):
    # 避免出现概率为0或1的情况，加上一个小的偏移量
    epsilon = 1e-7
    # 计算交叉熵损失
    loss = -y_true * np.log(y_pred + epsilon) - (1 - y_true) * np.log(1 - y_pred + epsilon)
    return loss

# 生成随机的真实标签和预测概率
np.random.seed(42)
num_samples = 1000
y_true = np.random.randint(2, size=num_samples)
y_pred = np.random.rand(num_samples)

# 计算二分类交叉熵损失
loss = binary_cross_entropy(y_true, y_pred)
print("Loss:", loss[:10])  # 打印前10个样本的损失值

# 绘制损失函数的图形
x = np.linspace(0.01, 0.99, 100)
y = -np.log(x) - np.log(1 - x)
plt.plot(x, y)
plt.xlabel("Predicted Probability")
plt.ylabel("Loss")
plt.title("Binary Cross-Entropy Loss")
plt.show()

在这个案例中，我们首先生成了随机的真实标签和预测概率。然后使用binary_cross_entropy函数计算二分类交叉熵损失，并输出结果。同时，我们将绘制损失函数图形，其中横轴表示预测的概率，纵轴表示对应的损失值。

7、余弦相似度损失

余弦相似度损失是一种常用的机器学习损失函数，用于衡量向量之间的相似性。它基于向量的内积和范数来计算相似度，并将其转化为一个损失值。

余弦相似度损失基于余弦相似度的概念。余弦相似度是两个向量之间的夹角的余弦值，范围在-1到1之间。当夹角为0度时，余弦相似度为1，表示两个向量完全相同；当夹角为90度时，余弦相似度为0，表示两个向量无关；当夹角为180度时，余弦相似度为-1，表示两个向量完全相反。

公式表达：假设有两个向量A和B，余弦相似度可以通过以下公式计算：

import numpy as np
import matplotlib.pyplot as plt

# 生成随机数据
np.random.seed(0)
x = np.linspace(-10, 10, 100)
y_true = np.sin(x) + np.random.normal(0, 0.1, size=(100,))

# 定义交叉熵损失函数
def cross_entropy_loss(y_true, y_pred):
    epsilon = 1e-7  # 避免log(0)的情况
    loss = -np.mean(y_true * np.log(y_pred + epsilon) + (1 - y_true) * np.log(1 - y_pred + epsilon))
    return loss

# 假设预测值为正弦函数
y_pred = np.sin(x)

# 计算交叉熵损失
loss = cross_entropy_loss(y_true, y_pred)

# 绘制图形
plt.plot(x, y_true, label='True')
plt.plot(x, y_pred, label='Predicted')
plt.title(f'Cross Entropy Loss: {loss:.4f}')
plt.legend()
plt.show()

上述代码生成了一个包含随机噪声的正弦函数作为真实值，并假设预测值也是正弦函数。通过交叉熵损失函数计算出损失值，并用图形表示出真实值和预测值。注意，这里的交叉熵损失函数假设了二分类问题，因此y_true和y_pred都是取值在0到1之间的概率值。

未完待续。。