什么是查找

在一些数据元素中，通过一定的方法找出与给定关键字相同的数据元素的过程。

什么是列表查找

也叫线性表查找，从列表中查找指定元素

列表查找是一种算法，对应的自然就有输入和输出：

输入：列表、待查找元素
输出：元素下标（未找到元素时一般返回None或-1）

内置列表查找函数：index()

顺序查找（Linear Search）

也叫线性查找，从列表第一个元素开始，顺序进行搜索，直到找到元素或搜索到列表最后一个元素为止。

例如：

def liner_search(li,val):
        """
        li表示列表
        val表示待查找的值
        """
    for ind,v in enumerate(li):
        if v == val:
            return ind
        else:
            return None

enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中。

这个程序的时间复杂度为O(n)，n为列表的长度，顺序查找顾名思义就是将列表循环一遍进行逐个查找。

二分查找（Binary Search）

1、二分查找简介

又叫折半查找，从有序列表的初始候选区li[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。

二分查找适用于有序数组。

三个红色的变量下面会解释到。

2、二分查找的实例

例如：

从列表中查找元素3

待查找的值：3
候选区中间值：mid
候选区：left和right之间

（1）候选区指目标元素存在的区间，那么，如何确定哪一个区间为候选区呢？

我们选择引入两个变量：left 和 right，对应的值为索引序号，如下图，此时left=0，right=8，left和right之间为候选区

（2）候选区中间值引入另外一个变量：mid，mid为left和right的和除以二然后取整

表达式为mid = (left+right) // 2

如图，此时中间值mid = (0+8) // 2=4，注意mid的值表示的意思是列表的索引值

（3）此时，我们知道，候选区在left和mid之间，那么我们可以将right移动到mid的左边（也就是right = mid-1），候选区为left到新的right之间；这样，就缩小了一次候选区。

（4）新的mid如下图，新的mid = (0+3) // 2 = 1，此时候选区为0到3（left到right）

（5）确定新的候选区：此时，mid小于待查找的值3，所以，待查找的值在mid和right之间。上面不是提到了吗，mid>3的时候，需要将right移动到mid的左边（也就是mid-1）；同样的，mid＞3的时候，我们将left移动到mid的右边（left = mid+1），此时新的候选区如下图：

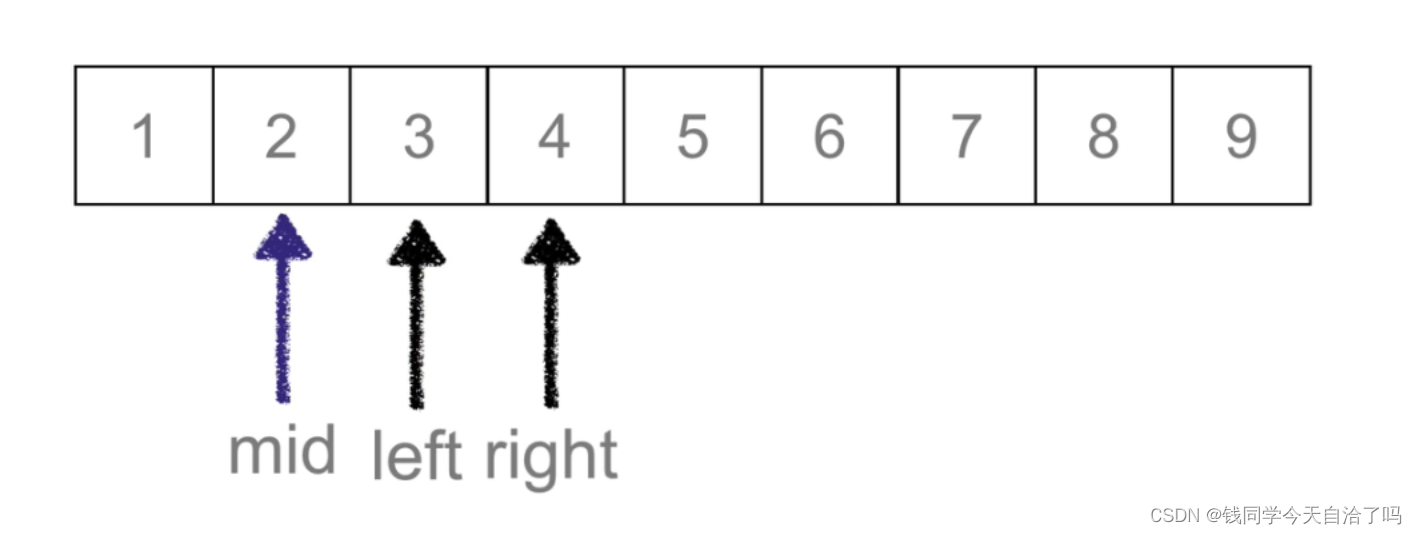
（6）如下图：mid = (2+3) // 2 = 2

mid为2时（mid是索引），对应到列表中的值为3，即是我们要查找的值，输出mid对应的值，程序结束。

（7）如果第（6）点，mid对应值和待查找值不匹配，right = mid - 1 = 1 < left = 2，即right<left，说明在目标列表中没有找到目标元素，那么程序结束，返回None。

3、二分查找实例的代码演示

def binary_search(li,val):
    """
    li是一个列表
    val是目标元素
    """
    left = 0
    right = len(li)-1
    while left <= right: # 候选区有值
        mid = (left+right) // 2
        if li[mid] == val:
            return mid
        elif li[mid] > val: # 待查找的值在mid左侧
            right = mid-1
        else: # li[mid] < val 待查找的值在mid右侧
            left = mid+1
    else:
        return None

代码完成后，可以尝试用DEBUG模式进行调试，会发现和预期结果一致，证明程序无误。