文章目录
- 一、线性回归模型建模准备
- 1. 数据准备
- 2. 模型准备
- 二、线性回归模型训练
- 1. 模型训练的本质:有方向的参数调整
- 1.1 模型训练与模型参数调整
- 1.2 模型评估指标与损失函数
- 1.3 损失函数与参数求解
- 2. 利用最优化方法求解损失函数
- 2.1 损失函数的求解
- 2.2 图形展示损失函数
- 2.3 函数的凹凸性
- 2.4 最小二乘法理论基础
- 2.5 最小二乘法求解 SSELoss
一、线性回归模型建模准备
- 在了解完基本的概念和流程之后,我们尝试手动实现线性回归模型。
1. 数据准备
- 线性回归是属于回归类模型,是针对连续性变量进行数值预测的模型,因此需要选用 abalone 数据集进行建模。
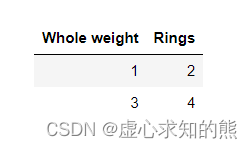
- 此处为了更加清晰的展示建模过程的内部计算细节,我们选取数据集中部分数据带入进行建模。
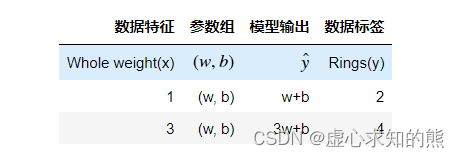
2. 模型准备
- 不难看出,上述数据集是极端简化后的数据集,只有一个连续型特征和连续型标签,并且只包含两条数据。围绕只包含一个特征的数据所构建的线性回归模型,也被称为简单线性回归。
- 简单线性回归的模型表达式为 y=wx+b,其中:
- x 表示自变量,即数据集特征;
- w 表示自变量系数,代表每次计算都需要相乘的某个数值;
- b 表示截距项,代表每次计算都需要相加的某个数值;
- y 表示因变量,即模型输出结果。
- 除了简单线性回归外,线性回归主要还包括多元线性回归和多项式回归两类。
- 其中,多元线性回归用于解决包含多个特征的回归类问题,模型基本表达式为:y=w1x1+w2x2+…+wnxn+b,其中:
- x1…n 表示 n 个自变量,对应数据集的 n 个特征;
- w1…n 表示 n 个自变量的系数;
- b 表示截距。
- 此外,多项式回归则是在多元线性回归基础上,允许自变量最高次项超过1次。
- 准备好了数据和算法之后,接下来就是模型训练过程。
二、线性回归模型训练
1. 模型训练的本质:有方向的参数调整
1.1 模型训练与模型参数调整
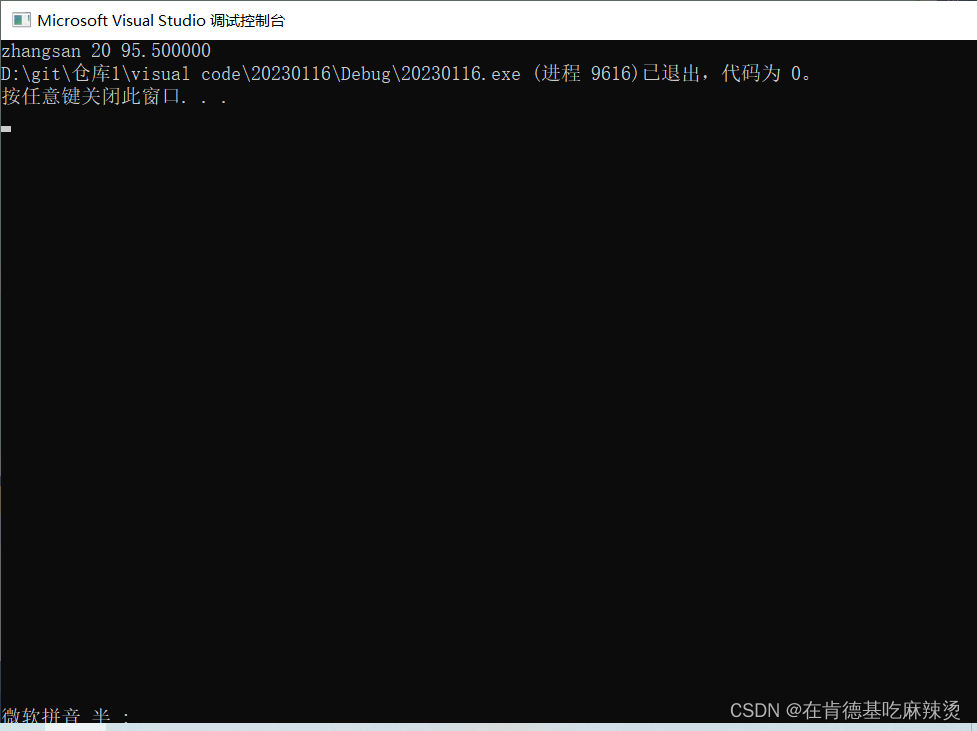
- 模型训练就是指对模型参数进行有效调整。
- 模型参数是影响模型输出的关键变量,例如本例中的模型包含两个参数, w1 和 b ,当参数取得不同值时,模型将输出完全不同的结果。
- 其中简单线性回归计算过程为 y=wx+b。
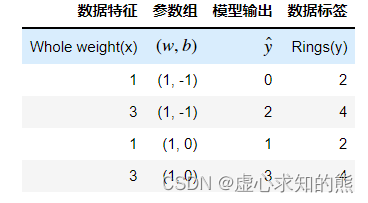
- 需要说明的是,在很多场景下,我们会使用更加简洁的记号用于代表模型训练过程中的各项数值,譬如:
- xi 表示某条数据第 i 个特征的取值;
- y 作为某条数据的标签取值;
- ŷ 表示某条数据带入模型之后模型输出结果。
- 从上式不难看出,模型参数取值不同模型输出结果也不同,而不同组的参数取值似乎也有好坏之分。
- 当参数组取值为 (1,0)时的模型输出结果,要比参数组取值为(1,-1)时输出结果更加贴近真实值。
- 这其实也就说明第二组参数要好于第一组参数。而机器在学习的过程,或者说模型训练过程,就是需要找到一组最优参数。
1.2 模型评估指标与损失函数
- 既然有了模型输出结果好与坏的判别,我们就需要将这种反馈有效的传递给模型,才能够让模型在训练过程中逐渐朝向好的方向发展。而要在模型训练过程中建立这种有效的反馈,我们就必须先掌握两个基本概念,即模型评估指标与损失函数。
- 其中,模型评估指标是指评估模型输出结果好与坏的标量计算结果,其最终结果一般由模型预测值 ŷ 和真实值 y 共同计算得出。
- 而对于回归类问题,最重要的模型评估指标就是 SSE ——残差平方和。
- 残差平方和,指的是模型预测值 ŷ 和真实值 y 之间的差值的平方和,计算结果表示预测值和真实值之间的差距,结果越小表示二者差距越小,模型效果越好。SSE基本计算公式如下。
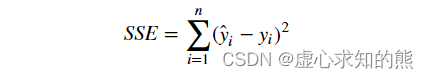
- 其中 n 为样本数量。对应的,上述两组不同参数取值对应的模型残差平方和计算结果依次如下。
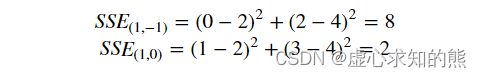
- 能够看出,第二组参数对应模型效果更好。据此我们就找到了能够量化评估模型效果好坏的指标。
- 和模型评估指标是真实值和预测值的计算过程不同,模型的损失函数都是关于模型参数的函数。
- 损失函数本质上一个衡量模型预测结果和真是结果之间的差异的计算过程,例如在 SSE 中如果带入模型参数,则就能构成一个 SSE 损失函数,基本计算过程如下如下。
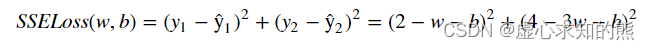
- SSELoss 的基本计算过程和 SSE 一致,只不过 SSELoss 中带入的是模型参数,而 SSE 带入的是确定参数值之后的计算结果。
- 因此我们也可以认为对于 SSELoss 和 SSE 来说,一个是带参数的方程,一个是确定方程参数之后的计算结果。
- 既然 SSE 和 SSELoss 的计算过程类似,那为何要区别损失函数和模型评估指标呢?主要有以下两点原因。
- (1) 对于很多模型(尤其是分类模型)来说,模型评估指标和模型损失函数的计算过程并不一致,例如准确率就很难转化为一个以参数为变量的函数表达式。
- (2) 模型评估指标和损失函数构建的目标不同,模型评估指标的计算目标是给模型性能一个标量计算结果,而损失函数的构建则是为了找到一组最优的参数结果。
- 除了 SSE 以外,常用的回归类问题的评估指标还有 MSE(均方误差)和 RMSE(均方根误差),其中 MSE 就是在 SSE 的基础上除以样本总量。
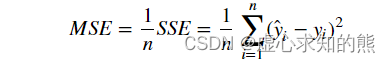
- 而 RMSE 则是在 MSE 基础之上开平方算得的结果。
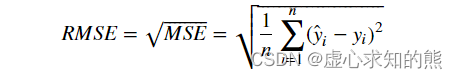
- 对应的,MSE 和 RMSE 也有相对的损失函数。
1.3 损失函数与参数求解
- 一旦损失函数构建完成,我们就可以围绕损失函数去寻找损失函数的最小值,以及求出损失函数取得最小值时函数自变量(也就是模型参数)的取值,此时参数的取值就是原模型中参数的最优取值结果。
- 这点从 SSE 和 SSELoss 彼此类似的计算过程能够很容易看出来,由于我们最终建模目标是希望模型预测结果和真实结果一致,也就是 SSE 的取值尽可能小,而 SSE 的值是 SSELoss 中的两个变量(w,b)取值决定的。
- 因此如果我们能找到一组(w,b)使得 SSE 的最终计算结果尽可能的小,也就相当于找到了一组模型的最佳参数。
- 由此可得,损失函数的核心作用主要是搭建参数求解的桥梁,构建一个协助模型求解参数的方程。
- 通过损失函数的构建,我们可以将求解模型最优参数的问题转化为求解损失函数最小值的问题。至此也就完成了此前所说的确定反馈传递反馈的过程。
- 值得注意的是,损失函数的计算方程和实际带入进行建模的数据直接相关,上述 SSELoss 是在带入两条数据的情况下构建的损失函数,而调整输入数据,损失函数实际计算方程也会发生变化。
2. 利用最优化方法求解损失函数
2.1 损失函数的求解
- 在构建好损失函数之后,接下来就是如何求解损失函数的最小值(及损失函数取得最小值时 w 和 b 的取值)。
- 值得注意的是,此时损失函数是一个关于模型参数的方程,也就是说模型参数此时成了损失函数的自变量。
- 要求解损失函数最小值,就需要记住一些优化理论和优化算法。当然,此处的优化理论和算法都是一些无约束条件下进行函数极值求解的方法。利用优化方法求解损失函数最小值及其取得最小值时损失函数自变量(也就是模型参数)的取值过程,也被简称为损失函数求解。
2.2 图形展示损失函数
- 为了更好的讨论损失函数(SSELoss)求最小值的过程,对于上述二元损失函数来说,我们可以将其展示在三维空间内:三维空间坐标分别为 w、b、SSELoss。此处我们可以使用 Python 中 matplotlib 包和 Axes3D 函数进行三维图像绘制。
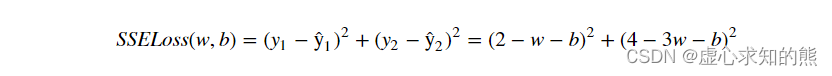
- 在 Jupyter Notebook 中输入如下代码(** 表示幂运算)。
# 导入相关包
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x = np.arange(-1,3,0.05)
y = np.arange(-1,3,0.05)
w, b = np.meshgrid(x, y)
SSE = (2 - w - b) ** 2 + (4 - 3 * w - b) ** 2
ax = plt.axes(projection='3d')
ax.plot_surface(w, b, SSE, cmap='rainbow')
#生成z方向投影,投到x-y平面
ax.contour(w, b, SSE, zdir='z', offset=0, cmap="rainbow")
#x轴标题
plt.xlabel('w')
#y轴标题
plt.ylabel('b')
plt.show()
- 会得到如下的实现图像。
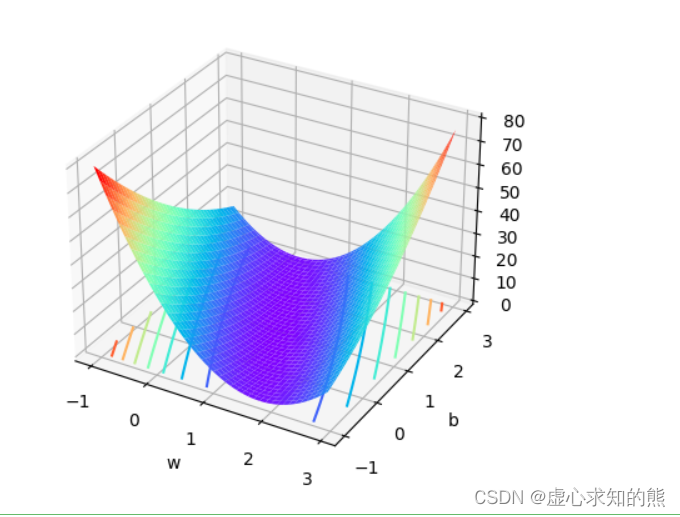
- 根据图像,我们大概能判断损失函数最小值点位置。
2.3 函数的凹凸性
- 初步探索函数图像,不难看出,目标函数是个整体看起来向下凸的函数。
- 从理论出发我们知道,函数的凹凸性是函数的重要性质,也是涉及到损失函数求解方法选取的重要性质。这里我们首先给出凸函数的一般定义,对于任意一个函数,如果函数 f(x) 上存在任意两个点,x1,x2 ,且满足如下性质,就判定为凸函数。
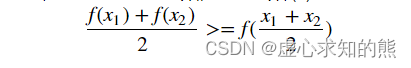
- 很多机器学习模型所构建的损失函数都是凸函数,因此关于凸函数的优化方法(找到最小值的方法)也就成了机器学习建模过程中最常用的优化方法。
- 而对于一个凸函数来说,全域最小值明显存在。求解凸函数的最小值有很多种方法,其中最为基础的方法叫做最小二乘法。但对于上述 SSELoss,本质上也是一个凸函数。
- 因此我们是可以通过最小二乘法对 SSELoss 进行求解的。
2.4 最小二乘法理论基础
- 我们先抛开公式、从一个简单的角度理解最小二乘法。
- 通过函数的凹凸性可得,在最小值点左边函数逐渐递减、而在最小值点右边函数逐渐递增,最小值点左右两边函数单调性相反。
- 而这种性质其实可以拓展为凸函数的一个关于求解最小值的一般性质,即:
- (1) 对于一元函数,如果存在导数为 0 的点,则该点就是最小值点。
- (2) 对于多元函数,如果存在某一点,使得函数的各个自变量的偏导数都为 0,则该点就是最小值点。
- 据此,我们就找到了最小二乘法求解凸函数最小值的基本出发点:即通过寻找损失函数导函数(或者偏导函数联立的方程组)为 0 的点,来求解损失函数的最小值。
2.5 最小二乘法求解 SSELoss
- 接下来,尝试利用最小二乘法求解 SSELoss。根据上述理论,我们使用最小二乘法求解 SSELoss ,即
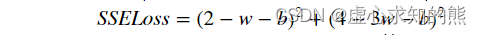
- 本质上就是在找到能够令损失函数偏导数取值都为零的一组 (w,b) 。SSELoss 的两个偏导数计算过程如下:
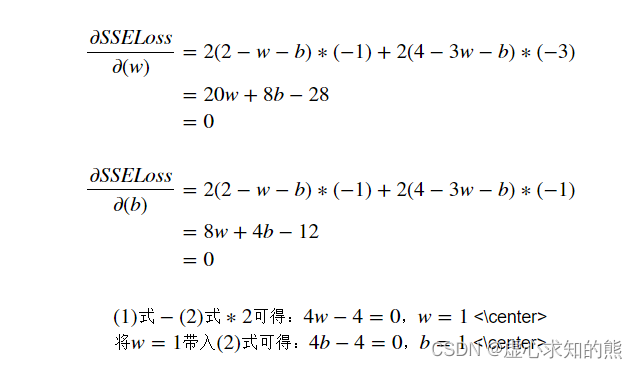
- 最终可得,损失函数最小值点为 (1,1),即当 w=1,b=1 时模型损失函数计算结果最小、模型 SSE 取值最小、模型效果最好,此时 SSE=0,线性回归模型计算结果为:y=x+1。
- 至此,我们就基本完成了一个简单线性回归的模型建立。