前缀和

题目描述

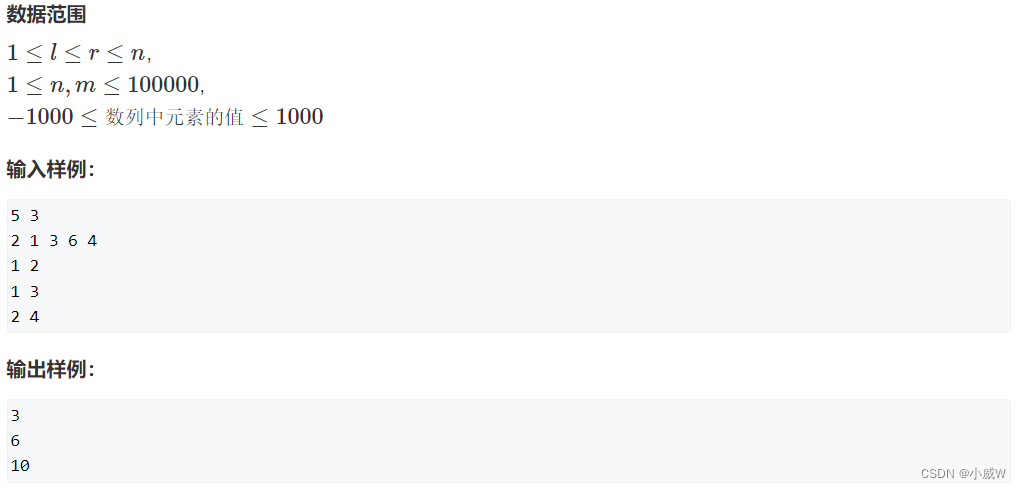
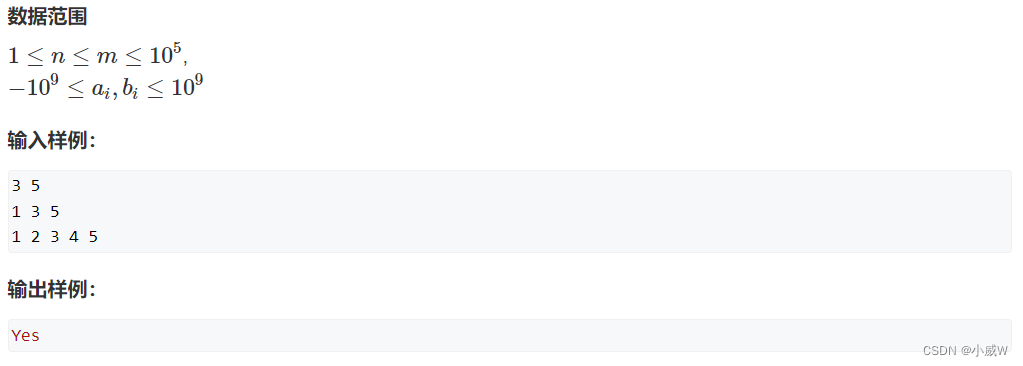
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问，每个询问输入一对 l,r。
对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。

解法

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int main()
{
    int n, m, l, r;
    scanf("%d%d", &n, &m);
    int a[n], s[n + 1];     // s设置为n+1是为了后面计算方便
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    
    s[0] = 0;
    for (int i = 0; i < n; i ++ ) s[i + 1] = s[i] + a[i];
    
    while (m -- ) {
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l - 1]);	// 这里的l和r是1~n范围
    }
    return 0;
}

讲解

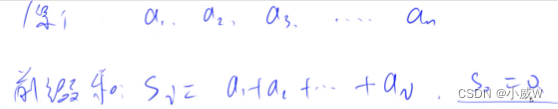
有 a1,a2,a3,a4,a5…
想求a2+a3+a4，则只需s4-s1 = (a1+a2+a3+a4) - (a1) = a2+a3+a4。

---

这道题中可以不初始化 s[0] = 0，事实上，他是任何数都可以，（因为它总是会被消去）。

二维前缀和

题目描述

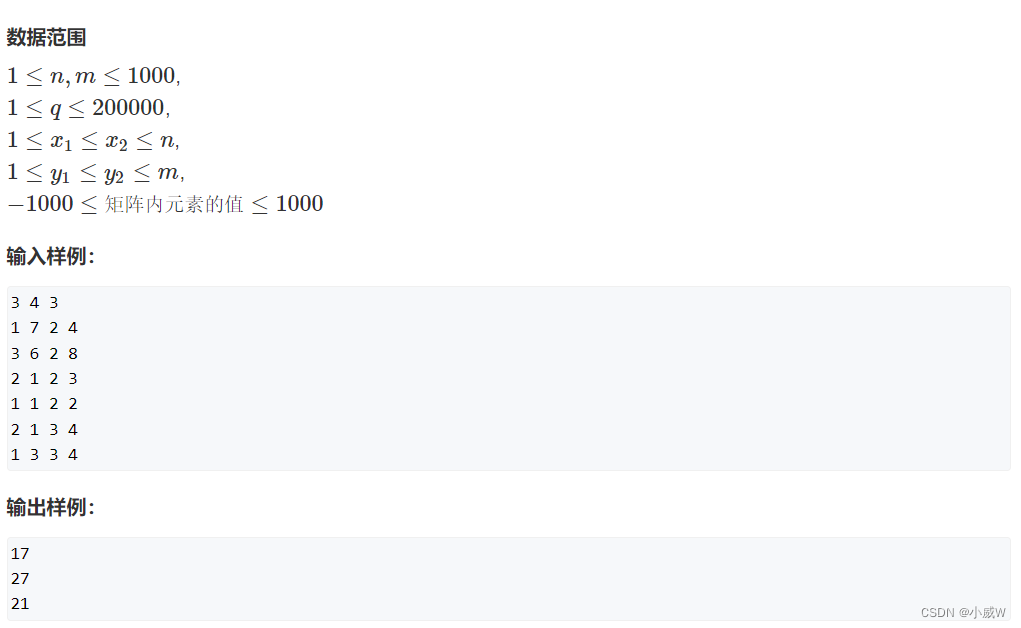
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

解法

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int main()
{
    int n, m, q, x1, y1, x2, y2;
    scanf("%d%d%d", &n, &m, &q);
    int a[n][m], s[n + 1][m + 1];
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            scanf("%d", &a[i][j]);
            s[i + 1][j + 1] = a[i][j] + s[i + 1][j] + s[i][j + 1] - s[i][j];
        }
    }
    
    while (q--) {
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }
    
    return 0;
}

讲解

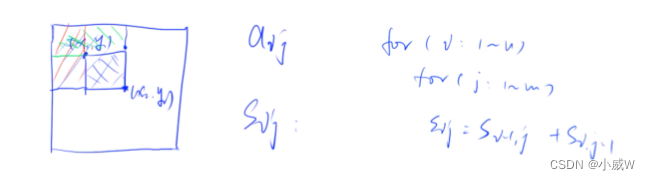
主要看这张图，类似于求面积。

求s：
s[i + 1][j + 1] = a[i][j] + s[i + 1][j] + s[i][j + 1] - s[i][j];

(x1,y1),(x2,y2)之间的和：
s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]

差分

题目描述

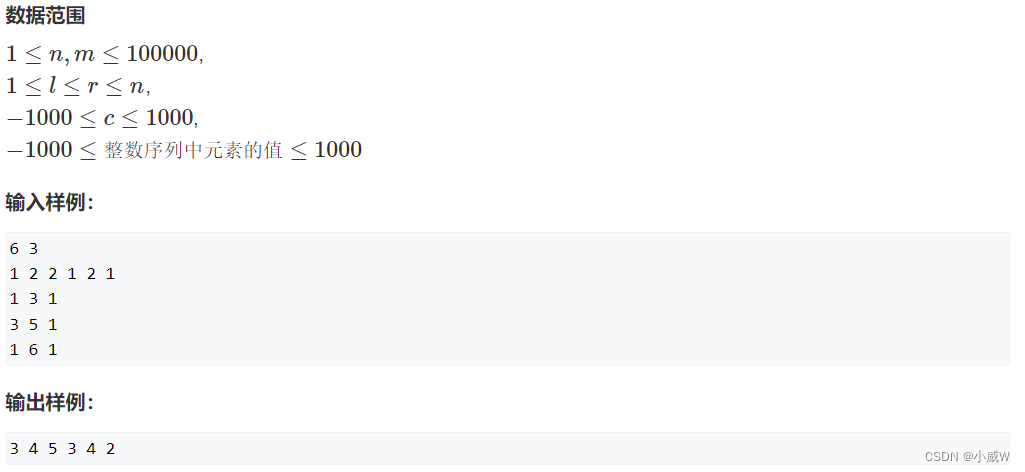
输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

解法

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int main()
{
    int n, m, l, r, c;
    scanf("%d%d", &n, &m);
    int a[n + 1], b[n + 1]; // b是a的差分
    a[0] = 0;
    memset(b, 0, sizeof b);
    for (int i = 1; i <= n; i ++ ) {
        scanf("%d", &a[i]);
        b[i] = a[i] - a[i - 1];
    }
    
    while (m -- ) {
        scanf("%d%d%d", &l, &r, &c);
        b[l] += c;
        b[r + 1] -= c;
    }
    
    for (int i = 0; i < n; ++i) {
        a[i + 1] = a[i] + b[i + 1];
        printf("%d ", a[i + 1]);
    }
    
    return 0;
}

讲解

b 数组是 a 数组的差分，a 数组是 b 数组的前缀和。
那么，a中某一段变量同时变了一个数，相当于b中对应的两个数（开头和结尾）的变化。

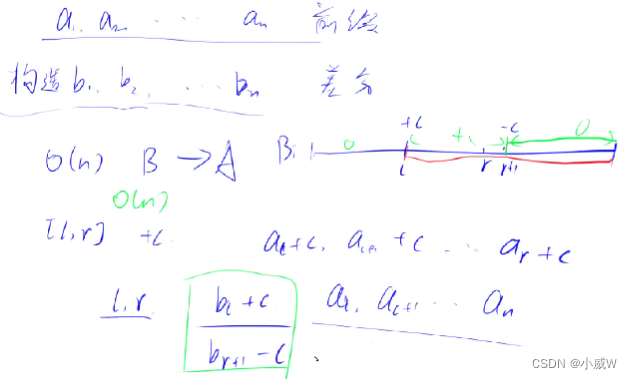
二维差分

题目描述

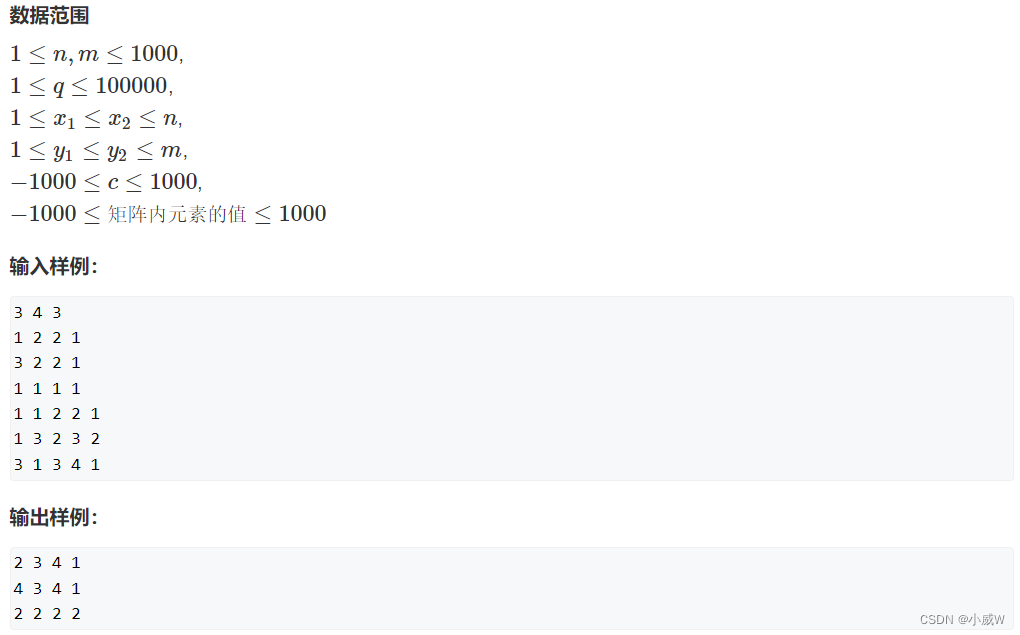
输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

解法

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1005;
int a[N][N], b[N][N];	// 开大一点可以减少越界的麻烦

int main()
{
    int n, m, q, x1, y1, x2, y2, c;
    scanf("%d%d%d", &n, &m, &q);
    
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            scanf("%d", &a[i][j]);
            b[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];
        }
    }
    
    while (q -- ) {
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
        b[x1][y1] += c;
        b[x2 + 1][y2 + 1] += c;
        b[x1][y2 + 1] -= c;
        b[x2 + 1][y1] -= c;
    }
    
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            a[i][j] = b[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
            printf("%d ", a[i][j]);
        }
        printf("\n");
    }
    
    return 0;
}

讲解

这里同样可以在脑海中想象那个正方形来帮助写代码。