说明
【数据结构与算法之美】专栏学习笔记
什么是数组?
数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型的数据。
线性表和非线性表
线性表(Linear List):就是数据排成像一条线一样的结构,每个线性表上的数据最多只有前和后两个方向,比如:数组,链表、队列、栈都是线性表结构。非线性表:数据之间并不是简单的前后关系,比如二叉树、堆、图等。
数组是如何实现根据下标随机访问数组元素的?
随机访问的意思,就是可以随机选择下标,进行数据访问,根据下标随机访问的时间复杂度为 O(1)。
如下图:计算机给数组 int a[10],分配了一块连续内存空间 1000~1039。
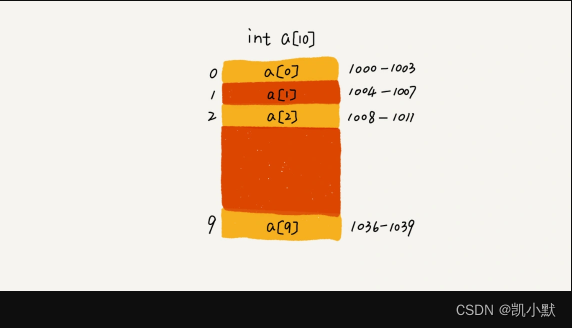
当计算机需要随机访问数组中的某个元素时,会首先通过计算机寻址公式计算出该元素存储的内存地址:
a[i]_address = base_address + i * data_type_size
data_type_size:表示数组中每个元素的大小,a[10] 是 int 类型,该值为 4 个字节base_address:内存块的首地址,a[10] 这里就是 1000
插入和删除操作为什么低效?
插入操作
假设数组的长度为 n,如果将一个数据插入到数组中的第 k 个位置,那么需要将第 k~n 这部分的元素都顺序地往后挪一位,把第 k 个位置腾出来给新来的数据。
插入操作的时间复杂度分析:
- 最坏时间复杂度为:开头插入元素,所有的数据都需要依次往后移动一位,时间复杂度为 O(n)
- 最好时间复杂度:末尾插入元素,无需移动,时间复杂度为 O(1)
- 平均时间复杂度:插入到每一个位置的概率都是
1/n,插入到数组的第一个位置需要移动 n 个元素;插入到数组的第二个位置需要移动 n -1 个元素,以此类推,插入到数组中的最后一个位置,需要移动1个元素.,(n + n - 1 + n - 2 + ... + 1)/n = (n+1)/2,时间复杂度为 O(n)
如果数组中存储的数据并没有任何规律,数组只是被当作一个存储数据的集合,直接将第 k 位的数据搬移到数组元素的最后,把新的元素直接放入第 k 个位置,这样时间复杂度就会降为 O(1)。
示意图如下:

删除操作
如果要删除第 k 个位置的数据,为了内存的连续性,需要移动数据。
删除操作的时间复杂度分析:
- 最坏时间复杂度为:删除开头的数据,所有的数据都需要依次往前移动一位,时间复杂度为 O(n)
- 最好时间复杂度:删除数组末尾的数据,无需移动,时间复杂度为 O(1)
- 平均时间复杂度:和插入类似,时间复杂度为 O(n)
如果不一定非得追求数组中数据的连续性,可以将多次删除操作集中在一起执行,提高删除的效率。比如:标记清除垃圾回收算法里就有用到。
数组访问越界问题
看个例子:
int main(int argc, char* argv[]){
int i = 0;
int arr[3] = {0};
for(; i <= 3; i++){
arr[i] = 0;
printf("hello world\n");
}
return 0;
}
如果 i < 3,那么结果输出如下:

上面这段代码是 i <= 3,当 i = 3 时,数组 a[3] 访问越界,而 a[3] 内存地址指向的是 i 对应内存地址的位置,所以修改 a[3] 的值,也就是修改 i 的值,这时 i 也等于 0,就出现了死循环。

因为 C 语言里并没有规定数组访问越界时编译器应该如何处理,而 Java 会做越界检查,超出就会抛出:java.lang.ArrayIndexOutOfBoundsException。,访问数组的本质就是访问一段连续内存,只要数组通过偏移计算得到的内存地址是可用的,那么程序就可能不会报任何错误。
数组从 0 开始编号的原因
- 底层计算机寻址指令可以少计算一个减法
- 历史原因:沿用了 C 语言从 0 开始计数的习惯
从数组存储的内存模型上来看,下标最确切的定义应该是偏移(offset)。
a[0] 表示偏移为 0 的位置,也就是首地址,a[k] 表示偏移 k 个 type_size 的位置,计算 a[k] 的内存地址:
a[k]_address = base_address + k * type_size
如果从 1 开始计算,每次随机访问数组元素都多了一次减法运算,对于 CPU 来说,就是多了一次减法指令。
a[k]_address = base_address + (k - 1) * type_size
JavaScript 中的数组
JavaScript 中的数组数据可以是不同类型,它的语法相对宽松。
数组的创建与读写
字面量方式创建数组:
var kaimo = [3, 1, 3];
构造函数方式创建数组:
var kaimo = new Array(3, 1, 3);
判断一个对象是否是数组:
Array.isArray(kaimo);
可以使用循环读写数组:
var kaimo = [3, 1, 3];
for (var i = 0; i < kaimo.length; i++) {
console.log(kaimo[i]);
}
数组的深复制与浅复制
- 浅复制:当把数组赋给另外一个数组,然后改变其中一个数组的值,另一数组也会随之改变,这就是数组的浅复制。
- 深复制:指的就是不改变原来的数组而去创建一个新的数组,这种情况是经常使用的,为了不破坏原数组。
存取函数
JavaScript 提供了一组用来访问数组元素的函数,叫存取函数。最常用的存取函数就是 indexOf() 函数,还有 join 和 toString 函数,concat 和 splice 函数。
可变函数
不去引用数组中的某个元素,就能改变数组内容,这种函数称它为可变函数。
push()方法可以在数组末尾添加元素unshift()方法可以在数组开头添加元素pop()可以删除数组末尾的元素shift()删除数组的第一个元素splice()不仅可以用来删除元素,还可以添加元素进数组sort()可以为数组排序reverse()将数组内的元素翻转
sort() 方法用原地算法对数组的元素进行排序,并返回数组。默认排序顺序是在将元素转换为字符串,然后比较它们的 UTF-16 代码单元值序列时构建的。
var kaimo = [30, 100, 40, 500, 200];
kaimo.sort();
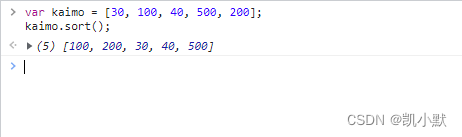
解决这种排序的错误:在调用 sort() 的时候传入一个函数,该函数可以比较出大小。
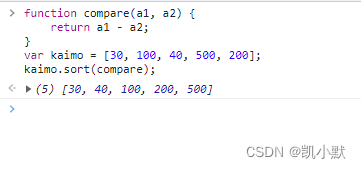
function compare(a1, a2) {
return a1 - a2;
}
var kaimo = [30, 100, 40, 500, 200];
kaimo.sort(compare);
迭代器方法
迭代函数通过对数组中的元素逐个应用,来操作返回相应的值。
不返回新数组: forEach() 、every()、some()、reduce()
every()返回值为布尔类型,对于应用的所有元素,该函数返回 true,则该方法返回 truesome()与every()的不同就是只要有一个元素使改函数返回 true ,那么该方法就返回 truereduce()可以对数组元素进行求和、也能将数组元素连接成字符串。
返回新数组: map() 、filter()
map 的作用与 forEach 是一样的,区别就是 map 函数返回的是一个新数组。
filter 和 every 相似,区别在于当所有的元素使改函数为 true 时,它并不返回布尔类型,而是返回一个新数组。
二维数组
JavaScript 可以通过在数组里在嵌套一个数组来形成二维数组。
var kaimo = [
[11, 12, 13, 14],
[21, 22, 23, 24],
[31, 32, 33, 34],
[41, 42, 43, 44]
];
console.log(kaimo[1][2]); // 23
二维数组的处理可以分为两种:
- 按列访问,外层循环对应行,内层循环对应列。
- 按行访问,外层循环对应列,内层循环对应行。
JavaScript 可以处理一些参差不齐的数组,JavaScript 可以处理运行而不报错。
对象数组
数组里面的元素可以是对象,可以用 push() 等操作方法来操作对象数组。