Day 41 343.整数拆分 96.不同的二叉搜索树

news2024/12/23 1:51:37

整数拆分

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。返回你可以获得的最大乘积。

示例 1:

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。

题解思路大致如下：

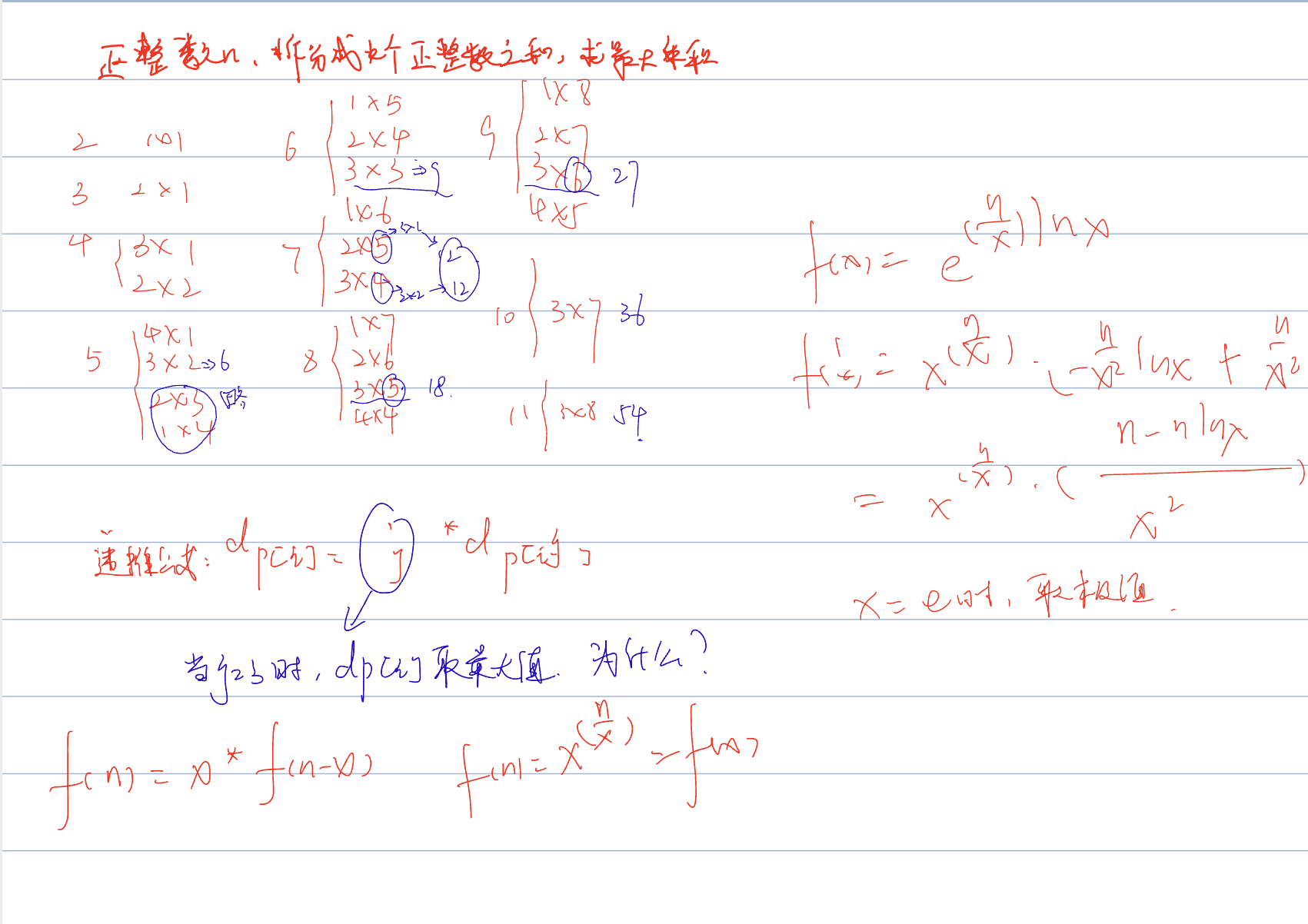
95BEC9AEC9CB8A1399C49FB3BBE4365C

更加严格的证明如下（原题为1976年imo第四题）：
1976IMO

那么思路就明了了，对于n > 4的情况，尽可能的将数分解为3的和，递推公式即为dp[i] = dp[i - 3] *3;

动态规划五部曲：

1.确定dp数组及其下标含义：

此处定义一维数组dp[i]，下标i对应的是正整数的值，dp[i]则对应的是最大的正整数乘积；

2.确定递推公式：

dp[i] = dp[i - 3]*3(i > 4)

3.dp数组如何初始化：
dp[0] = 1, dp[1] = 1, dp[2] = 2, dp[3] = 4;即对应i <= 4的情况下的值，这样可以统一返回dp[i]，不用做多次处理；

4.dp数组应该如何遍历：

本题很显然是从左到右顺序遍历；

5.打印dp数组：

1 1 2 4 6 9 12 18 27 36 54 81 108 162 ……

代码实现如下：

#include<iostream>
#include<stdio.h>
#include<vector>
using namespace std;

class Solution {
private:
	int integerBreak(int n) {
		vector<int> dp(n+1);

		//dp[0] = 1;//不用初始化，因为n >= 2
		if (n == 2)	return 1;
		else if (n == 3)	return 2;
		else if (n == 4)	return 4;
		else if (n == 5)	return 6;
		dp[1] = 1;
		dp[2] = 2;
		dp[3] = 4;
		dp[4] = 6;
		dp[5] = 9;
		for (int i = 6; i <= n; i++) {
			dp[i] = dp[i - 3] * 3;
		}
		return dp[n - 1];
	}
public:
	int test(int n) {
		return integerBreak(n);
	}
};
int main() {
	cout << "Please enter the target integer:(n >= 2)" << endl;
	int n;
	cin >> n;
	Solution mySolution;
	int res = mySolution.test(n);
	cout << "The Max product is:" << res << endl;
	cout << "the dp array will be shown as below:" << endl;
	for (int i = 2; i <= n; i++) {
		cout << mySolution.test(i) << " ";
	}
	cout << endl;
	return 0;
}

很明显，这段代码是有很大的缺陷的，首先是初始化的过程太繁琐，理应有更简单的方法，其次由于初始化的时候已经初始化到了dp[5]，所以一开始就需要n >= 4的时候才能正常运行，不然会报数组越界的错，最后就是这道题与其说是动态规划，更不如说是像贪心；

重新考虑第二步递推公式：

拆分整数有两种方法，即拆分成两数相乘和多数相乘：

一个是j * (i - j) 直接相乘；

一个是j * dp[i - j]，相当于是拆分(i - j)；

考虑简化：

	int integerBreak(int n) {
		vector<int> dp(n+1);
		dp[2] = 1;
		for (int i = 3; i <= n; i++) {
			for (int j = 1; j < i - 1; j++) {
				dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
			}
		}
		return dp[n];
	}

不同的二叉搜索树

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

示例:

先举例看看n = 1和n = 2时：

n = 3:

当①为头节点时，其右子树的布局和n= 2的情况类似；

当②为头节点时，其子树布局和n = 1时类似；

当③为头节点时，其左子树布局也和n = 2时一致；

①为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量

②为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量

③为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]；

所以递推公式可以得到dp[i] += dp[j -1]*dp[i - j];

递推五部曲：

1.确定dp数组以及下标的含义：

dp[i] :节点1到节点i组成的二叉搜索树的个数为dp[i]；

2.确定递推公式：

dp[i] += dp[j -1]*dp[i - j];

j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量

3.dp数组初始化：

从定义上来讲，空节点也是一棵二叉树，也是一棵二叉搜索树;

从递归公式上来讲，dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0，也需要dp[以j为头结点左子树节点数量] = 1，否则乘法的结果就都为0；

即dp[0] = 1;

4.确定遍历顺序：

由递归公式：dp[i] += dp[j -1]*dp[i - j];

节点数为i的状态是依靠 i之前节点数的状态;

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= i; j++) {
        dp[i] += dp[j - 1] * dp[i - j];
    }
}

5.举例dp数组：

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1);
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
};