⚠申明： 未经许可，禁止以任何形式转载，若要引用，请标注链接地址。 全文共计3077字，阅读大概需要3分钟
🌈更多学习内容， 欢迎👏关注👀【文末】我的个人微信公众号：不懂开发的程序猿
个人网站：https://jerry-jy.co/

❗❗❗知识付费，🈲止白嫖，有需要请后台私信或【文末】个人微信公众号联系我

衡量声音之间的距离-理解DTW

---

一、任务需求

Dynamic Time Warping（简称：DTW）算法诞生有一定的历史了（日本学者Itakura提出），它出现的目的也比较单纯，是一种衡量两个长度不同的时间序列的相似度的方法。应用也比较广，主要是在模板匹配中，比如说用在孤立词语音识别（识别两段语音是否表示同一个单词），手势识别，视频动作识别，数据挖掘和信息检索等中，曾经是语音识别的一种主流方法。

我们知道，声音是一组时序数据，正如点雨点之间存在距离一样，时序数据和时序数据之间同样存在距离，显然，不同的衡量标准，会带来不同的距离。

那么声音和声音之间的距离该如何度量呢？想象一下，我们发音"a"，和发音"b"的距离，显然要大于和拉长声音说了一个"a~"的距离。

事实上，在声音距离里，我们希望发音"a"，和发长音"a~"的距离为0，因为我们知道这是两个同样的音。

为了衡量声音（或其他一切可以定义距离的数据），人们发明了DTW的距离度量方法。DTW示意如下：

显然，对于声音来说，我们认为蓝红两个声音并没有什么不同，不过是有些音阶被拉长或缩短了一些，而DTW在计算距离的时候，会充分考虑发音的伸缩问题。

要求：学习使用DTW/动态时间扭曲方法度量多种数据之间的距离。

二、任务目标

1、学习使用DTW计算一维数组之间的距离

2、学习使用DTW计算二维数组之间的距离

3、学习使用DTW计算一维字符串之间的距离

4、学习使用DTW计算声音之间的距离

三、任务环境

1、jupyter开发环境

2、python3.6

3、tensorflow2.4

四、任务实施过程

加载工具包

import sys

sys.path.append('/home/jovyan/dependences/')

import numpy as np
from matplotlib import pyplot as plt
from dtw import dtw

自定义距离度量可视化工具函数

def plt_distance(dist, cost, acc, path):
    plt.imshow(cost.T, origin='lower', cmap=plt.cm.Reds, interpolation='nearest')
    plt.plot(path[0], path[1], '-o')
    plt.xticks(range(len(x)), x)
    plt.yticks(range(len(y)), y)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.axis('tight')
    plt.title('Minimum distance: {}'.format(dist))
    plt.show()

1、一维数组之间的距离

首先我们尝试观察两组完全一样的数组，DTW度量的距离。显然我们期望距离是0

from sklearn.metrics.pairwise import manhattan_distances
x = [0, 0, 1, 1, 2, 4, 2, 1, 2, 0]
y = [0, 0, 1, 1, 2, 4, 2, 1, 2, 0]
dist_fun = manhattan_distances

这是两个一维数组，因此我们可以使用曼哈顿距离进行度量，接下来计算数组之间的距离。

dist, cost, acc, path = dtw(x, y, dist_fun)
plt_distance(dist, cost, acc, path)

可以看到，数组中逐元素的距离都是0，整体数组之间的距离也是0，这和我们的预期一致。

接下来我们将尝试“拉长”数组y（想象一下，拉长发音"a"的样子）。

x = [0, 0, 1, 1, 2, 4, 2, 1, 2, 0]
y = [0, 0, 1, 1, 1, 2, 2, 4, 2, 1, 2, 0, 0]

在这里我们随机“拉长”了一些元素，来模拟拉长发音这个操作，注意，各元素的相对位置和数值并没有发生变化，只有数量发生了变化。

dist, cost, acc, path = dtw(x, y, dist_fun)
plt_distance(dist, cost, acc, path)

可以看到，尽管两个数组并不是完全相同，但其距离依然是0，这和我们预期一致。

接下来我们将使用两个完全不同的数组。

x = [0, 0, 1, 1, 2, 4, 2, 1, 2, 0]
y = [1, 1, 1, 2, 2, 2, 2, 3, 2, 0]

dist, cost, acc, path = dtw(x, y, dist_fun)

plt_distance(dist, cost, acc, path)

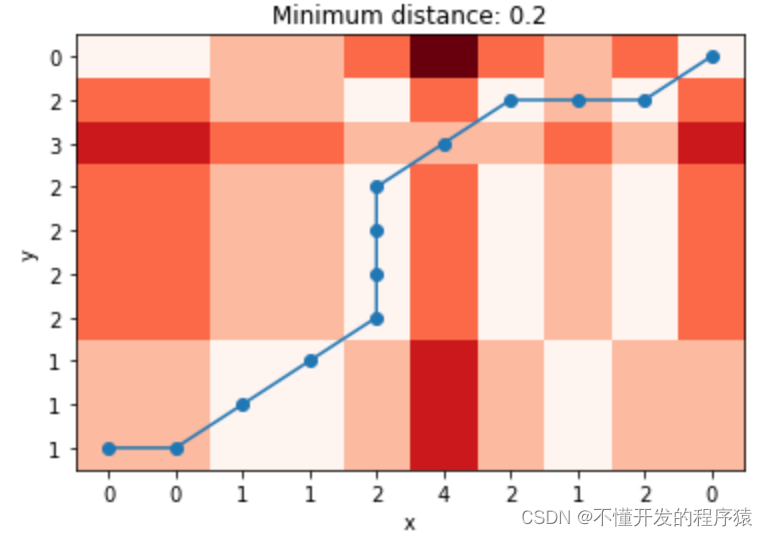
两个数组并不一致，其距离为0.2，符合我们的预期。

接下来我们尝试使用两个直觉上，差距更大的数组进行观察。

x = [0, 0, 1, 1, 2, 4, 2, 1, 2, 0]
y = [9, 9, -6, -8, 7, -3, 8, 1, 9, -9]

dist, cost, acc, path = dtw(x, y, dist_fun)

plt_distance(dist, cost, acc, path)

在这里，我们造了两个看起来完全不同的两个数组，它们之间的距离是3.25，远高于上一个距离0.2。这也符合我们的直观认知：

• 完全相同的数组，距离为0
• 有拉长或缩短的两个数组，距离为0
• 完全不同的数组，距离大于0
• 直觉上相差越大的数组，距离相差越大

接下来我们使用同样的方法，对二维数组之间的距离进行观察。

2、衡量二维数组之间的距离

首先，创造两个二维数组，二维数组对应了空间中的点，因此我们可以使用欧氏距离进行度量

from sklearn.metrics.pairwise import euclidean_distances
x = [[0, 0], [0, 1], [1, 1], [1, 2], [2, 2], [4, 3], [2, 3], [1, 1], [2, 2], [0, 1]]
y = [[1, 0], [1, 1], [1, 1], [2, 1], [4, 3], [4, 3], [2, 3], [3, 1], [1, 2], [1, 0]]
dist_fun = euclidean_distances

dist, cost, acc, path = dtw(x, y, dist_fun)
plt_distance(dist, cost, acc, path)

从以上示例可以看出，DTW可以用于计算两个二维数组之间的距离。如果你感兴趣，可以自己尝试变换数组，观察DTW计算的距离，是否符合我们刚刚总结出来的四条规律。

DTW不仅可以用于衡量一、二维数组，实际上，任何能够定义距离的数据，都可以使用DTW方法进行计算，例如字符串。

3、衡量一维字符串之间的距离

首先定义两个字符串，在这里，我们将使用字符串之间的距离度量方法edit_distance

from nltk.metrics.distance import edit_distance
x = ['i', 'soon', 'found', 'myself', 'muttering', 'to', 'the', 'walls']
y = ['see', 'drown', 'himself']
dist_fun = edit_distance

dist, cost, acc, path = dtw(x, y, dist_fun)
plt_distance(dist, cost, acc, path)

DTW成功计算了两个句子之间的距离是0.727，如果你感兴趣，可以尝试变换不同的词语。

4、衡量声音之间的距离

通常来说，我们并不会将声音读取数据直接用于计算距离，因为声音数据样本点较多，计算起来比较慢，同时影响因素也比较多，例如噪声等。

通常都是将声音数据进行特征提取，然后对提取的特征进行距离度量，接下来的实验中，我们将使提取两段声音的MFCC特征，然后使用DTW计算距离。

import librosa

# 命令“a”
y1, sr1 = librosa.load('/home/jovyan/datas/train/fcmc0-a1-t.wav')
# 命令“b”
y2, sr2 = librosa.load('/home/jovyan/datas/train/fcmc0-b1-t.wav')

为了确保我们正确加载了音频，接下来将播放这两个音频。

from IPython import display

display.Audio(y1,rate=sr1)

display.Audio(y2,rate=sr2)

然后提取两个音频的MFCC特征。

mfcc1 = librosa.feature.mfcc(y1, sr1)
mfcc2 = librosa.feature.mfcc(y2, sr2)

为了更好的理解MFCC，我们可以将其绘制出来，实际上，MFCC就是根据声音提取出来的一个矩阵，

from librosa import display

plt.subplot(1, 2, 1)
librosa.display.specshow(mfcc1)
plt.title('a')

plt.subplot(1, 2, 2)
display.specshow(mfcc2)
plt.title('b')

上图展示了根据声音计算的MFCC特征，本质其实就是一个声音的特征矩阵，因此绘制出来就是一个热力图的样子。

接下来我们使用DTW计算两个声音MFCC特征的距离

dist_fun=lambda m, n: np.linalg.norm(m - n, ord=1)
dist, cost, acc, path = dtw(mfcc1.T, mfcc2.T, dist_fun)
dist

25.370310163497926

可以看出，通过提取声音的MFCC特征，DTW可以用于度量两个声音的距离。

五、任务小结

本实验完成绘制热力图对不同类型数据之间的距离计算方法进行展示。通过本实验我们学习到了动态时间扭曲算法的相关知识，需要掌握以下知识点：

• 一维数组之间的距离
• 二维数组之间的距离
• 字符串之间的距离
• 声音之间的距离

经过实验，我们发现，对于类似发音正常和拖长的情况下，DTW算法能够很好的适应，并给出合理的距离。

–end–

说明

本实验（项目）/论文若有需要，请后台私信或【文末】个人微信公众号联系我