由数据范围反推算法复杂度以及算法内容 - AcWing
常用代码模板4——数学知识 - AcWing
基本思想:
首先,约数,又称因数。整数a除以整数b(b≠0)除得的商正好是整数而没有余数,我们就说a能被b整除,或b能整除a。a称为b的倍数,b称为a的约数。在这里我们讨论四个问题:
(一)求一个数的所有约数——试除法
暴力来解决这个问题很简单,就是从1开始遍历到n即可
for(int i = 1; i <= x; i++) { if(x % i == 0) res.push_back(i); }
时间复杂度为O(n),当处理m个数据时即为O(nm),所以当数据过多过大时时间效率较低,通过对质数的学习,我们知道一个数的因数即约数是成对出现的,所以我们同样可以用试除法,计算小的约数,并将大的约数添加到答案里,注意判断一下两者是否相同避免重复即可。
for(int i = 1; i <= x / i; i++) if(x % i == 0) { res.push_back(i); if(i != x/i) res.push_back(x/i); }
869. 试除法求约数 - AcWing题库
给定 n 个正整数 ai,对于每个整数 ai,请你按照从小到大的顺序输出它的所有约数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个整数 ai。
输出格式
输出共 n 行,其中第 i 行输出第 i 个整数 ai 的所有约数。
数据范围
1≤n≤100,
2≤ai≤2×1e9
输入样例:
2
6
8
输出样例:
1 2 3 6
1 2 4 8 #include<iostream> #include<algorithm> #include<vector> using namespace std; int n; int main() { cin>>n; while(n--) { int x; cin >> x; vector<int> res; for(int i = 1; i <= x / i; i++) if(x % i == 0) { res.push_back(i); if(i != x/i) res.push_back(x/i); } sort(res.begin(), res.end()); for (auto k : res) cout << k << ' '; cout << endl; } return 0; }
(二)求一些数的乘积的约数个数
我们可以将一个数写成质因数的乘积的形式,也就是
那么这个数的约数个数就是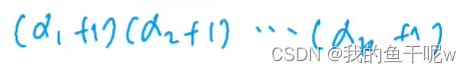
粗略的讲一下原理,就是我们可以将因数再分解,将因数的通式写出来,那么n的约数个数和我们β取法的个数是相同的,对于任意一个βi有0到αi个选择,即αi+1种,那么我们所有的选择方案就是将每个βi可选择的方案数累乘组合起来即可,也就得到了我们的约数个数的式子。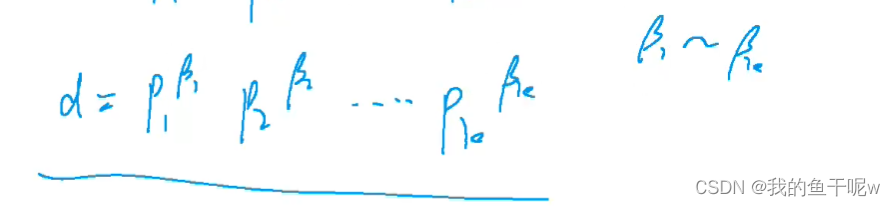
870. 约数个数 - AcWing题库
给定 n 个正整数 ai,请你输出这些数的乘积的约数个数,答案对 109+7 取模。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个整数 ai。
输出格式
输出一个整数,表示所给正整数的乘积的约数个数,答案需对 109+7 取模。
数据范围
1≤n≤100,
1≤ai≤2×1e9
输入样例:
3
2
6
8
输出样例:
12#include<iostream> #include<algorithm> #include<unordered_map> using namespace std; const int mod = 1e9 + 7; int n; int main() { cin>>n; unordered_map<int,int> primes; while(n--) { int x; cin>>x; for(int i = 2; i <= x / i; i++) { while(x % i == 0) { x /= i; primes[i]++; } } if(x > 1) primes[x]++; } long long res = 1; for(auto p : primes) res = res * (p.second + 1) % mod; cout << res; return 0; }
(三)一些数的乘积的约数之和
同样的,我们将N写成质因数乘积的形式,约数之和的式子就是

逆推想好想,我们将这个式子展开,每一个括号里我们都有ai+1种选择,那么我们一共就有
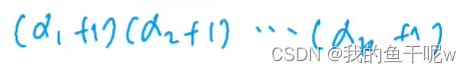
也就是上一个问题约数的个数的式子,对于分解后的每一个式子,它所选取的括号里的每一个p也是不同的,即分解后的每一个乘积式子都可以看作一个数,这样我们就将所有约数的和求出了。
871. 约数之和 - AcWing题库
给定 n 个正整数 ai,请你输出这些数的乘积的约数之和,答案对 109+7 取模。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个整数 ai。
输出格式
输出一个整数,表示所给正整数的乘积的约数之和,答案需对 109+7 取模。
数据范围
1≤n≤100,
1≤ai≤2×1e9
输入样例:
3
2
6
8
输出样例:
252#include<iostream> #include<algorithm> #include<vector> #include<unordered_map> using namespace std; typedef long long LL; const int mod = 1e9 + 7; int n; int main(){ cin>>n; unordered_map<int,int> primes; while(n--) { int x; cin>>x; for(int i = 2; i <= x / i; i++) { while(x % i == 0) { x /= i; primes[i]++; } } if(x > 1) primes[x]++;//x没除完 } LL res = 1; for (auto prime : primes) { LL p = prime.first, a = prime.second; LL t = 1; while (a--) t = (t * p + 1) % mod; //还要算0次方,算0次方就直接加1了,然后从一次方算方便些 /*计算一下: 第一步: t = (t * a + 1) t=p1的一次方+p1的零次方; 第二步: t = (t * a + 1) t=p1的二次方+p1的一次方+1=p1的二次方+p1的一次方+p1的零次方; */ res = res * t % mod; } cout << res; return 0; }
(四)最大公约数
这里我们用到欧几里得算法,也叫辗转相除法,d能整除a和b,那么d同样能整除ax+by,例如3能整除6和9,3也能整除15,21,24,如此,a和b的最大公约数也就是b和a mod b的最大公约数,因此,我们辗转相除,直至a mod b 为 0 返回即可。
对于a和b的最大公约数也就是b和a mod b的最大公约数的证明,a mod b可写作a - cb, (a, b) = (b, a - cb),我们反推,d能整除b和a - cb,那么d也能整除a - cb + xb,当x=c,a - cb + cb = a,即d也能整除a,所以是成立的。
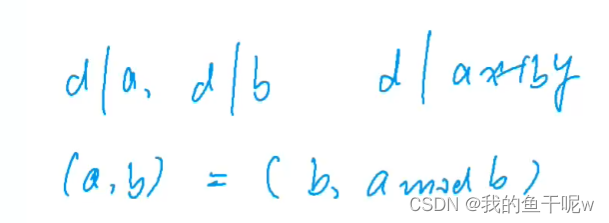
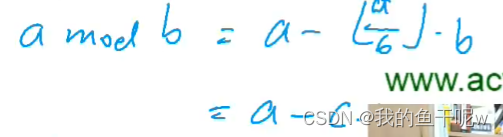
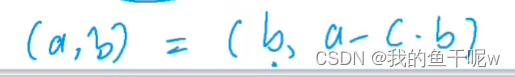
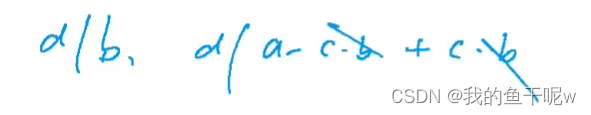
872. 最大公约数 - AcWing题库
给定 n 对正整数ai,bi,请你求出每对数的最大公约数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个整数对 ai,bi。
输出格式
输出共 n 行,每行输出一个整数对的最大公约数。
数据范围
1≤n≤1e5,
1≤ai,bi≤2×1e9
输入样例:
2
3 6
4 6
输出样例:
3
2#include<iostream> using namespace std; const int N=100010; int n; int gcd(int a,int b) { return b ? gcd(b, a % b) : a; } int main() { cin >> n; while(n--) { int a, b; cin >> a >> b; cout << gcd(a,b) << endl; } return 0; }