1. 深度学习和机器学习的主要区别在于对数据的处理, 机器学习主要通过算法直接进行推断, 而深度学习主要通过神经网络对各种算法进行加权, 然后汇总得出结论.
2. 常用的激活函数:
- tanh函数
- relu函数
- leaky relu函数
1.1 深度学习介绍
1.1.1 区别
-
机器学习的特征工程步骤是要靠手动完成的,而且需要大量领域专业知识
-
深度学习通常由多个层组成,它们通常将更简单的模型组合在一起,通过将数据从一层传递到另一层来构建更复杂的模型。通过大量数据的训练自动得到模型,不需要人工设计特征提取环节。
-
深度学习算法试图从数据中学习高级功能,这是深度学习的一个非常独特的部分。因此,减少了为每个问题开发新特征提取器的任务。适合用在难提取特征的图像、语音、自然语言领域(NLP)
1.1.2 深度学习应用场景 (眼睛/耳朵)
-
图像识别
-
物体识别
-
场景识别
-
车型识别
-
人脸检测跟踪
-
人脸关键点定位
-
人脸身份认证
-
-
自然语言处理技术
-
机器翻译
-
文本识别
-
聊天对话
-
-
语音技术
-
语音识别
-
1.1.3 深度学习代表算法-神经网络
人工神经网络( Artificial Neural Network, 简写为ANN)也简称为神经网络(NN)。是一种模仿生物神经网络(动物的中枢神经系统,特别是大脑)结构和功能的 计算模型。经典的神经网络结构包含三个层次的神经网络。分别输入层,输出层以及隐藏层。
其中每层的圆圈代表一个神经元,隐藏层和输出层的神经元有输入的数据计算后输出,输入层的神经元只是输入。
-
神经网络的特点
-
每个连接都有个权值,同一层神经元之间没有连接
-
神经元当中会含有激活函数
-
最后的输出结果对应的层也称之为全连接层
-
1.1.4 为什么深度学习现在效果非常好
过去十多年,得益于数字社会的发展,积累了大量的数据。以前的一些算法到达了瓶颈期,它们无法适用于大量的数据。"大规模"一直推动深度学习的发展进步。不仅仅是数据量的大,算法模型规模越来越大等。
-
数据
-
计算
-
训练网络需要GPU、TPU
-
-
算法
-
一些创新,如ReLU激活函数
-
1.2 神经网络基础
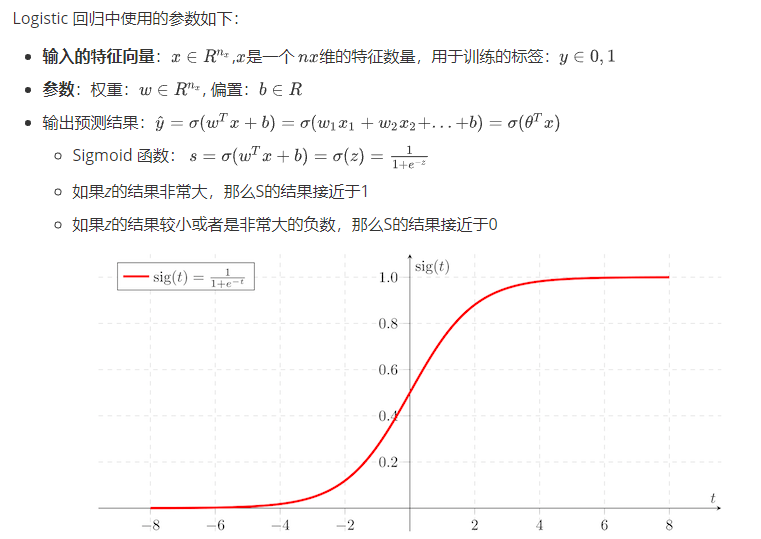
1.2.1 Logistic回归
逻辑回归是一个主要用于二分分类类的算法。那么逻辑回归是给定一个xx , 输出一个该样本属于1对应类别的预测概率, 得到的结果为0或1。

1.2.2 梯度下降算法
目的:使损失函数的值找到最小值.
方式:梯度下降.
函数的梯度(gradient)指出了函数的最陡增长方向。梯度的方向走,函数增长得就越快。那么按梯度的负方向走,函数值自然就降低得最快了。模型的训练目标即是寻找合适的 w 与 b 以最小化代价函数值。
1.2.3 向量化编程
每更新一次梯度时候,在训练期间我们会拥有m个样本,那么 这样每个样本提供进去都可以做一个梯度下降计算。所以我们要去做在所有样本上的计算结果、梯度等操作.
向量化的好处, 不用对每个特征都使用for循环, 速度更快.
1.3 浅层神经网络
1.3.1 浅层神经网络表示
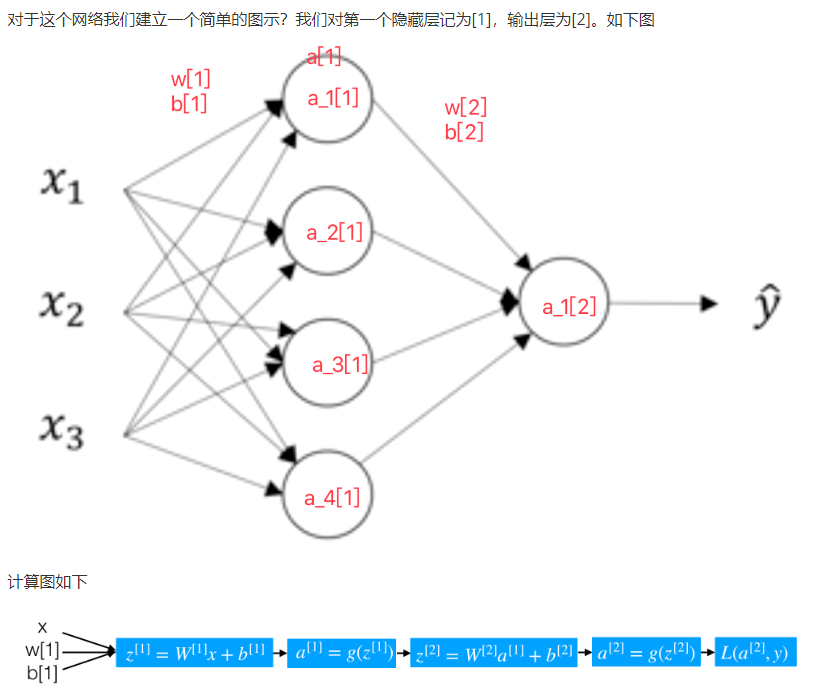
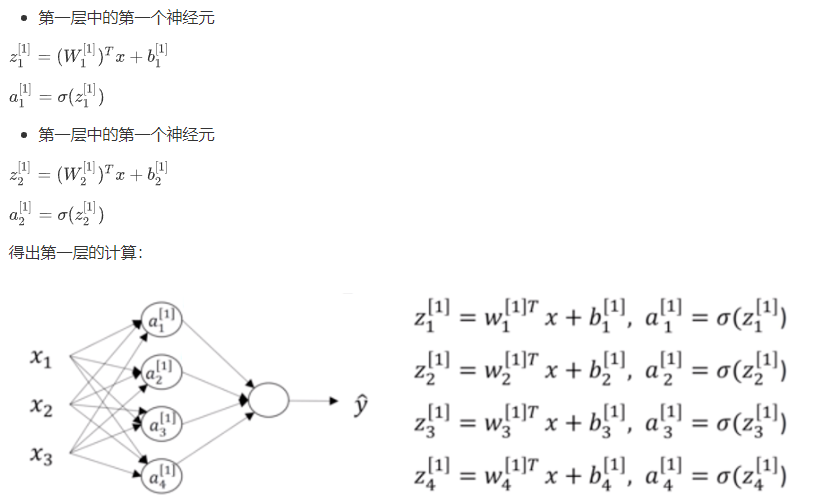
1.3.2 单个样本的向量化表示

1.3.3 激活函数的选择
涉及到网络的优化时候,会有不同的激活函数选择有一个问题是神经网络的隐藏层和输出单元用什么激活函数。之前我们都是选用 sigmoid 函数,但有时其他函数的效果会好得多,大多数通过实践得来,没有很好的解释性。
可供选用的激活函数有:
- tanh 函数(the hyperbolic tangent function,双曲正切函数) ,效果比 sigmoid 函数好,因为函数输出介于 -1 和 1 之间。 # 注 :tanh 函数存在和 sigmoid 函数一样的缺点:当 z 趋紧无穷大(或无穷小),导数的梯度(即函数的斜率)就趋紧于 0,这使得梯度算法的速度会减慢。
- ReLU 函数(the rectified linear unit,修正线性单元) # 当 z > 0 时,梯度始终为 1,从而提高神经网络基于梯度算法的运算速度,收敛速度远大于 sigmoid 和 tanh。然而当 z < 0 时,梯度一直为 0,但是实际的运用中,该缺陷的影响不是很大。
- Leaky ReLU(带泄漏的 ReLU) # Leaky ReLU 保证在 z < 0 的时候,梯度仍然不为 0。理论上来说,Leaky ReLU 有 ReLU 的所有优点,但在实际操作中没有证明总是好于 ReLU,因此不常用。
# 为什么需要非线性的激活函数
使用线性激活函数不使用激活函数、和直接使用 Logistic 回归没有区别,那么无论神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,就成了最原始的感知器了。
1.4 深层神经网络
1.4 深层神经网络
对于人脸识别等应用,神经网络的第一层从原始图片中提取人脸的轮廓和边缘,每个神经元学习到不同边缘的信息;网络的第二层将第一层学得的边缘信息组合起来,形成人脸的一些局部的特征,例如眼睛、嘴巴等;后面的几层逐步将上一层的特征组合起来,形成人脸的模样。随着神经网络层数的增加,特征也从原来的边缘逐步扩展为人脸的整体,由整体到局部,由简单到复杂。层数越多,那么模型学习的效果也就越精确。
通过例子可以看到,随着神经网络的深度加深,模型能学习到更加复杂的问题,功能也更加强大。
1.4.1 什么是深层网络?
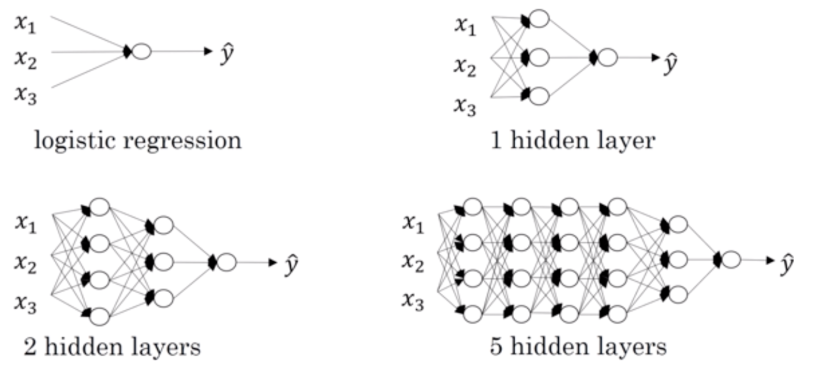
1.4.2 四层网络的前向传播与反向传播
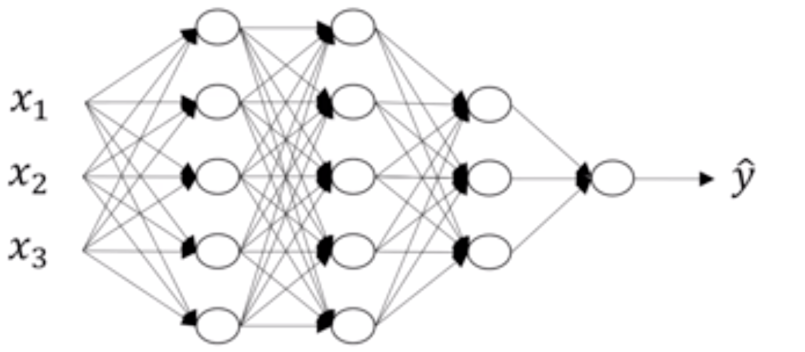
在这里首先对每层的符号进行一个确定,我们设置L为第几层,n为每一层的个数,L=[L1,L2,L3,L4],n=[5,5,3,1]
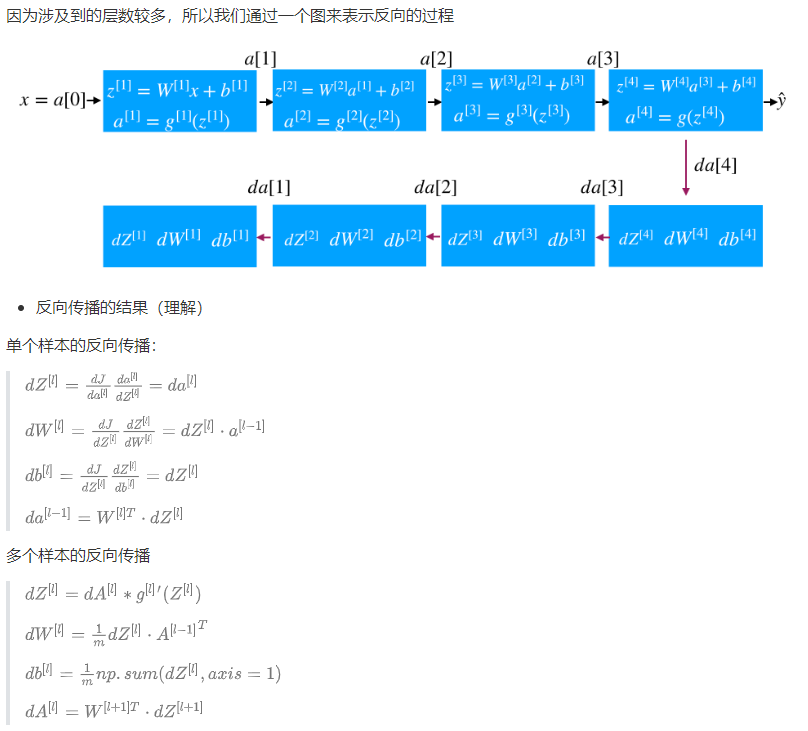
1.4.2.1 前向传播

1.4.2.2 反向传播
1.4.3 参数与超参数
参数即是我们在过程中想要模型学习到的信息(模型自己能计算出来的),例如W[l]W[l],b[l]b[l]。而超参数(hyper parameters)即为控制参数的输出值的一些网络信息(需要人经验判断)。超参数的改变会导致最终得到的参数 W[l],b[l] 的改变。
典型的超参数有:
-
学习速率:α
-
迭代次数:N
-
隐藏层的层数:L
-
每一层的神经元个数:n[1],n[2],...
-
激活函数 g(z) 的选择
当开发新应用时,预先很难准确知道超参数的最优值应该是什么。因此,通常需要尝试很多不同的值。应用深度学习领域是一个很大程度基于经验的过程。
参数初始化 :
-
为什么要随机初始化权重.
如果在初始时将两个隐藏神经元的参数设置为相同的大小,那么两个隐藏神经元对输出单元的影响也是相同的,通过反向梯度下降去进行计算的时候,会得到同样的梯度大小,所以在经过多次迭代后,两个隐藏层单位仍然是对称的。无论设置多少个隐藏单元,其最终的影响都是相同的,那么多个隐藏神经元就没有了意义。
在初始化的时候,W 参数要进行随机初始化,不可以设置为 0。b 因为不存在上述问题,可以设置为 0。
-
初始化权重的值选择
这里将 W 的值乘以 0.01(或者其他的常数值)的原因是为了使得权重 W 初始化为较小的值,这是因为使用 sigmoid 函数或者 tanh 函数作为激活函数时,W 比较小,则 Z=WX+b 所得的值趋近于 0,梯度较大,能够提高算法的更新速度。而如果 W 设置的太大的话,得到的梯度较小,训练过程因此会变得很慢。
ReLU 和 Leaky ReLU 作为激活函数时不存在这种问题,因为在大于 0 的时候,梯度均为 1。