系列文章目录
目录
- 系列文章目录
- 62.不同路径
- ①回溯算法(超时)
- ②深度搜索(超时)
- ③动态规划
- 63. 不同路径 II
- 动态规划
62.不同路径
①回溯算法(超时)
本质是穷举。
class Solution {
int[] chose = new int[2];
int col = 1;
int row = 1;
int res = 0;
public int uniquePaths(int m, int n) {
backTracking(m,n);
return res;
}
public void backTracking(int m, int n) {
//终止条件
if (row > m || col > n) return;//越界
if(row == m && col == n){
res++;
return;
}
for (int i = 0; i < chose.length; i++) {
if (i == 0) {//向下
row++;
} else {//向右
col++;
}
backTracking(m,n);
//回溯
if (i == 0) {//向下
row--;
} else {//向右
col--;
}
}
}
}
②深度搜索(超时)
用图论里的深搜,来枚举出来有多少种路径。
题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
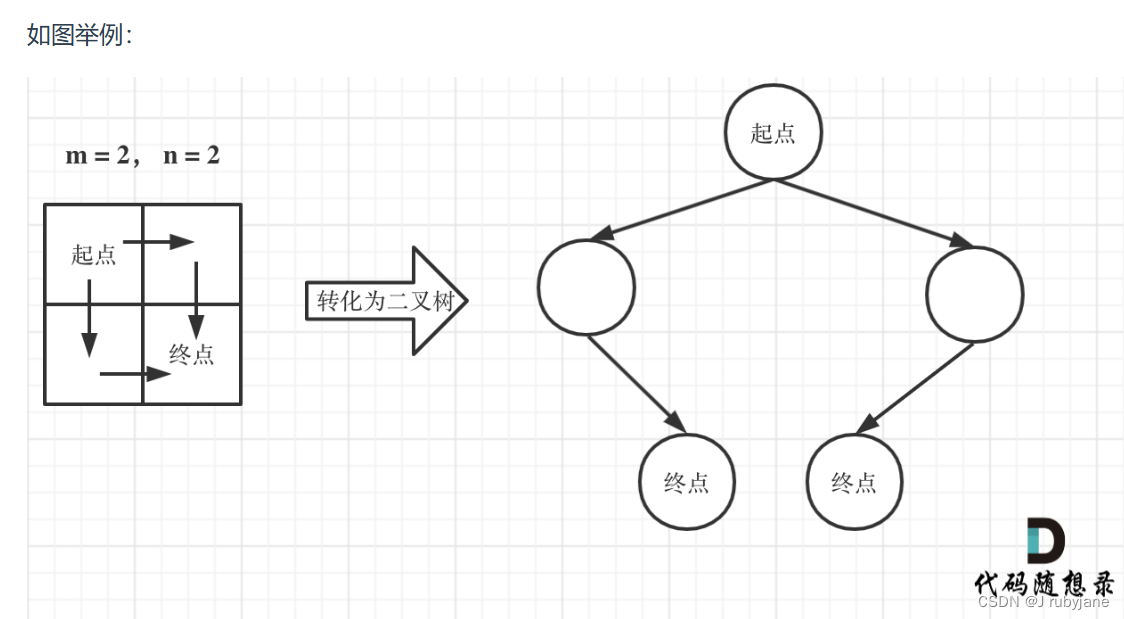
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
class Solution {
public int uniquePaths(int m, int n) {
return dfs(1, 1, m, n);
}
public int dfs(int row, int col, int m, int n) {
if (row > m || col > n) return 0;// 越界了
if (row == m && col == n) return 1;// 找到一种方法,相当于找到了叶子节点
return dfs(row + 1, col, m, n) + dfs(row, col + 1, m, n);
}
}

③动态规划
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
动规五部曲:
- 确定
dp数组(dp table)以及下标的含义:dp[i][j]表示从(0 ,0)出发,到(i, j)有dp[i][j]条不同的路径。 - 确定递推公式:想要求
dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j]和dp[i][j - 1]。所以dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。 dp数组的初始化:dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。- 确定遍历顺序:这里要看一下递推公式
dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。这样就可以保证推导dp[i][j]的时候,dp[i - 1][j]和dp[i][j - 1]一定是有数值的。 - 举例推导
dp数组。
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {//行
for (int j = 0; j < n; j++) {//列
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
}
}

63. 不同路径 II
动态规划
动规五部曲:
- 确定
dp数组(dp table)以及下标的含义:dp[i][j]表示从(0 ,0)出发,到(i, j)有dp[i][j]条不同的路径。 - 确定递推公式:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。 dp数组如何初始化:因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i][0]一定为1,dp[0][j]也同理。但如果(i, 0)这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。故代码里for循环的终止条件是,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理。- 确定遍历顺序:从递归公式
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j]和dp[i][j - 1]一定是有数值。 - 举例推导
dp数组。
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
//初始化
//如果在起点或终点遇到障碍物,直接返回0
if (obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1) return 0;
/* for (int i = 0; i < m; i++) {//每行第一个元素
// 如果第一行某个格子出现障碍物,则当前格子以及右边的所有格子都无法到达(直接使用初始化的默认值0即可)
if (obstacleGrid[i][0] == 1) {
break;
}
// 如果当前格子没有障碍物
dp[i][0] = 1;
}
for (int i = 0; i < n; i++) {//每列第一个元素
// 如果第一列某个格子出现障碍物,则当前格子以及下边的所有格子都无法到达(直接使用初始化的默认值0即可)
if (obstacleGrid[0][i] == 1) {
break;
}
// 如果当前格子没有障碍物
dp[0][i] = 1;
}*/
//for循环的终止条件,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;//每行第一个元素
for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) dp[0][i] = 1;//每列第一个元素
for (int i = 1; i < m; i++) {//每行
for (int j = 1; j < n; j++) {//每列
/*if (obstacleGrid[i][j] == 1) {
dp[i][j] = 0;
} else {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}*/
if (obstacleGrid[i][j] == 0) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
}
}