一、KMP算法简介

KMP算法是一种改进的字符串匹配算法，由 D.E.Knuth ，J.H.Morris 和 V.R.Pratt 提出的，因此人们称它为克努特 — 莫里斯 — 普拉特操作（简称 KMP 算法）。 KMP 算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个 next() 函数实现，函数本身包含了模式串的局部匹配信息。 KMP 算
法的时间复杂度 O(m+n) [1] 。来自 ------- 百度百科。（这里应该是next数组，通过函数获取到next数组）

二、KMP算法的详细图解

1. 先了解BF算法的基本思路

在了解KMP算法之前，我们先来了理解BF算法的原理。

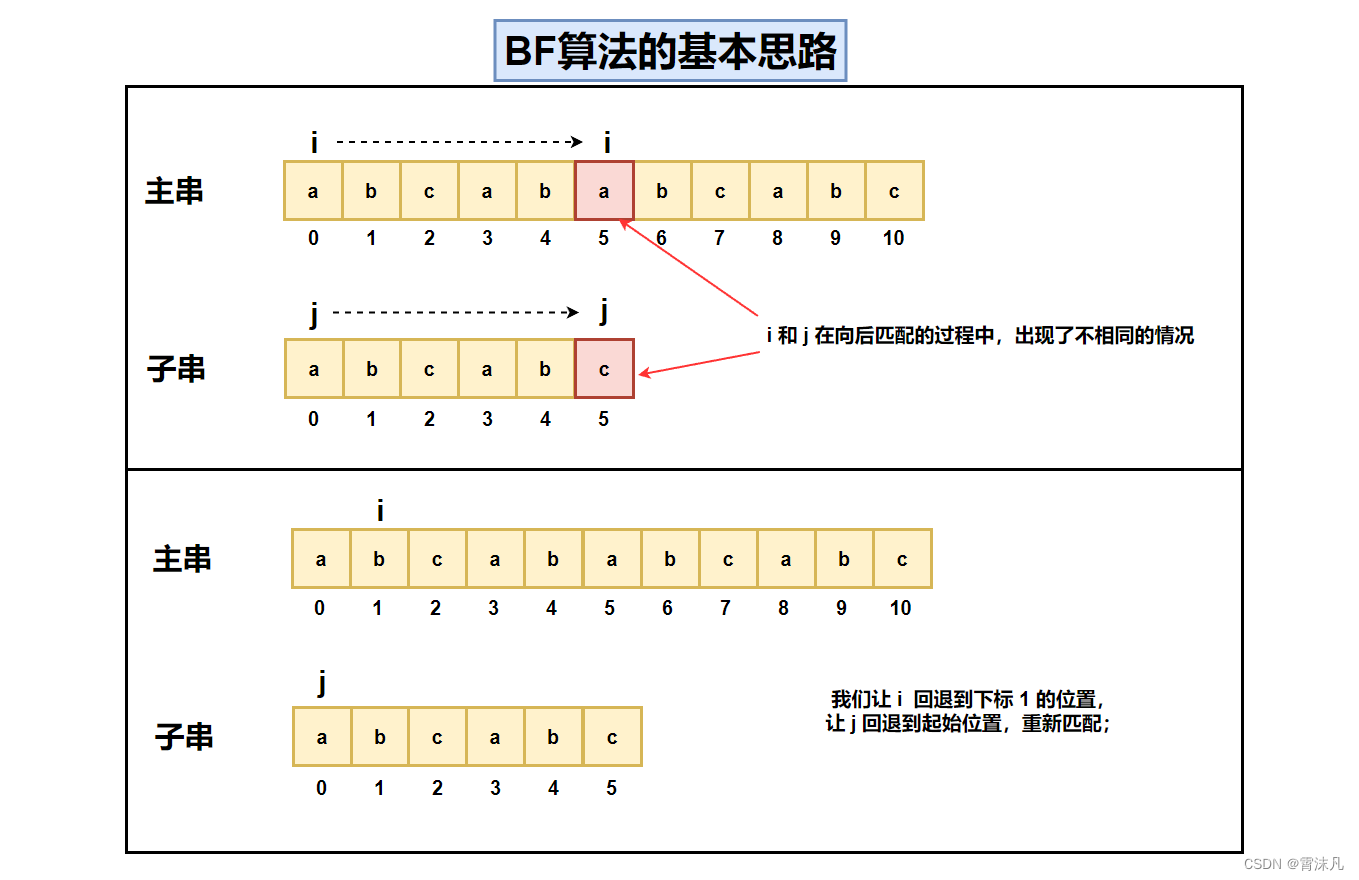
BF算法，即暴力(Brute Force)算法，是普通的模式匹配算法，BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符;若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。BF算法是一种蛮力算法。

代码如下：

int strStr(string haystack, string needle) {
    int n = haystack.size();
    int m = needle.size();
    for (int i = 0; i <= n - m; i++) {// i 每次回退到前一个位置的下一个位置
        bool flag = 1;
        for (int j = 0; j < m; j++) { // j 每次匹配失败后回退到0号位置
            if (haystack[i + j] != needle[j]) {
                flag = 0;
                break;
            }
        }
        if (flag) {
            return i;
        }
    }
    return -1;
}

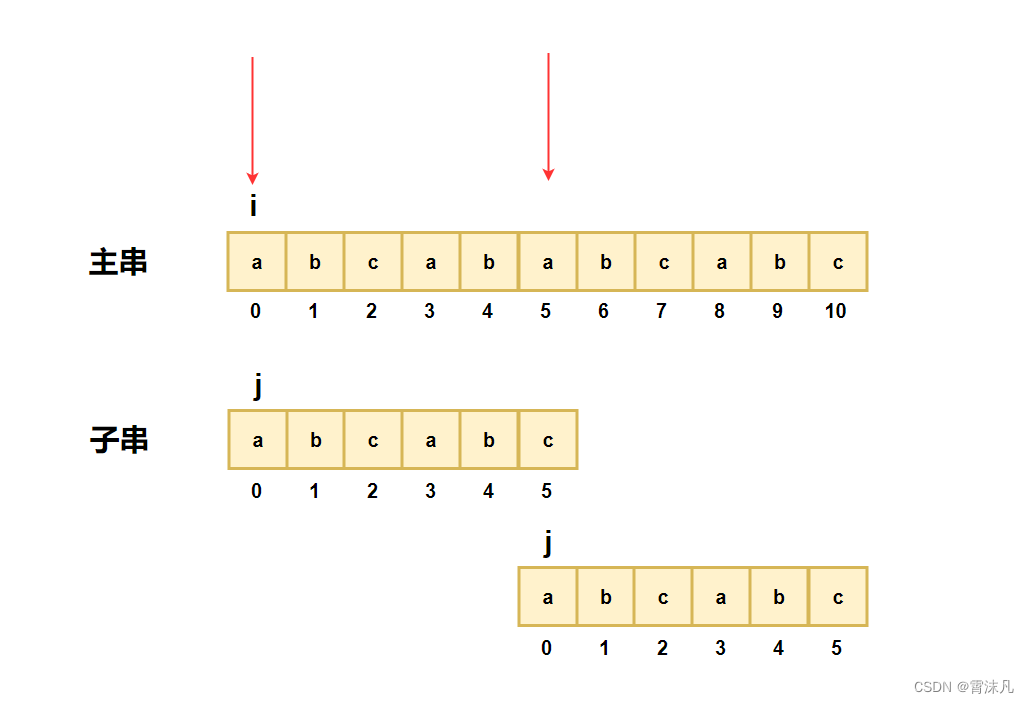
其中i < n - m; 的原因，如下图所示：当 i 走到下标5的位置时，剩下的子串（包括其本身）是符合子串的长度的，但是当 i 走到下标6的位置时，就没有足够的数量去匹配子串；

2. 简单了解KMP算法

接下来我们来看一下KMP算法：

如下图所示：如果按照BF算法，i 回退到下标1的位置，j 回退到下标0的位置，但是它们的字符并不相等，而且之前都匹配成功了5个字符，这样的操作显得有些多余；
KMP算法和BF算法的本质区别是：主串的 i 并不会回退，并且子串 j 也不会回退到 0 号位置；而是回退到一个特定的位置。

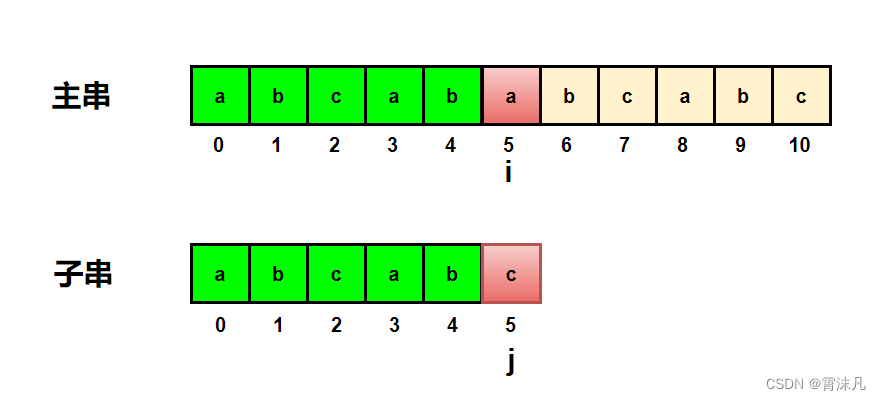
那么这个特定的位置到底是哪个位置呢？

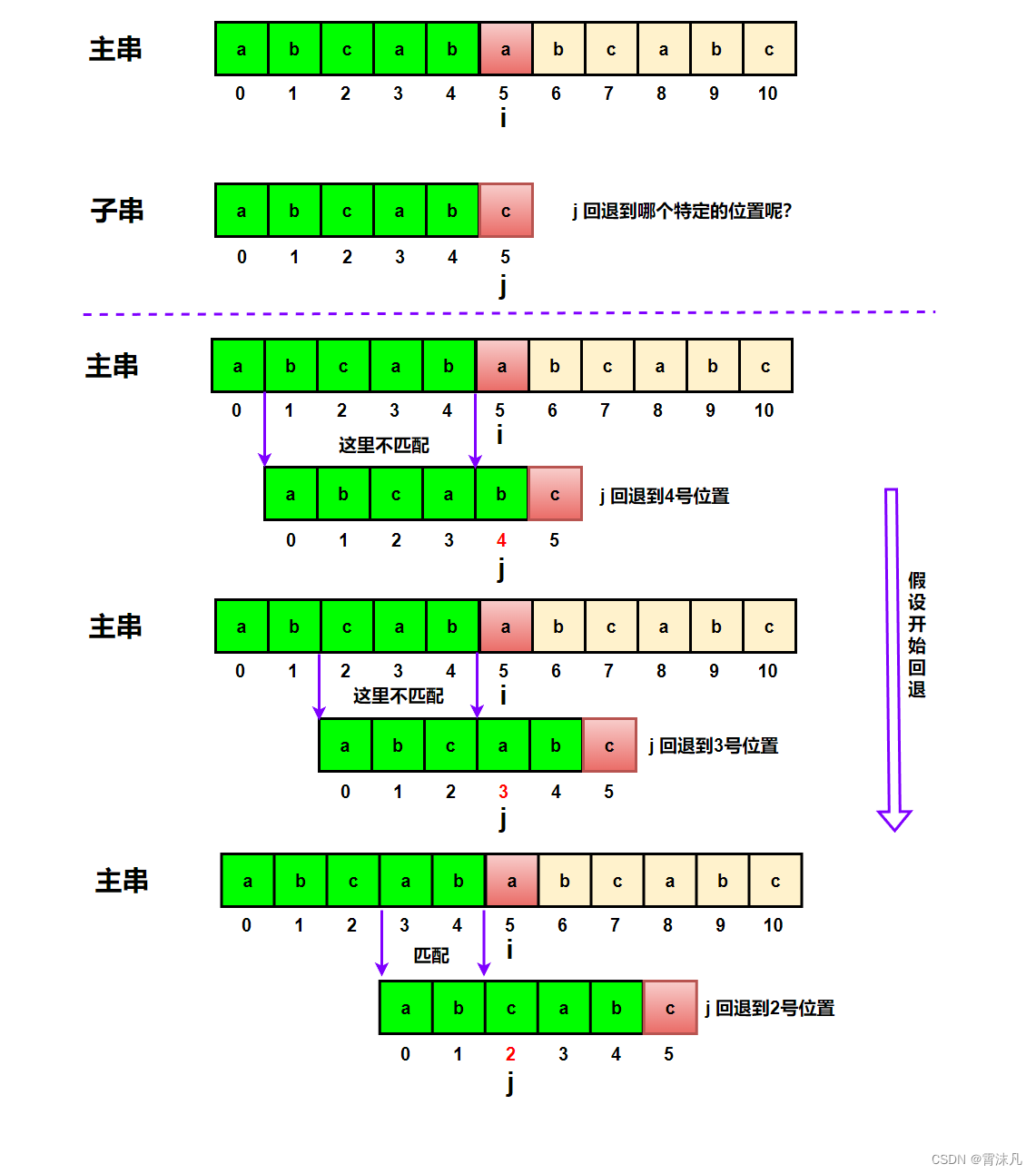
从上个图可以看到，当 j 回退到2号位置时，子串能够最大程度上在冲突位置之前匹配主串。

但是我们发现，当 j 回退到2号位置时，i 和 j 所对应的字符并不相同，此时我们的 j 还是需要回退的，这个我们到后面讲，但是你想一下，如果 j 回退到2号位置时，刚好 i 和 j 所对应的字符相同，那么我们的回退就是很成功的。（乍一听是这么个到道理，我们再继续往下看）

刚刚 j 回退到2号位置，我们知道了为什么要回退的原因，那么这个2号位置怎么求出来，更是我们所关心的。如何求呢?（先不要着急，KMP算法还是比较抽象的，先看看图解）

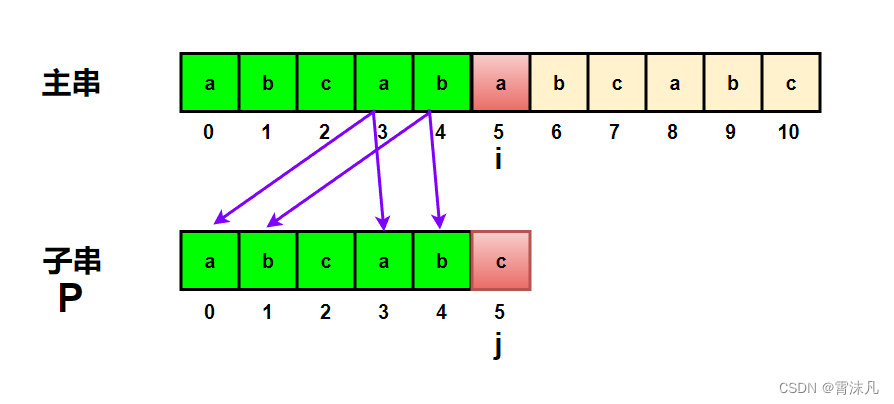
从图中我们可以发现，5号位置是发生冲突的位置，在5号位置之前，主串的【3】【4】下标和子串【3】【4】下标都是a、b；（这不是废话吗？要是不相同i 和 j 怎么可能走到5呢！！）并且子串的【0】【1】下标也是a、b；它们的长度是不是2啊，j 就回退到2；（可能有人会觉得这是什么逻辑或者说你这不是凑巧吗？）我们就以这种例子看，到后面你就不会这么觉得了；（这里没理解明白的，没关系，直接向下看）

3. next数组的引入

next数组的作用：保存字串某个位置失败后要回退的哪个位置。

KMP 的精髓就是 next 数组：也就是用 next [ j ] = k;来表示，不同的 j 来对应一个 k值，这个 k 就是你将来要将 j 移动到哪个位置。而 k 的值是这样求的：

规则：找到匹配成功部分的两个相等的真子串（不包含本身），一个以下标 0 字符开始，另一个以 j-1 下标字符结尾。
不管什么数据 next [0] = -1;next [1] = 0；

这里听完，或许你还不知道怎么算next数组，接下来我们做两组练习

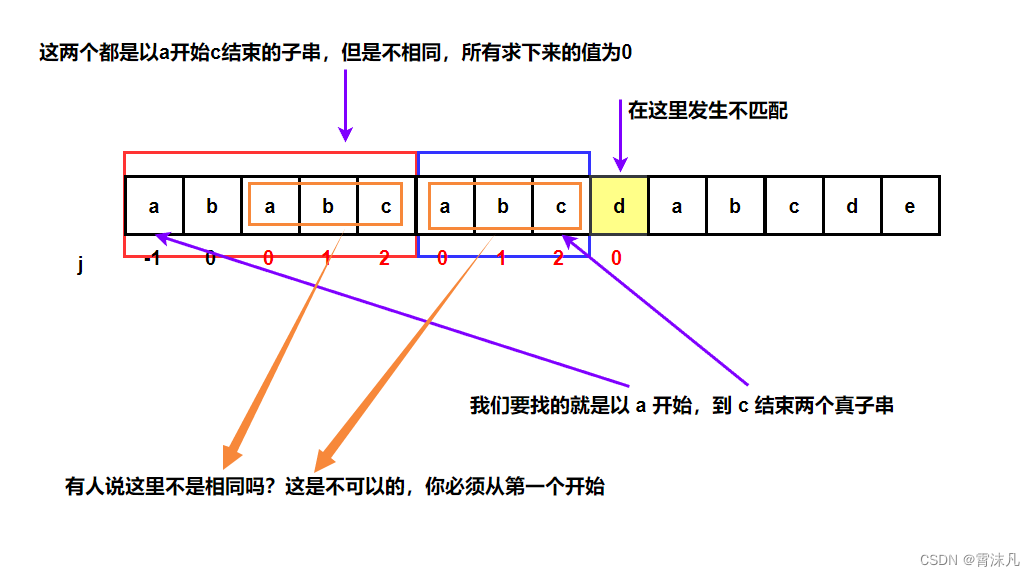
求解next数组：对于子串”ababcabcdabcde”，求其的 next 数组？

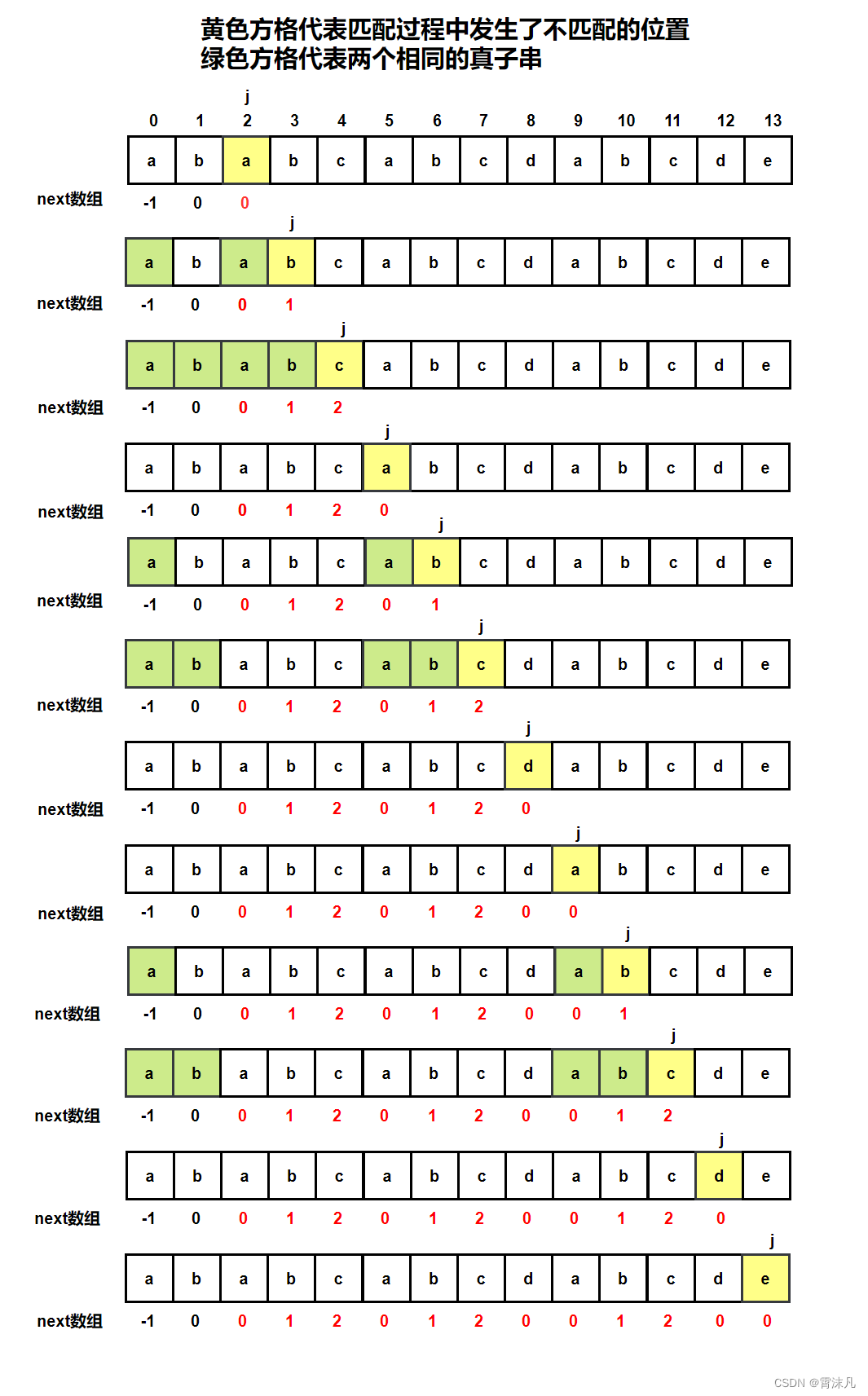
说明一下：

在图中字符数组下面的下标表示所求的next数组对应的内容，表明发生匹配失败时需要回退到哪个下标（也就是回退到字符数组上方对应的下标）
在求next数组的时候，你必须保证，在发生不匹配时，之前匹配成功过的字符中，要存在两个相同的真子串，并且这两个真子串是一个从下标0开始，一个从以标 j - 1 结尾；下面这种情况是不可以的

注：对于上面的next数组为什么从-1开始，第二个是0；有些人喜欢从0开始，有些喜欢从-1开始，如果 j 回退到-1，那么 j++ 就到了子串下标0的位置，如果是 j 回退到0，那么就刚好；至于第二个给0，其实也能够给想到，当你在第二个位置发生不匹配时，前面肯定找不到两个相同的真子串。

我相信大家对上面的next数组如何求解应该问题不大。这里再提供一个练习，看看自己有没有掌握；

对于子串”abcabcabcabcdabcde”，求其的 next 数组？

答案：-1,0,0,0,1,2,3,4,5,6,7,8,9,0,1,2,3,0

--------------------------------------------------------------------------------------------------------------------------------

紧接着又有一个问题出现了，我们虽然通过画图可以计算到next数组，但是如何用代码实现出来，是我们最关心的。这里需要用到公式推导，接下来看下图的推导过程。

总结：

首先假设： next[ i ] = k 成立，那么，就有这个式子成立：
P[0]...P[k-1] = P[x]...P[i-1];得到： P[0]...P[k-1] = P[i-k]..P[i-1];
到这一步：我们再假设如果 P[k] = P[i];
我们可以得到 P[0]...P[k] = P[i-k]..P[i];那这个就是 next[i+1] = k+1;

4. next数组的代码实现（含动态演示）

void getNext(int* next, const string& s) {
    int len = s.size();
    next[0] = -1;
    if (len == 1) return;
    next[1] = 0;
    int k = 0;//前一项的K
    int i = 2;//此时i表示当前下标，也就是下一项
    while (i < len) {
        if (k == -1 || s[i - 1] == s[k]) 
        {
            next[i] = k + 1;
            k++;
            i++; 
        }
        else {
            k = next[k];
        }
    }
}

next数组动态演示：

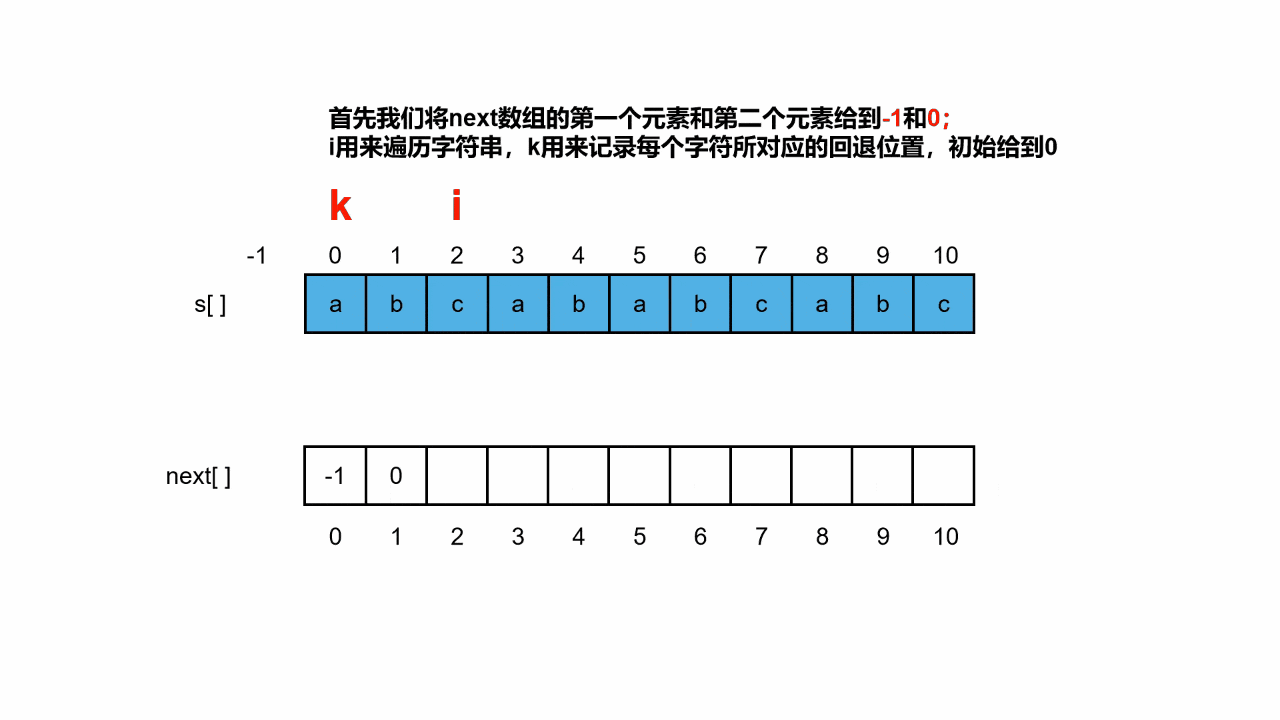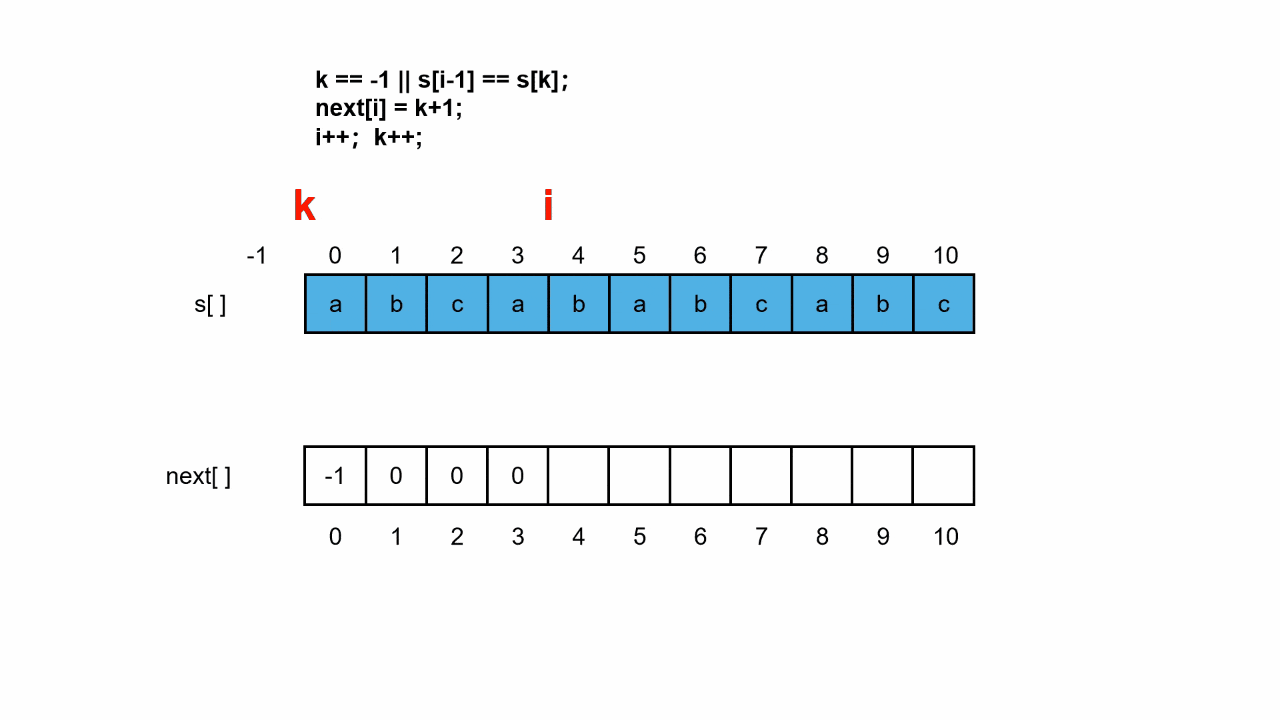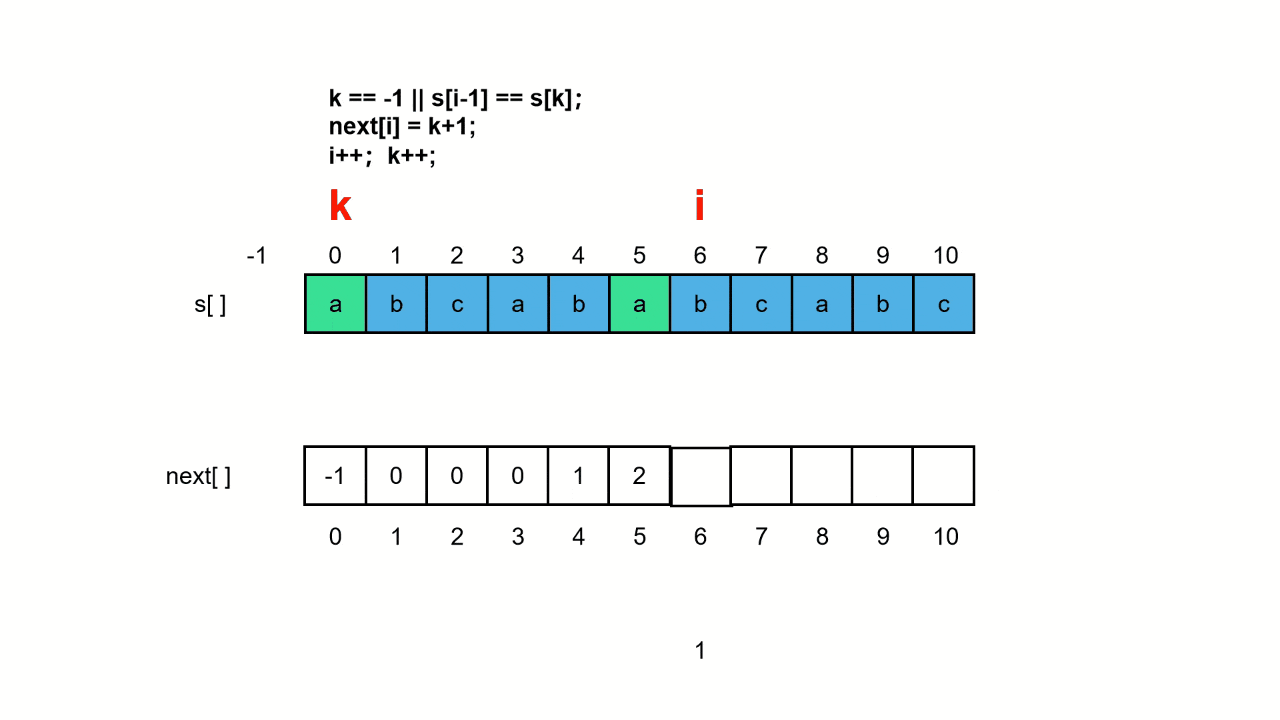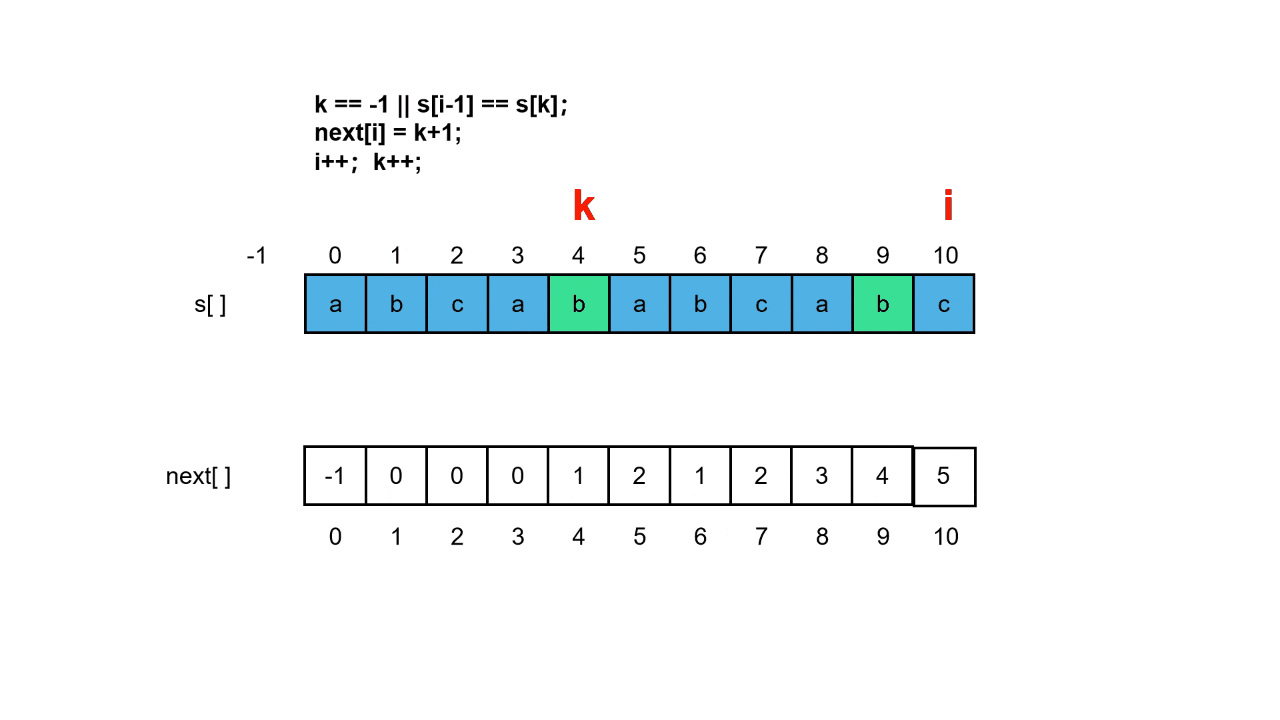
三、KMP算法完整代码

class Solution {
public:
    void GetNext(int* next, const string& s) {
        int len = s.size();
        next[0] = -1; //next数组第一个元素直接给-1
        if (len == 1)return;//如果传过来的子串只有一个字符，我们直接返回，因为next数组已经给定了
        next[1] = 0;  //next数组第二个元素直接给0
        int k = 0; //前一项的K
        int i = 2; //此时i表示当前下标，也就是下一项
        while (i < len) {
            if (k == -1 || s[i - 1] == s[k]) 
            {
                next[i] = k + 1;
                k++;
                i++; 
            }
            else {
                k = next[k];
            }
        }
    }

    int strStr(string haystack, string needle) {
        int len1=haystack.size(); //计算出主串的长度
        int len2=needle.size();   //计算出子串的长度

        if(len1 == 0 && len2 != 0) return -1; 
        if(len1 == 0 && len2 == 0) return 0;  
        if(len1 != 0 && len2 == 0) return 0;
  
        int i = 0;//遍历主串
        int j = 0;//遍历字串

        int *next = new int[len2];//开辟一个next数组，空间大小是子串的大小
        GetNext(next, needle); //获取子串的next数组

        while(i < len1 && j < len2)
        {
            //如果主串和子串的字符相同或者j回退到了-1位置，我们都要把i和j进行++
            if((j == -1) || haystack[i] == needle[j])
            {
                i++;
                j++;
            }
            else    
            {
                j = next[j];//主串和子串的字符不匹配，j需要依靠next数组进行回退操作
            }
        }
        
        if(j >= len2) return i - j;//子串遍历完了
        else return -1;//子串没有遍历完了
    }
};