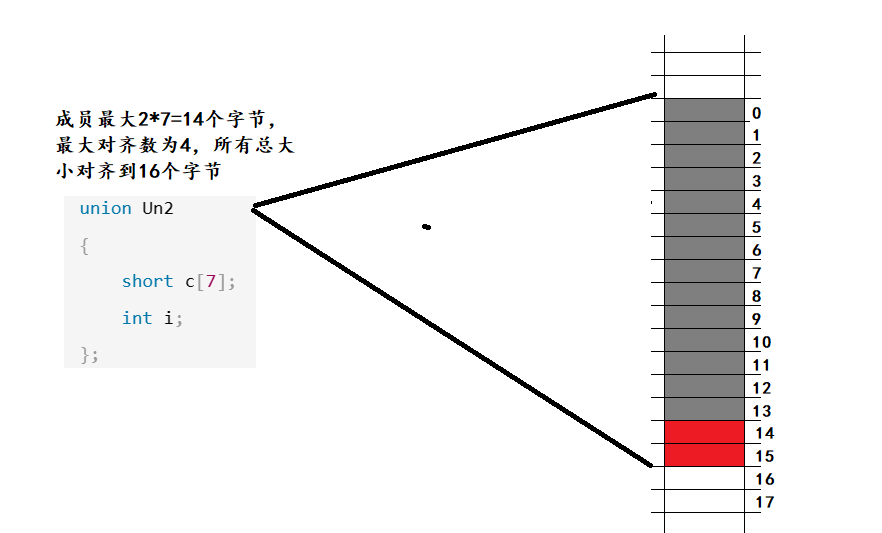
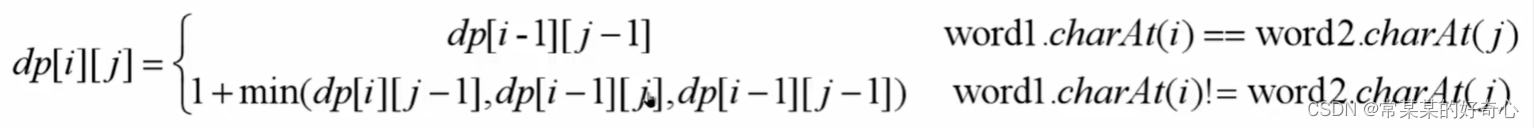数据规模->时间复杂度

<=10^4 😮(n^2)
<=10^7:o(nlogn)
<=10^8:o(n)
10^8<=:o(logn),o(1)

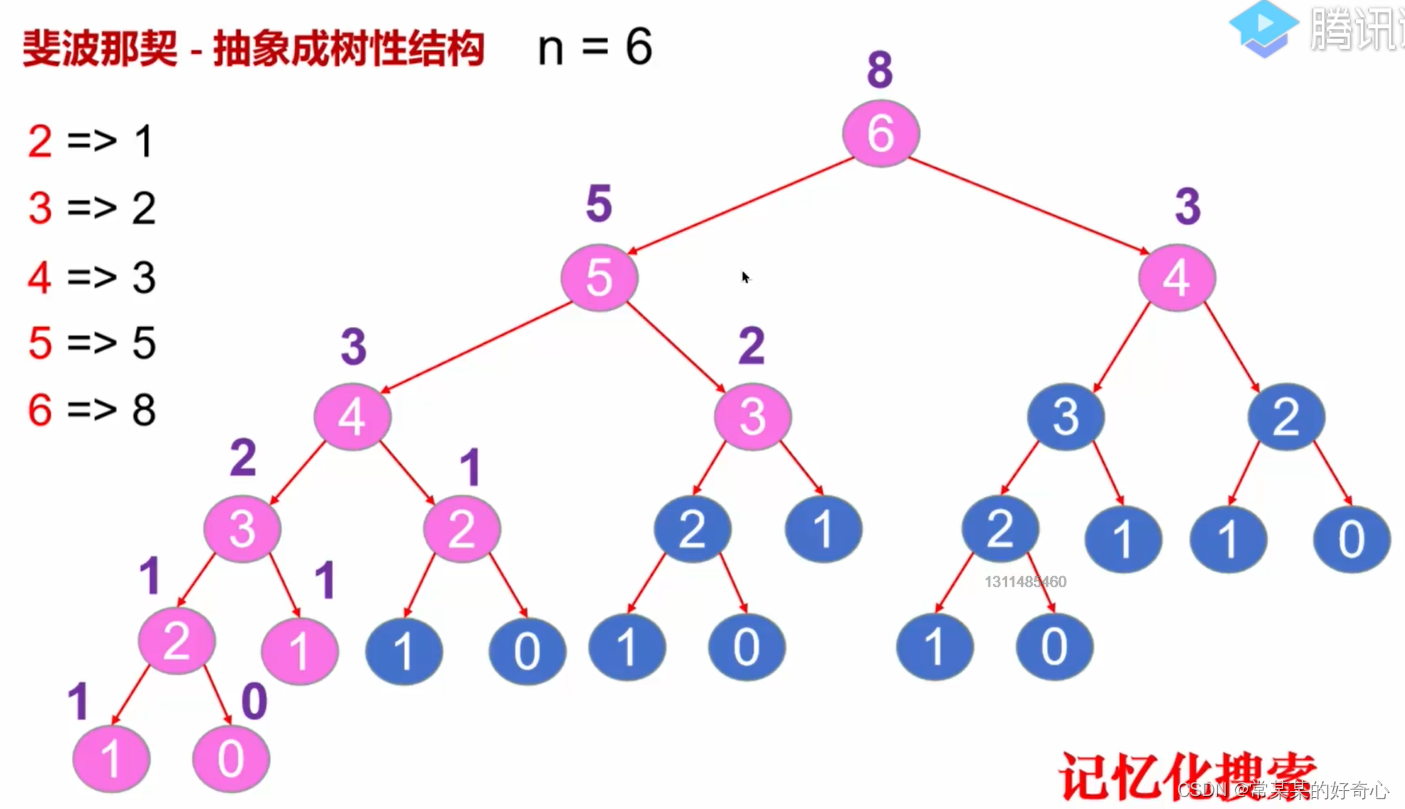
lc 509【剑指 10-1】：斐波那契数列问题 - 动态规划入门
https://leetcode.cn/problems/fibonacci-number/
提示：
0 <= n <= 30

#方案一：DFS+记忆化搜索hashmap/list)
class Solution:   
    def fib(self, n: int) -> int:
        memo=[-1]*(n+1)
        # 
        def fib_cur(n):
            if n==0:return 0
            if n==1:return 1
            if memo[n]!=-1:return memo[n]
            #
            memo[n]=fib_cur(n-1)+fib_cur(n-2)
            return memo[n]
        #
        return fib_cur(n)
        

#方案二：DP(o(n),o(n))
class Solution:   
    def fib(self, n: int) -> int:
        if n<=1:return n
        #状态数组
        memo=[-1]*(n+1)
        #状态初始
        memo[0],memo[1]=0,1
        #状态转移
        for i in range(2,n+1):
            memo[i]=memo[i-1]+memo[i-2]
        #终态
        return memo[n]
             
#方案三：DP+状态压缩（o(1),o(n)）
class Solution:   
    def fib(self, n: int) -> int:
        if n<=1:return n
        #状态初始(状态数组空间压缩，终态只和前两个状态有关)
        prev,curr=0,1
        #状态转移
        for i in range(2,n+1):
            prev,curr=curr,prev+curr
        #终态值
        return curr

lc 322【剑指 103】：零钱兑换
https://leetcode.cn/problems/coin-change/
提示：
1 <= coins.length <= 12
1 <= coins[i] <= 2^31 - 1
0 <= amount <= 10^4

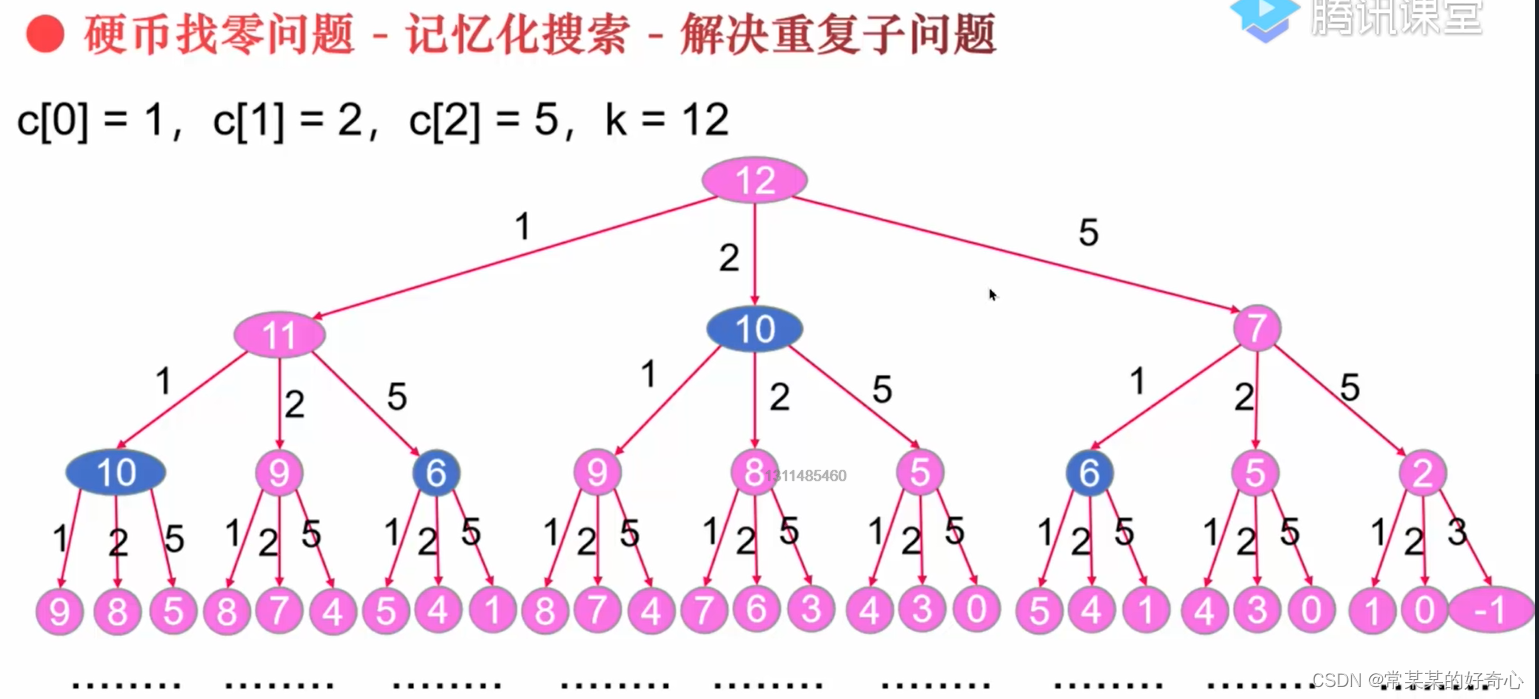
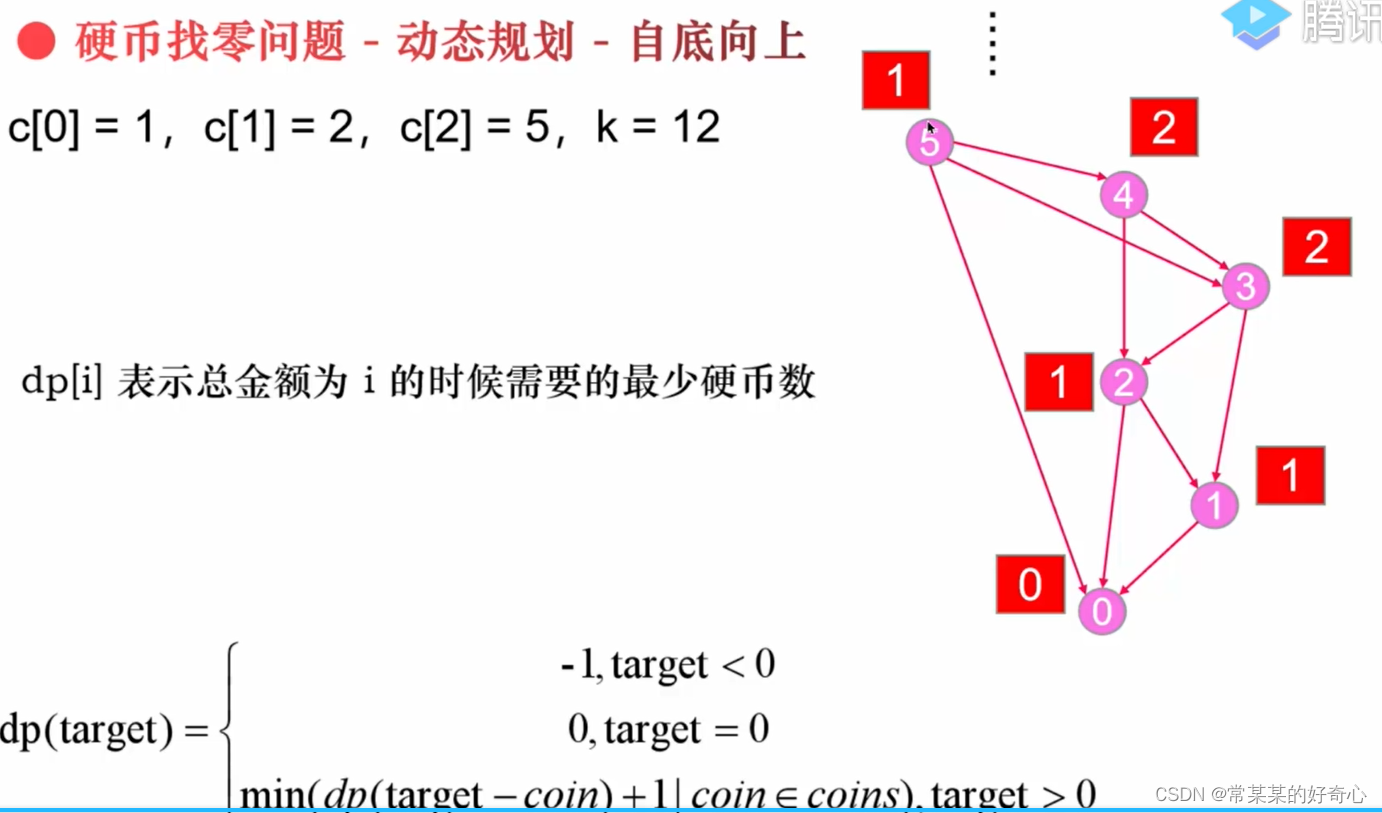
在这里插入图片描述

#方案一：回溯(超时)
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        def dfs(target,c):
            if target==0:return 0
            #
            mincoins=float('inf')
            for i in range(len(c)):
                if target-c[i]<0:continue #剪枝1(留根节点值>=0)
                #
                submincoins=dfs(target-c[i],c)
                if submincoins==-1:continue #剪枝2(不纳入计算)
                mincoins=min(mincoins,submincoins+1)#"各路选最优"
            #"左-右-根"
            return -1 if mincoins==float('inf') else mincoins

        return dfs(amount,coins)

#方案二：回溯+记忆化搜索
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        memo=[float('inf')]*(amount+1)
        def dfs(target,c):
            if target==0:return 0
            if memo[target]!=float('inf'):return memo[target]#key:存每个target的mincoins
            #
            mincoins=float('inf')
            for i in range(len(c)):
                if target-c[i]<0:continue #剪枝1(留根节点值>=0)
                #
                submincoins=dfs(target-c[i],c)
                if submincoins==-1:continue #剪枝2(不纳入计算)
                mincoins=min(mincoins,submincoins+1)#"各路选最优"
           
            #"左-右-根"
            memo[target]= -1 if mincoins==float('inf') else mincoins
            return memo[target]
        return dfs(amount,coins)

#方案三：DP
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        if amount<0:return -1
        if amount==0:return 0
        #
        dp=[float('inf')]*(amount+1)
        #
        dp[0]=0
        #
        for target in range(1,amount+1):
            for coin in coins:
                if target>=coin :#and dp[target-coin]!= float('inf'):
                    dp[target]=min(dp[target],dp[target-coin]+1)
        #
        return dp[amount] if dp[amount]!=float('inf') else -1

总结

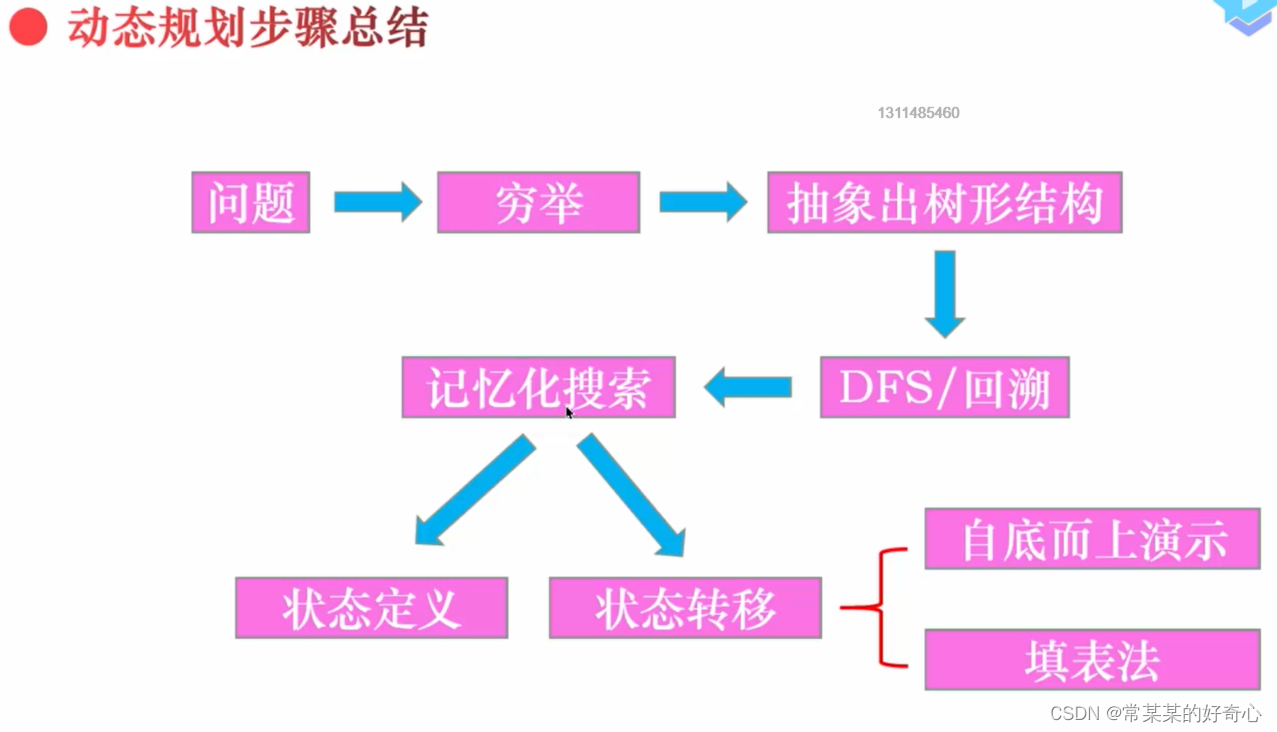
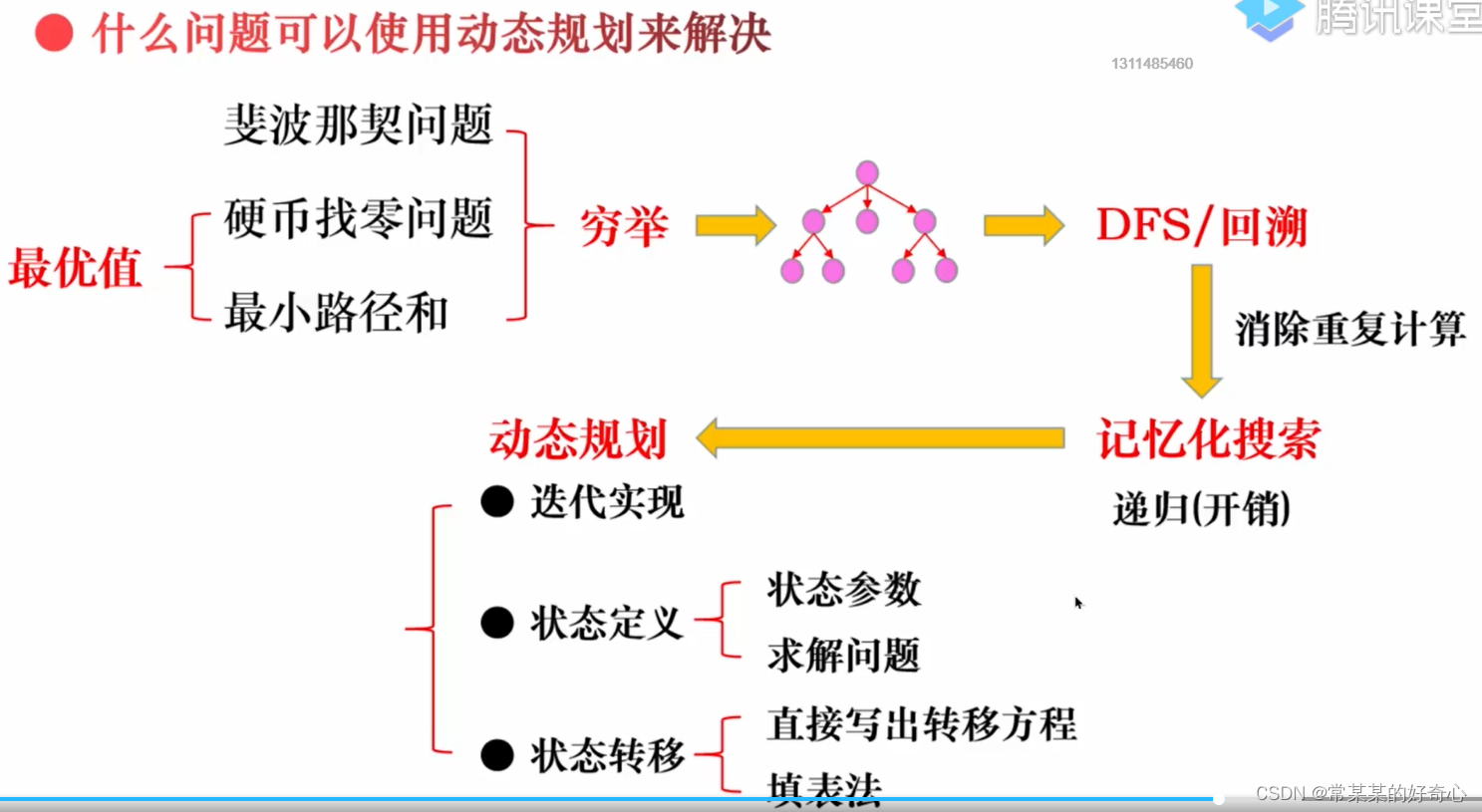
在这里插入图片描述

注意：状态参数<->节点，dp[i]状态值<->求解问题

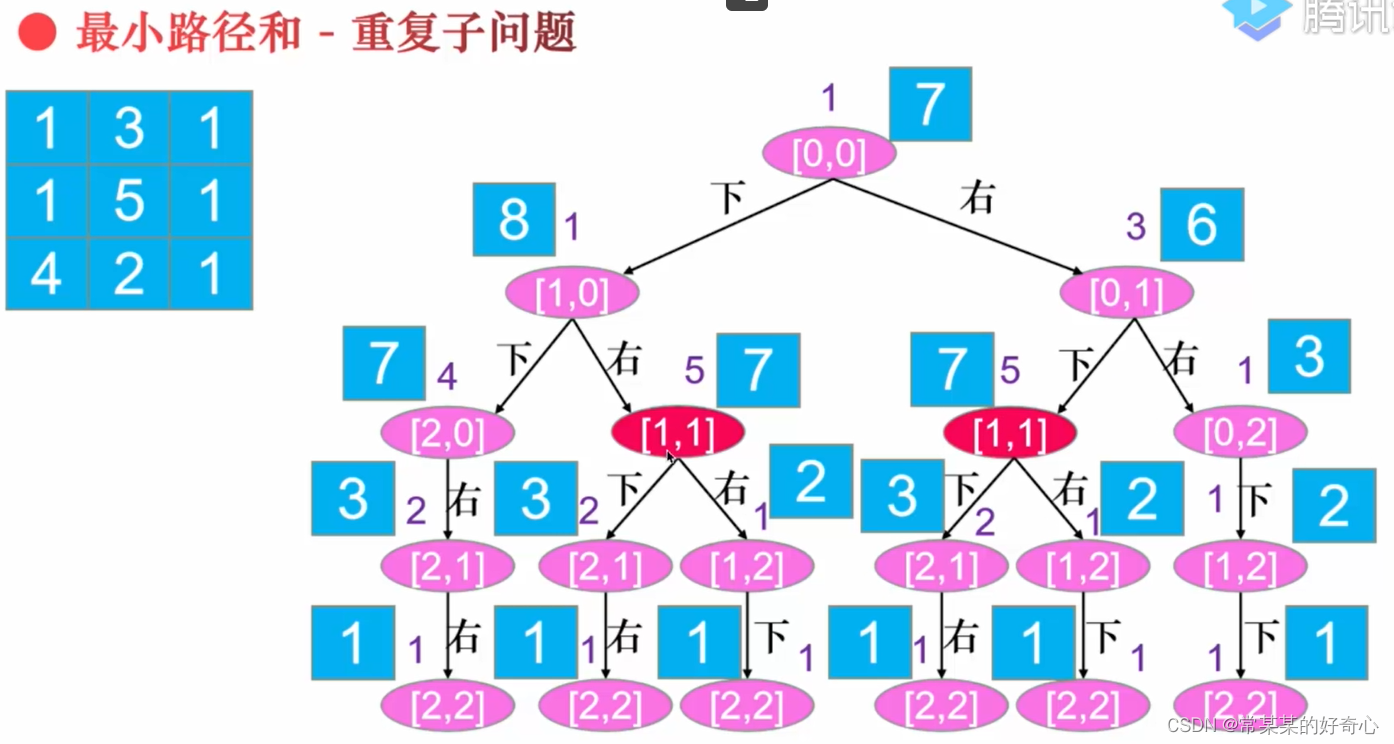
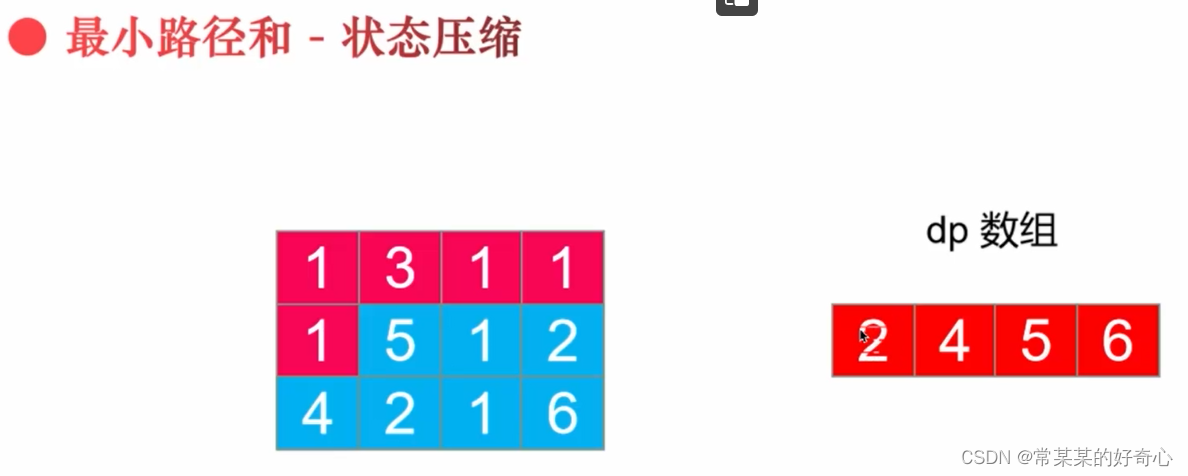
lc 64【剑指 099】【top100】：最小路径和
https://leetcode.cn/problems/minimum-path-sum/
提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100

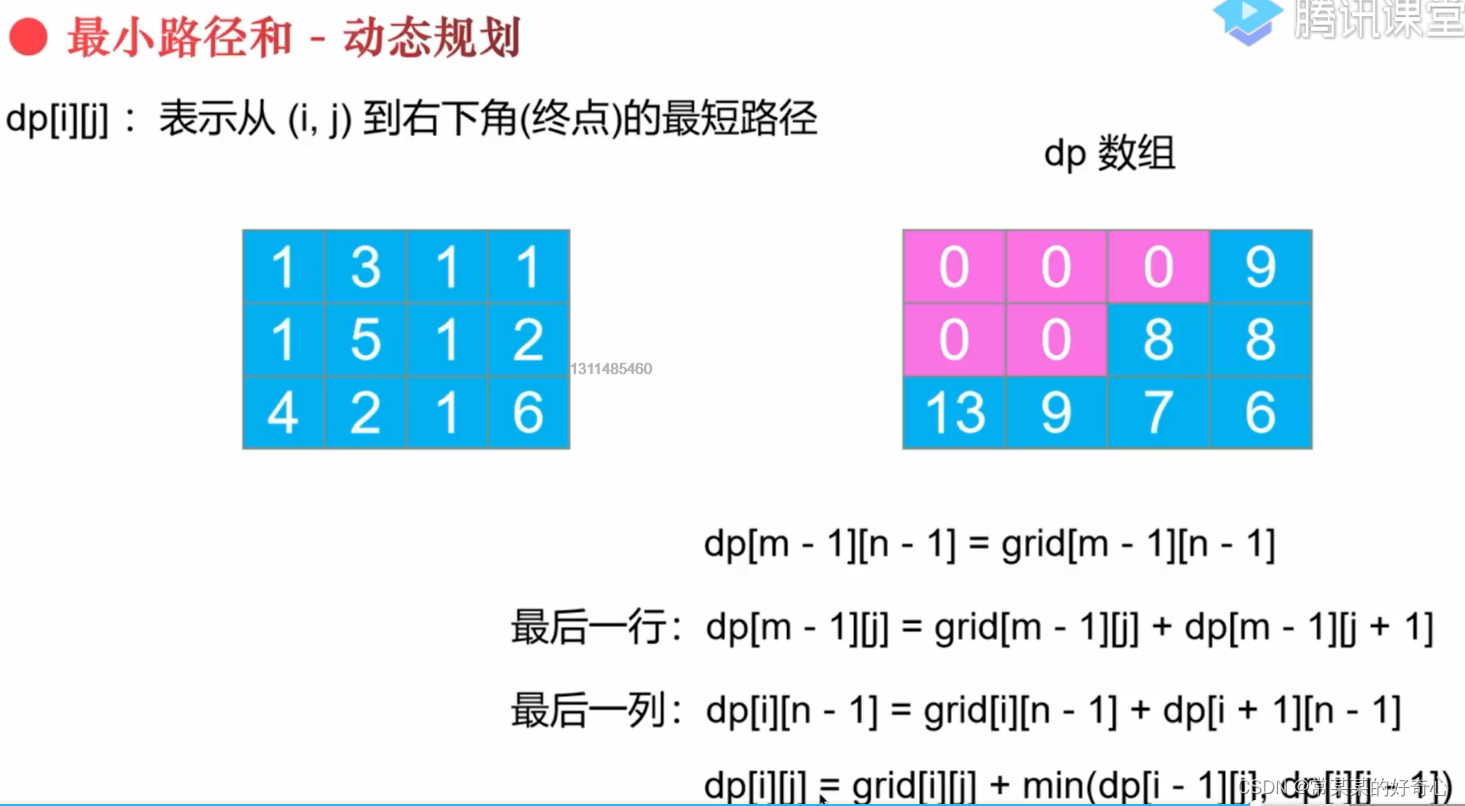
注意：dp[i][j]=dp[i][j]+min(dp[i+1][j],dp[i][j+1]

注意：state[i][j]只和上一行i-1有关

#回溯+记忆化：
class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        dirs = [[1, 0], [0, 1]]
        memo = [[float('inf')] * len(grid[0]) for _ in range(len(grid))]
        def dfs(grid,row, col):
            if row==len(grid)-1 and col==len(grid[0])-1:return grid[row][col]
            if memo[row][col] != float('inf'):return memo[row][col]
            #
            minsum = float('inf')
            for d in dirs:
                next_row, next_col = row + d[0], col + d[1]
                if next_row<0 or next_row>=len(grid) or next_col<0 or next_col>=len(grid[0]):continue
                subminsum=dfs(grid,next_row, next_col)
                minsum=min(minsum, subminsum+grid[row][col])

            memo[row][col]=minsum 
            return memo[row][col]

        return dfs(grid,0, 0)


#dp：终至起
class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m,n=len(grid),len(grid[0])
        dp=[[0]*n for _ in range(m)]
        dp[m-1][n-1]=grid[m-1][n-1]
        for i in range(m-1,-1,-1):
            for j in range(n-1,-1,-1):
                if i==m-1 and j<n-1:
                    dp[i][j]=grid[i][j] +dp[i][j+1] #key:grid[i][j]
                elif j==n-1 and i<m-1:
                    dp[i][j]=grid[i][j] +dp[i+1][j]
                elif i<m-1 and j<n-1:
                    dp[i][j]=grid[i][j] +min(dp[i + 1][j], dp[i][j + 1])
        return dp[0][0]
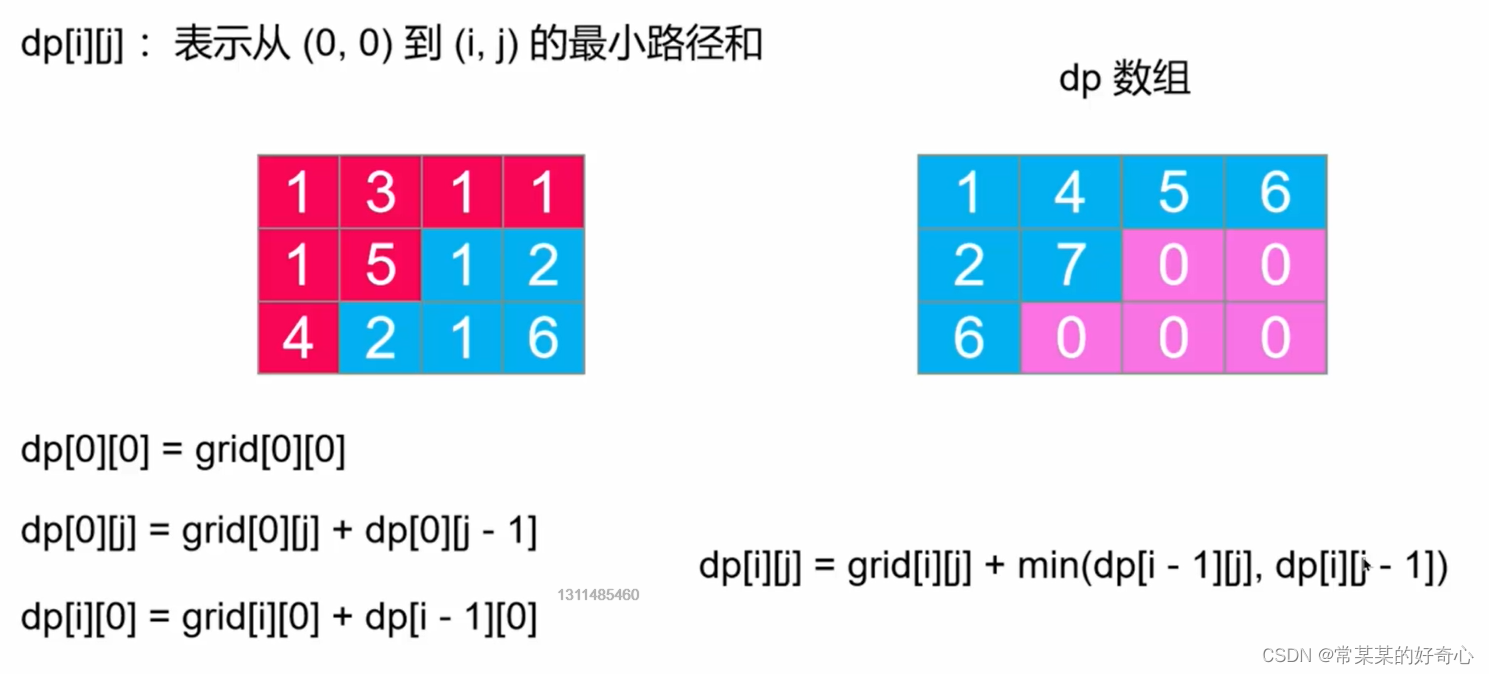
#dp：起至终
#dp：起至终+压缩
class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m,n=len(grid),len(grid[0])
        dp=[0]*n
        dp[0]=grid[0][0]
        for i in range(m):
            for j in range(n):
                if i==0 and j>0:
                    dp[j]=grid[i][j]+dp[j-1] #key:grid[i][j]
                elif j==0 and i>0:
                    dp[j]=grid[i][j] +dp[j]
                elif i>0 and j>0:
                    dp[j]=grid[i][j] +min(dp[j], dp[j-1])
        return dp[n-1]
#dp：起至终+数组本身作为状态数组
class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        for i in range(m):
            for j in range(n):
                if i == 0 and j!= 0:
                    grid[i][j] = grid[i][j] + grid[i][j - 1]
                elif i!=0 and j ==0:
                    grid[i][j] = grid[i][j] + grid[i - 1][j]
                elif i != 0 and j != 0:
                    grid[i][j]=grid[i][j]+min(grid[i-1][j],grid[i][j-1])

        return grid[m - 1][n - 1]

lc 53【剑指 42】【top100】：最大子数组之和
https://leetcode.cn/problems/maximum-subarray/
提示：
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
进阶：
如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

在这里插入图片描述

#方案一：dp(”前缀和解法“)(超时)
#方案二：dp(改变状态定义)
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        dp=[0]*len(nums)
        maxsum=dp[0]=nums[0]
        for i in range(1,len(nums)):
            dp[i]=max(dp[i-1]+nums[i],nums[i])#key更新:当前[0,i]内的所有子数组中的最大和，与上一状态的关系
            maxsum=max(maxsum,dp[i])
        return maxsum
        
#方案三：dp(改变状态定义)+压缩（只依赖前一个状态)
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        maxsum=prevmaxsum=nums[0]
        for i in range(1,len(nums)):
            prevmaxsum=max(prevmaxsum+nums[i],nums[i])#key更新:当前[0,i]内的所有子数组中的最大和，与上一状态的关系
            maxsum=max(maxsum,prevmaxsum)
        return maxsum

lc 647、5、131【剑指 086 、020】【top100】：回文子串
https://leetcode.cn/problems/palindromic-substrings/
https://leetcode.cn/problems/longest-palindromic-substring/
https://leetcode.cn/problems/palindrome-partitioning/
提示：
s 由小写英文字母组成

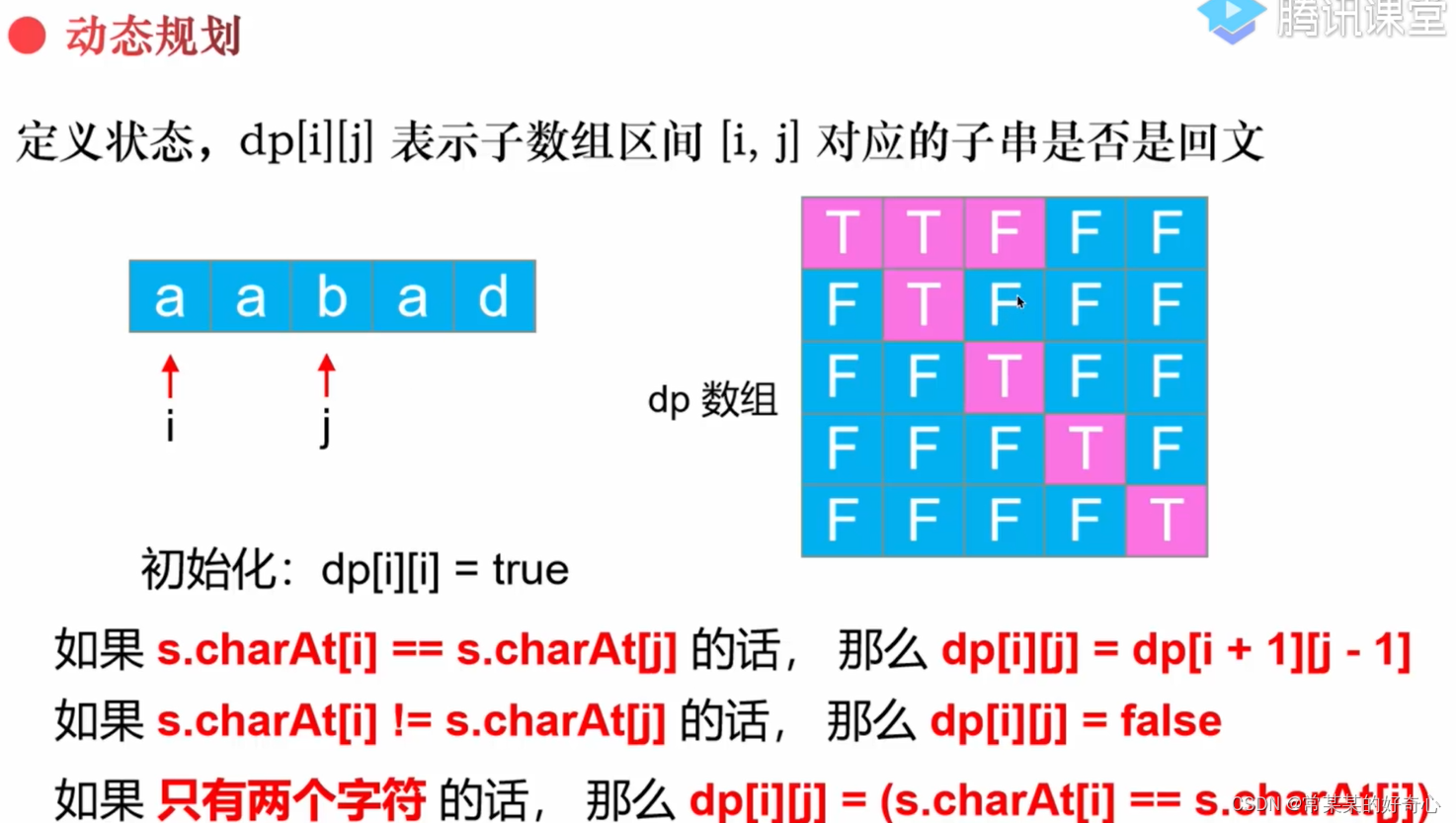
#lc 647
#dp：o（n^2）,o(n)
#注意：按列计算，下一列状态[i,j+1]依赖于前一列状态[i,j]
class Solution:
    def countSubstrings(self, s: str) -> int:
        dp=[[False]*len(s) for _ in range(len(s))]
        res=0
        #
        for i in range(len(s)):
            dp[i][i],res=True,res+1#单字符
        #按列
        for j in range(1,len(s)):
            for i in range(j):
                if j-i==1:dp[i][j]=(s[i]==s[j])#两个字符
                else:dp[i][j]=(s[i]==s[j]) and dp[i+1][j-1]
                if dp[i][j]:res+=1
        return res
#lc 5
#方案一:回溯
class Solution:
    def partition(self, s: str) -> List[List[str]]:
        def is_palindrome(str,left,right):
            while left<right:
               if str[left]!=str[right]:return False
               left,right=left+1,right-1
            return True
        #
        res=[]
        def dfs(start,path):
            if start==len(s):
                res.append(path[:])
                return
            #
            for i in range(start,len(s)):
                if not is_palindrome(s,start,i):continue #时间：O(n)
                path.append(s[start:i+1])
                dfs(i+1,path) #key:i+1
                path.pop() #易漏
        dfs(0,[])
        return res 
#方案二：回溯+dp->优化时间
class Solution:
    def partition(self, s: str) -> List[List[str]]:
        #dp存储是否回文
        dp=[[False]*len(s) for _ in range(len(s))]
        
        for i in range(len(s)):
            dp[i][i]=True
        
        for j in range(1,len(s)):
            for i in range(j):
                if j-i==1:dp[i][j]=(s[i]==s[j])
                else: dp[i][j]=(s[i]==s[j]) and dp[i+1][j-1]
        #
        res=[]
        def dfs(start,path):
            if start==len(s):
                res.append(path[:])
                return
            #
            for i in range(start,len(s)):
                if not dp[start][i]:continue #时间o(1)
                path.append(s[start:i+1])
                dfs(i+1,path) #key:i+1
                path.pop() #易漏
        dfs(0,[])
        return res 
#lc 131
class Solution:
    def longestPalindrome(self, s: str) -> str:
        dp=[[False]*len(s) for _ in range(len(s))] 
        #
        for i in range(len(s)):
            dp[i][i]=True#单字符
        #按列
        res=s[0]
        for j in range(1,len(s)):
            for i in range(j):
                if j-i==1:dp[i][j]=(s[i]==s[j])#两个字符
                else:dp[i][j]=(s[i]==s[j]) and dp[i+1][j-1]
                if dp[i][j] and j-i+1>len(res):
                    res=s[i:j+1]
        #
        return res

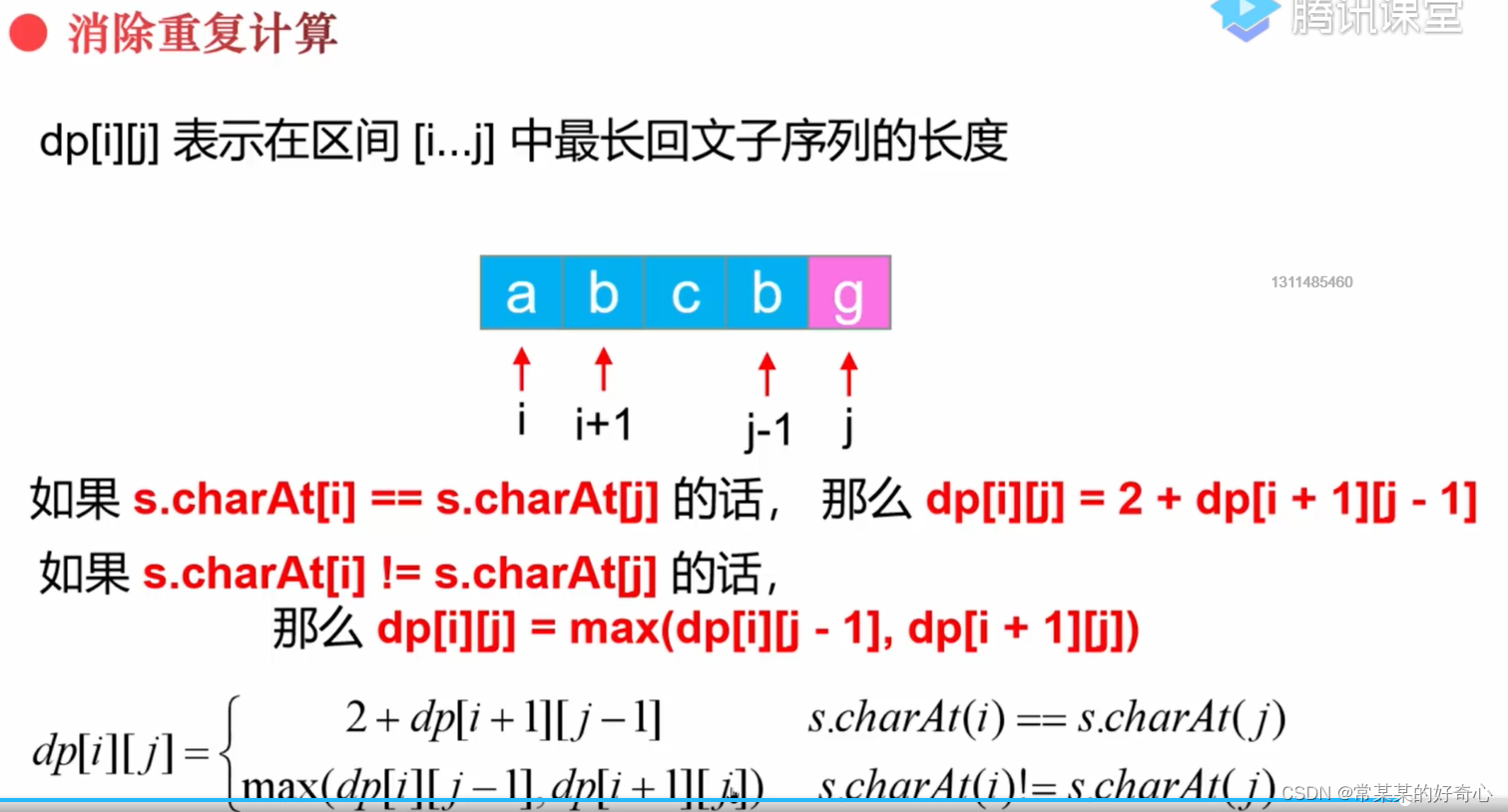
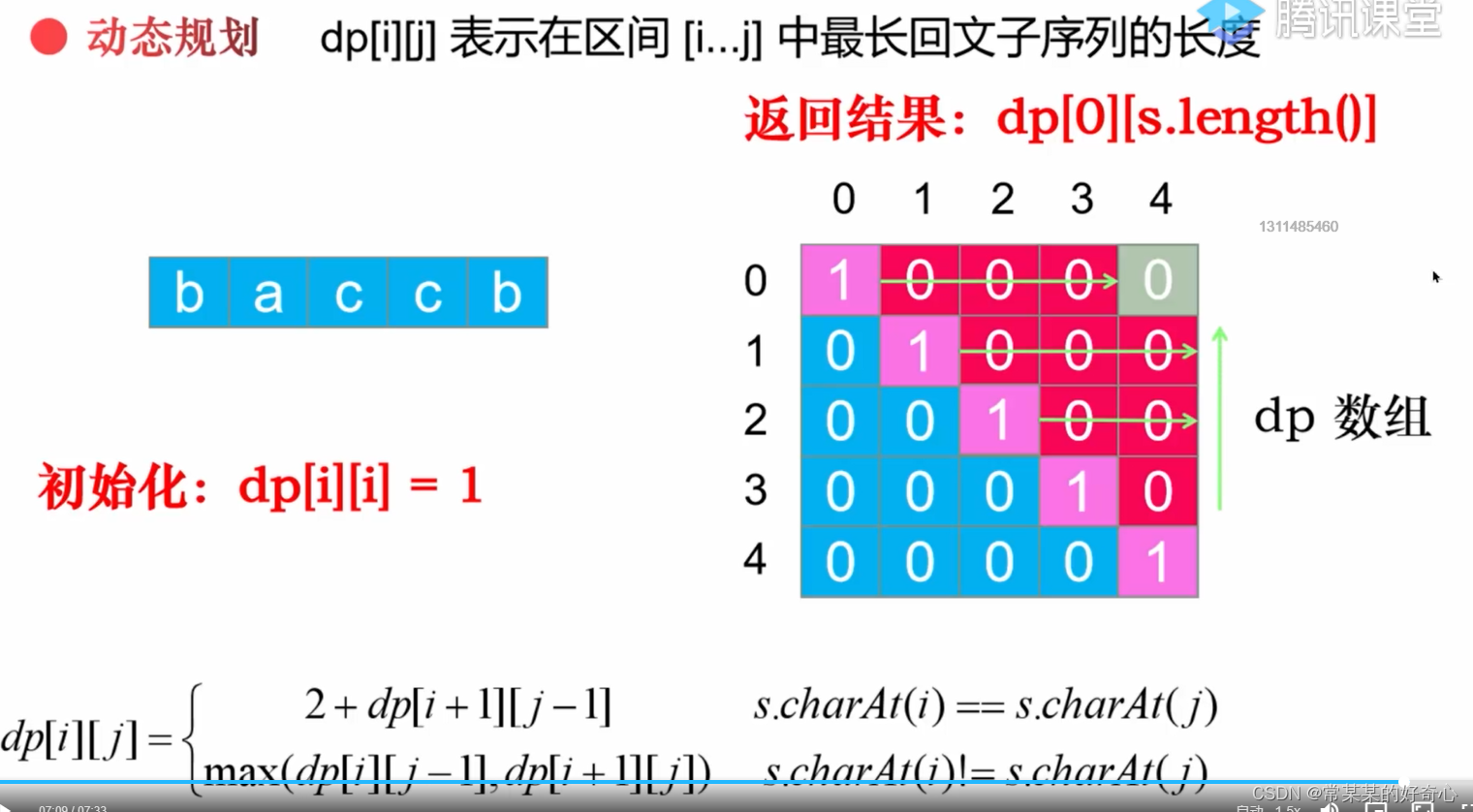
lc 516 ：最长回文子序列
https://leetcode.cn/problems/longest-palindromic-subsequence/
提示：
1 <= s.length <= 1000
s 仅由小写英文字母组成

#子数组连续，但子序列可以不连续
class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        m=len(s)
        dp=[[0]*m for _ in range(m)]
        
        for i in range(m):
            dp[i][i]=1
        
        for i in range((m-1)-1,-1,-1):
            for j in range(i+1,m):
                if s[i]==s[j]:dp[i][j]=dp[i+1][j-1]+2
                else:dp[i][j]=max(dp[i][j-1],dp[i+1][j])
        
        return dp[0][m-1]

lc 300【top100】：最长上升子序列
https://leetcode.cn/problems/longest-increasing-subsequence/
提示：
1 <= nums.length <= 2500
-104 <= nums[i] <= 104
进阶：
你能将算法的时间复杂度降低到 O(n log(n)) 吗?

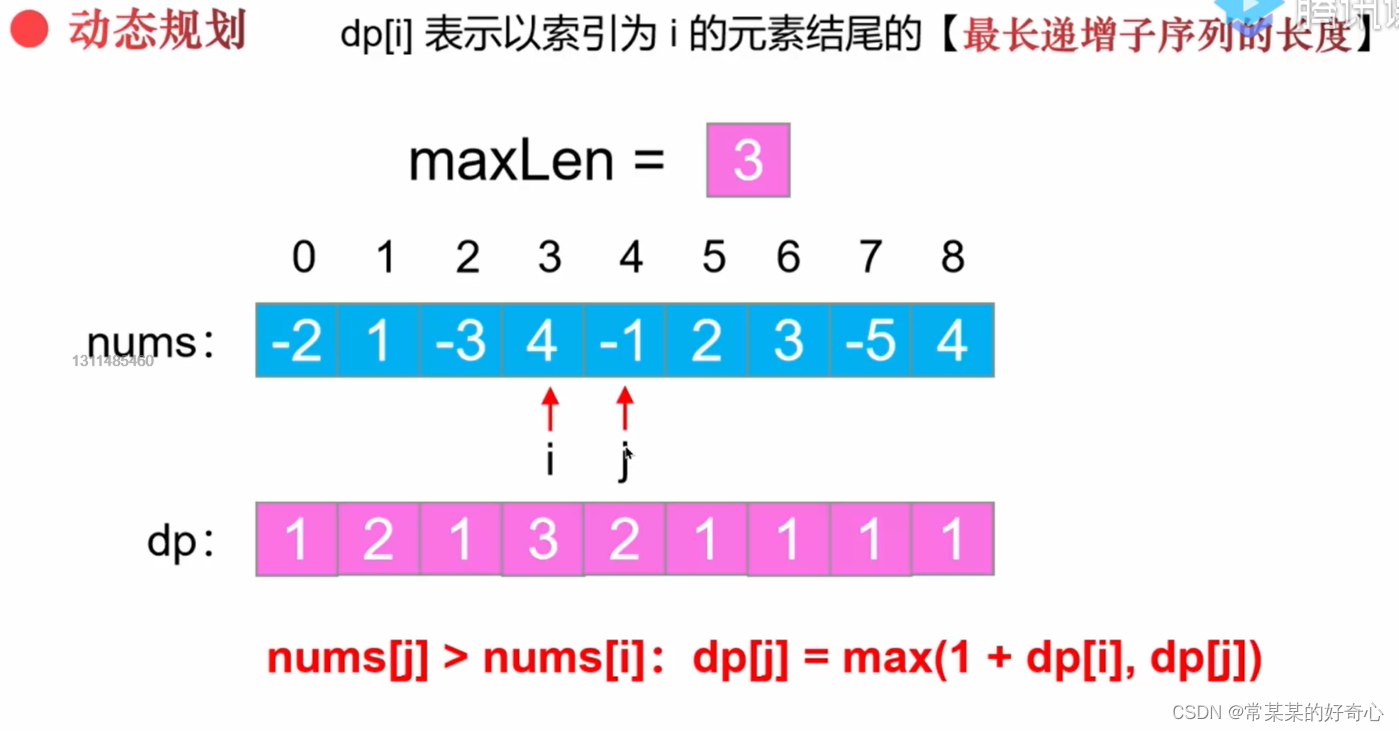
在这里插入图片描述

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        dp=[1]*(len(nums))
        
        maxl=1
        for j in range(1,len(nums)):
            for i in range(j):
                if nums[j]>nums[i]:
                    dp[j]=max(dp[i]+1,dp[j])
                    maxl=max(maxl,dp[j])
        
        return maxl

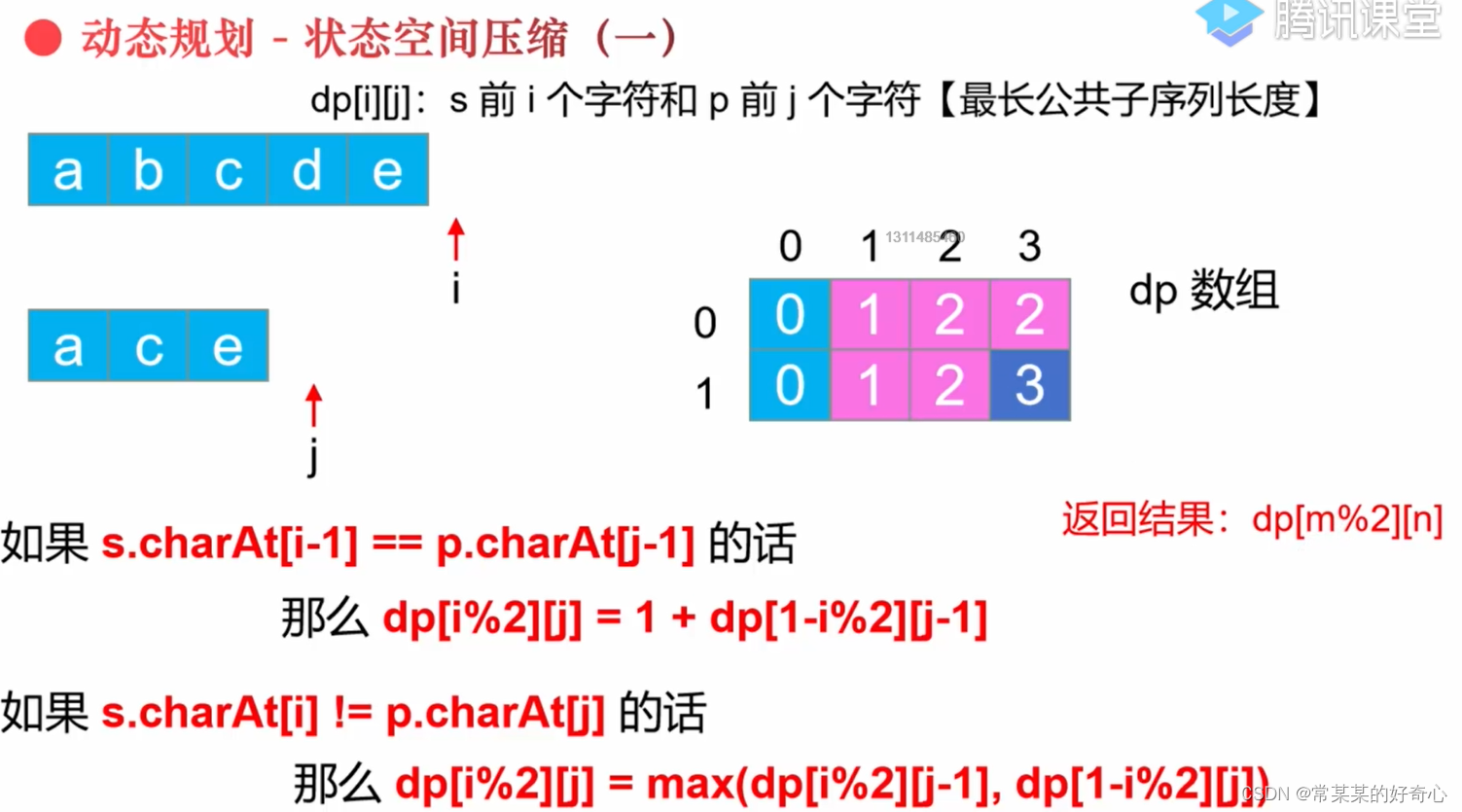
lc 1143【剑指 095】：最长公共子序列
https://leetcode.cn/problems/longest-common-subsequence/
提示：
1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成。

#方案一：dp
class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m,n=len(text1),len(text2)
        dp=[[0]*(n+1) for _ in range(m+1)]
        
        for i in range(1,m+1):
            for j in range(1,n+1):
                if text1[i-1]==text2[j-1]:
                    dp[i][j]=dp[i-1][j-1]+1
                else:
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1])
        
        return dp[m][n]
#dp+压缩
class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m,n=len(text1),len(text2)  
        dp=[[0]*(n+1) for _ in range(2)]

        for i in range(1,m+1):
            for j in range(1,n+1):
                if text1[i-1]==text2[j-1]:
                    dp[i%2][j]=dp[1-i%2][j-1]+1
                else:
                    dp[i%2][j]=max(dp[1-i%2][j],dp[i%2][j-1])
        
        return dp[m%2][n]
#dp+压缩优化
class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m,n=len(text1),len(text2)  
        #
        dp=[0]*(n+1)
        #key:prerow,prerowprecol,dp[j-1]
        prerow=0
        for i in range(1,m+1):
            #key-prerow:例如abcde<->a，1)要么有相等的，直接prerowprecol+1=1，而prerowprecol初始一定为0;2)bbcde<->a,要么无相等的，prerow=prerowprecol=0->0
            prerow=prerowprecol=0 
            for j in range(1,n+1):
                #更新(位置改变)
                prerowprecol=prerow
                prerow=dp[j]                
                #
                if text1[i-1]==text2[j-1]:
                    dp[j]=prerowprecol+1
                else:
                    dp[j]=max(prerow,dp[j-1])
               
        return dp[n]

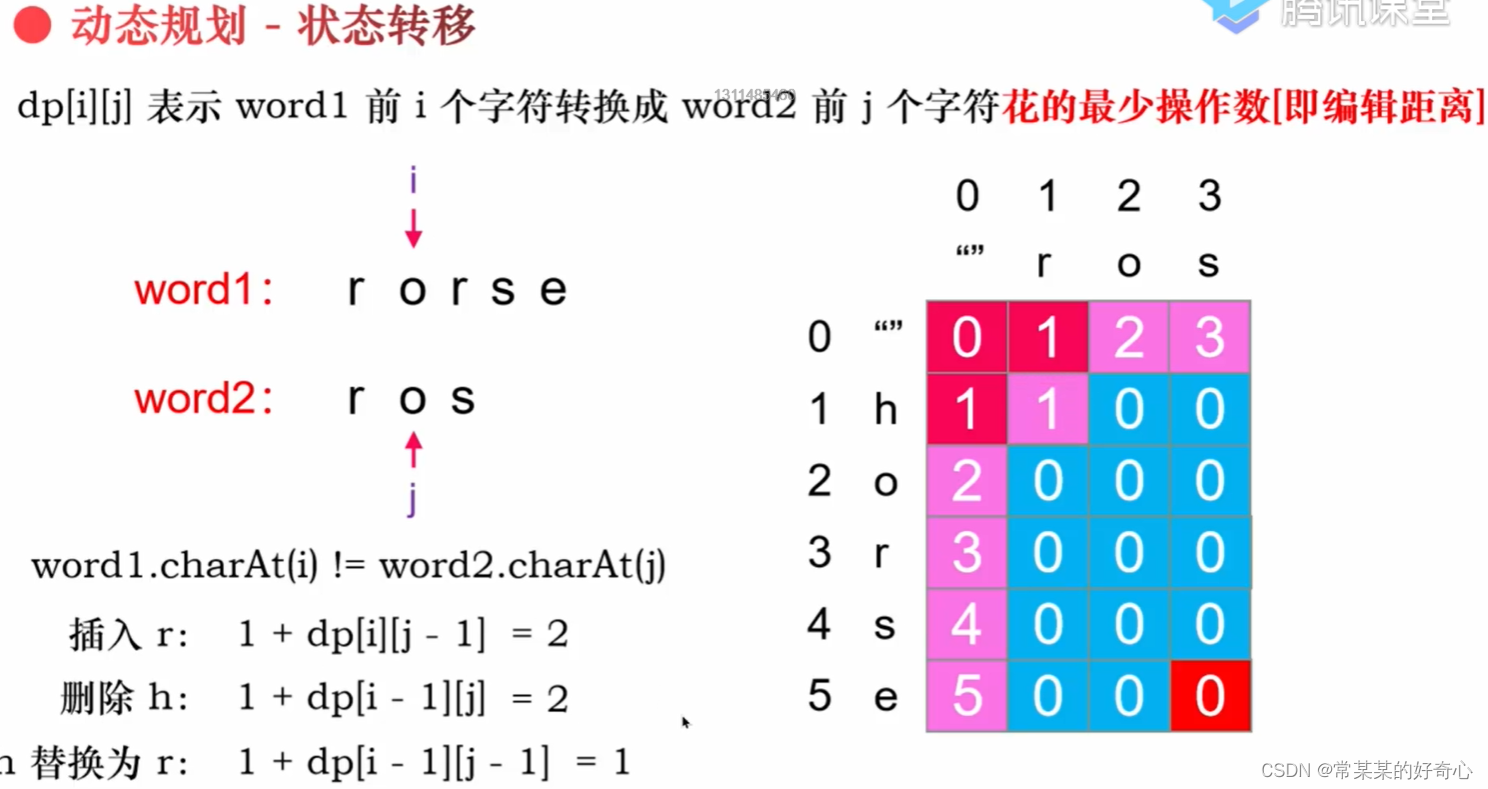
lc 72【top100】：编辑距离
https://leetcode.cn/problems/edit-distance/
提示：
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成

注意：word1.charAt(i-1) != word2.charAt(j-1)

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        m,n=len(word1),len(word2)
        
        dp=[[0]*(n+1) for _ in range(m+1)]
        
        for i in range(m+1):
            dp[i][0]=i
        for j in range(n+1):
            dp[0][j]=j
        
        for i in range(1,m+1):
            for j in range(1,n+1):
                if word1[i-1]==word2[j-1]:
                    dp[i][j]=dp[i-1][j-1]
                else:
                    insert=1+dp[i][j-1]
                    delete=1+dp[i-1][j]
                    change=1+dp[i-1][j-1]#1:本身操作算1+与之前状态关系
                    dp[i][j]=min(insert,min(delete,change))
        return dp[m][n]

lc 44 ：通配符匹配
https://leetcode.cn/problems/wildcard-matching/
说明:
s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 *。

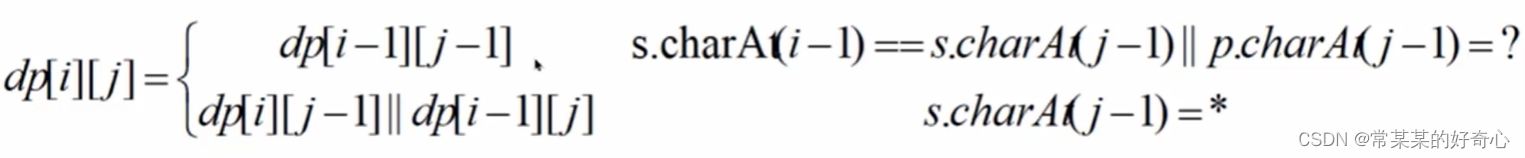
在这里插入图片描述

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        m,n=len(s),len(p)
        dp=[[False]*(n+1) for _ in range(m+1)]
        
        dp[0][0]=True
        # for i in range(1,m+1):
        #     dp[i][0]=False
        for j in range(1,n+1):
            #空字符与'*'的匹配
            if dp[0][j-1] and p[j-1]=='*':#dp的j-1指前j-1个字符，而p的j-1指第j个字符
                dp[0][j]=True
        
        for i in range(1,m+1):
            for j in range(1,n+1):
                if s[i-1]==p[j-1] or p[j-1]=='?':
                    dp[i][j]=dp[i-1][j-1]
                elif p[j-1]=='*':
                    #难点:1）'a'b<->a'*':'*'匹配‘’ 2)ac‘b’c<->a‘*’d:'*'匹配b，如[i-1][j]匹配，则[i][j]也匹配(因为'*'可以匹配字符串)
                    dp[i][j]=dp[i][j-1] or dp[i-1][j] 
        
        return dp[m][n]

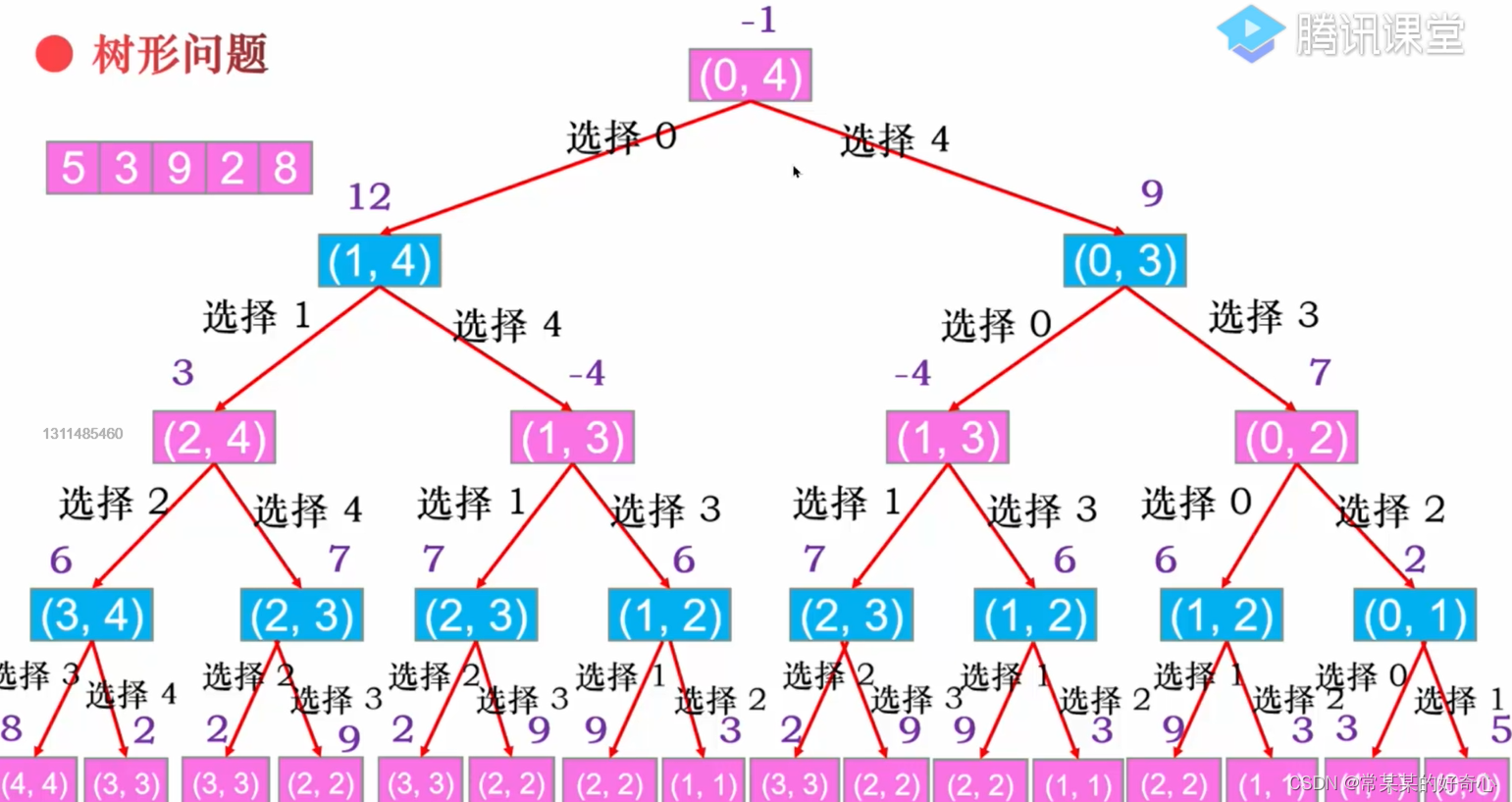
lc 486 ：预测赢家
https://leetcode.cn/problems/predict-the-winner/
提示：
1 <= nums.length <= 20
0 <= nums[i] <= 10^7

#方案一：回溯+记忆化搜索
class Solution:
    def PredictTheWinner(self, nums: List[int]) -> bool:
        memo=[[float('-inf')]*len(nums) for _ in range(len(nums))]
        
        def dfs(i,j):
            if i==j:return nums[i]
            if memo[i][j]!=float('-inf'):return memo[i][j] #在剩下[i,j]区间，玩家1比玩家2所能赢得的最高分数差
            #
   			#key-key:1)玩家1拿nums[i](/j)，玩家2所能获得的最大赢差dp[i+1][j](/dp[i][j-1])
            #2）或者玩家2拿nums[j](/i)，玩家1所能获得的最大赢差dp[i+1][j](/dp[i][j-1])
            #3)但是，起始总是从玩家1开始
            pick_i=nums[i]-dfs(i+1,j) #玩家1先选-玩家2后选
            pich_j=nums[j]-dfs(i,j-1)
            memo[i][j]=max(pick_i,pich_j)
            return memo[i][j]

        return dfs(0,len(nums)-1)>=0
#方案二：dp
class Solution:
    def PredictTheWinner(self, nums: List[int]) -> bool:
        m=len(nums)
        dp=[[float('-inf')]*len(nums) for _ in range(len(nums))]#在剩下[i,j]区间，玩家1(/2)比玩家2(/1)所能赢得的最高分数差

        for i in range(m):
            dp[i][i]=nums[i]

        #key-key-key:转移方向
        for i in range(m-2,-1,-1):
            for j in range(i+1,m):
                    dp[i][j]=max(nums[i]-dp[i+1][j],nums[j]-dp[i][j-1])

        return dp[0][m-1]>=0 #注意索引位置