树
树是一种特殊的图 。
特点:
- 若树有n个点,则有n-1条边。
- 树有连通性但没有回路。
- 从一个点出发可以到达任意一个,而且路径是唯一的。
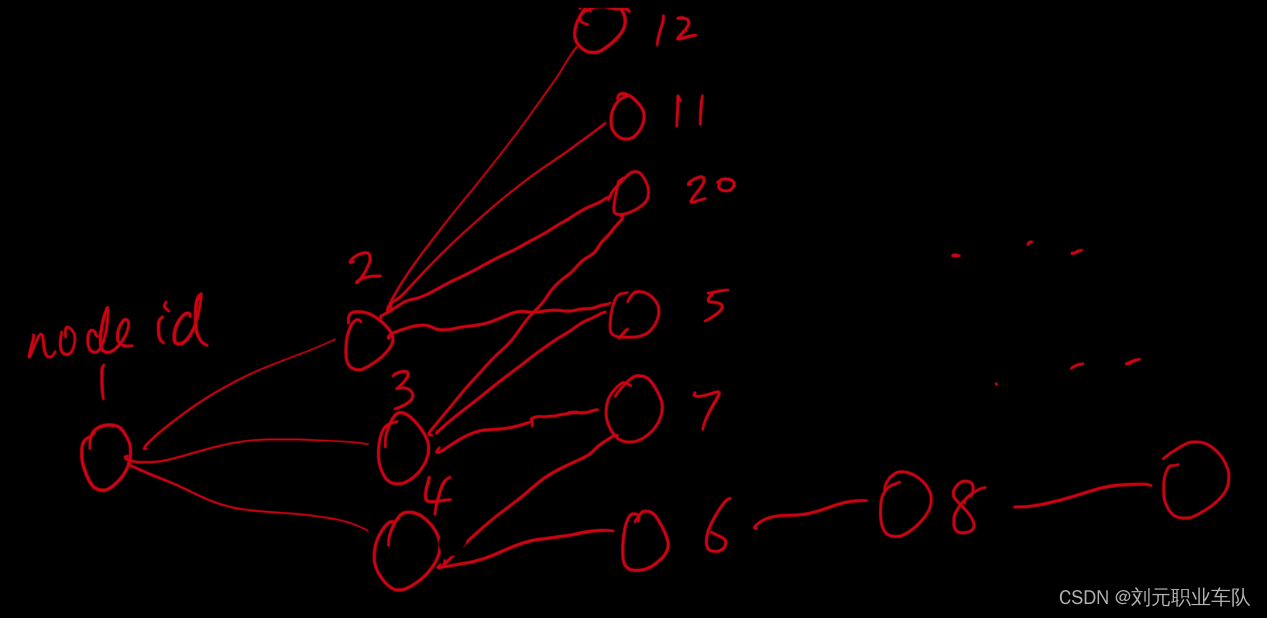
树的重心u(最平衡的点):
- 以树上任意一个结点为根计算它的子树的结点数,如果结点u的最大的子树的结点数最少,那么u就是树的重心。
- 删除点u后得到两棵或更多棵互不连通的子树,其中最大子树的结点数最小。u是树上最平衡的点。
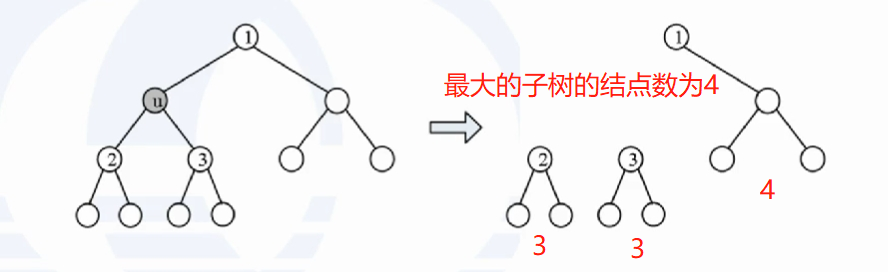 若删除① ,得到两棵子树,节点数分别为7和3,最大的子树的结点数为7,比4大,不是重心。
若删除① ,得到两棵子树,节点数分别为7和3,最大的子树的结点数为7,比4大,不是重心。
如何计算以结点i为根的子树的结点数量?
- 对i做DFS:从i出发,递归到最底层后返回,每返回一个结点,结点数加1(因为每个结点只返回1次),直到所有结点都返回,就得到了子树上结点总数。

如何寻找重心u?
暴力法(O()):
- 删除树上的一个结点u,得到几个孤立的连通块,可以对每个连通块做一次DFS,分别计算结点数量。
- 对整棵树逐一删除每个结点,重复上述计算过程,就得到了每个结点的最大连通块。
优化(O(n)):只需要一次DFS,就能得到每个结点的最大连通块
1、删除u得到三个连通块: (1)包含1的连通块; (2) 包含2 的连通块, (3) 包含3的连通块。
 2、这三个连通块的数量如何计算?
2、这三个连通块的数量如何计算?
从任意一个点开始DFS,假设从1开始,1是u的父结点。DFS到结点u后,从u开始继续DFS,得到它的子树2和3的结点数量(2) 和(3),设u为根的子树的结点数量是d[u],则d[u]=(2)+(3)+1。那么 (1)的数量等于n-d[u],n是结点总数。记录(1)、 (2)、 (3)的最大值,就得到了u的最大连通块。
这样通过一次DFS,每个结点的最大连通块都得到了计算,总复杂度O(n)。
例题
【问题描述】城里有一个黑手党组织。把黑手党的人员关系用一棵树来描述,教父是树的根,每个结点是一个黑手党徒。为了保密,每人只和他的父结点和他的子结点联系。警察知道哪些人互相来往,但是不知他们的关系。警察想找出谁是教父。
警察假设教父是一个聪明人:教父懂得制衡手下的权力,所以他直属的几个小头目,每个小头目属下的人数差不多。也就是说,删除根之后,剩下的几个互不连通的子树(连通块),其中最大的连通块应该尽可能小。帮助警察找到哪些人可能是教父。
【输入】第一行是n,表示黑手党的人数,2≤n ≤50000。黑手党徒的编号是1到n。下面有n-1行,每行有2个整数,即有联系的2个人的编号。
【输出】输出疑似教父的结点编号,从小到大输出。
复杂度分析:n最大是50000,最大复杂度可以O(nlogn),DFS复杂度为O(n),没有问题。
import sys
sys.setrecursionlimit(300000)
def dfs(u,fa):
global num,maxnum # num:教父的数量;
d[u] = 1 # 递归到最底层时,结点数加1
tmp = 0
# 处理u的所有子树:计算把u中所有子树的结点数量,保存在d[u],记录u中最大子树的结点数量
for v in edges[u]: # 遍历u的子结点
if v == fa: continue # 不递归父亲,因为可以用n - d[u]直接算出来
dfs(v,u) # 递归子结点,计算v这个子树的结点数量
d[u] += d[v] # 计算以u为根的结点数量
tmp = max (tmp,d[v]) # 记录u的最大子树的结点数量
tmp = max (tmp,n - d[u]) # tmp = u的最大连通块的结点数。(n - d[u]:父结点所在的子树的结点数)
# 以上计算出了u的最大连通块
# 下面统计疑似教父。如果一个结点的最大连通块比其他结点的都小,它是疑似教父
if tmp < maxnum: # 如果发现一个疑似教父比之前的教父的最大连通块要小
maxnum = tmp # 更新“最小的”最大连通块
num = 1 # 之前的都不要了,num=1重新统计
ans[1] = u # 把教父记录在第1个位置(不用ans[0])
elif tmp == maxnum: # 和“最小的”最大连通块结点数相等,也是疑似教父
num += 1
ans[num] = u # 疑似教父有多个,记录在后面
maxnum = int (1e9) # 无穷大,用来作比较最大子树的结点
n = int (input())
d = [0]*(n+1) # d[u]:以u为根的子树的结点数量
ans = [0]*(n+1) # 记录教父
num = 0 # 教父的数量
edges = [[] for i in range(n+1)]
for i in range(n-1):
a, b = map(int,input().split())
edges[a].append(b) # a行加入邻居点(与a相连的点)
edges[b].append(a) # b行加入邻居点
dfs(1,0) # 做一次DFS求出所有教父。从任意一点开始都可以,如果不清楚树结点之间的关系,默认选择1开始,父亲为0(不存在).
s = sorted(ans[1 :num+1]) # 对教父排序。sorted返回一个列表
for i in range(num): print(s[i], end=' ') # 按顺序打印所有教文树的直径
树的直径是指树上最远的两点间的距离,又称为树的最远点对。
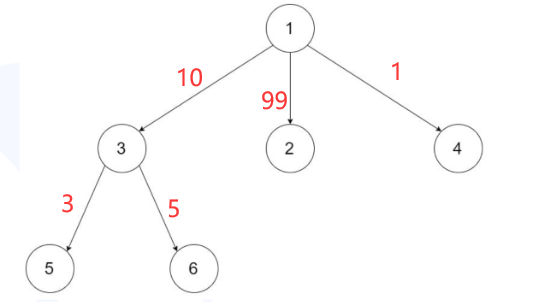
从上图可知,最远的两点为2和6,距离为114。
有两种方法求树的直径:
- 做两次DFS (或BFS)
- 树形DP
复杂度都是O(n)
优点和缺点:
(1)做两次DFS(或BFS)
- 优点:能得到完整的路径。它用搜索的原理,从起点u出发一步一步求u到其他所有点的距离,能记录路径经过了哪些点。
- 缺点:不能用于有负权边的树。
(2)树形DP
- 优点:允许树上有负权边。
- 缺点:只能求直径的长度,无法得到这条直径的完整路径。
树的直径例题
【问题描述】求树的直径。
【输入描述】第一行是整数n,表示树的n个点。点的编号从1开始。后面n-1行,每行3个整数a、b、w,表示点a、b之间有一条边,边长为w。
【输出描述】一个整数,表示树的直径。
方法一:做两次DFS
当边权没有负值时,计算树的直径可以通过做两次DFS解决,步骤是:
- 从树上的任意一个点r出发,用DFS求距离它最远的点s。s肯定是直径的两个端点之一。
- 从s出发,用DFS求距离s最远的点t。t是直径的另一个端点。s、t就是距离最远的两个点,即树的直径的两个端点。
这个方法不能用于有负权边的树。例:
- 第一次DFS,若从点1出发,得到的最远端点s为点2;
- 第二次DFS从点2出发,得t为点4。
- 但是,实际上这棵树的直径的两个端点应该是3、4。
总结:以贪心原理进行路径长度搜索的DFS,当树上有负权边时,只能在局部获得最优,而无法在全局获得最优。
import sys
sys.setrecursionlimit(300000)
def dfs(u,father,d): # 用dfs计算从u到每个子结点的距离
dist[u] = d # u到该点的距离d
for v,w in edges[u]: # 遍历u的所有邻居
if v != father: # 很关键,不回头搜父结点
dfs(v,u,d+w)
n = int(input())
dist = [0]*(n+1) # 一维数组:记录距离
edges = [[] for i in range(n+1)] # 存储树:结点的关系
for i in range(n-1):
a, b,w = map(int,input().split())
edges[a].append((b,w)) # a行加入邻居点b和对应的距离w
edges[b].append((a, w))
# 从任意一点出发,默认从1出发,父亲为-1,距离为0
dfs(1,-1,0) # 求出1到其他点的距离,记录在dist。
s = 1
for i in range (1, n+1): # 找最远的结点s,s是直径的一个端点
if dist[i]>dist[s]: s = i
dfs(s,-1,0) # 从s出发,计算以s为起点,到树上每个结点的距离
t = 1
for i in range(1, n+1): # 找距离s最远的点t,t就是直径的另一个端点
if dist[i]>dist[t]: t = i
print(dist[t]) # 打印树的直径的长度(s到t的距离)拓扑排序与DFS
- 设有a、b、c、d等事情,其中a有最高优先级,b、c优先级相同,d是最低优先级,表示为a→(b, c)→ d,那么abcd或者acbd都是可行的排序。
- 把事情看成图的点,先后关系看成有向边,问题转化为在图中求一个有先后关系的排序,这就是拓扑排序。
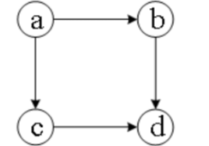
- 出度:以点u为起点的边的数量,称为u的出度。例如上图点a的出度为2
- 入度:以点v为终点的边的数量,称为v的入度。例如上图点d的入度为2
- 一个点的入度和出度,体现了这个点的先后关系。如果一个点的入度等于0,说明它是起点,是排在最前面的;如果它的出度等于0,说明它是终点。
- 图中,点a的入度为0,它们都是优先级最高的事情;d的出度为0,它的优先级最低。
用DFS解拓扑排序
- DFS天然适合拓扑排序。
- DFS深度搜索的原理,是沿着一条路径一直搜索到最底层,然后逐层回退。
- 这个过程正好体现了点和点的先后关系,天然符合拓扑排序的原理。
操作
①如果只有一个点u是0入度的
- 那么从u开始DFS,DFS递归返回的顺序就是拓扑排序(是一个逆序)。
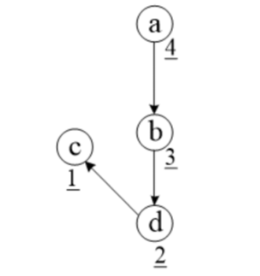
- DFS递归返回的首先是最底层的点,它一定是0出度点,没有后续点,是拓扑排序的最后一个点;然后逐步回退,最后输出的是起点u;输出的顺序是一个逆序。
- 从a开始,递归返回的顺序见点旁边的划线数字: cdba,是拓扑排序的逆序。
②如果有多个入度为0的点
- 想象有一个虚拟的点v,它单向连接到所有其他点。这个点就是图中唯一的0入度点,图中所有其他的点都是它的下一层递归;而且它不会把原图变成环路。从这个虚拟点开始DFS(可以从任意一个点出发,不需要找入度为0的点),就完成了拓扑排序。
- 图(1)有2个0入度点a和f
- 图(2)想象有个虚拟点v,递归返回的顺序见点旁边划线数字,返回的是拓扑排序的逆序。
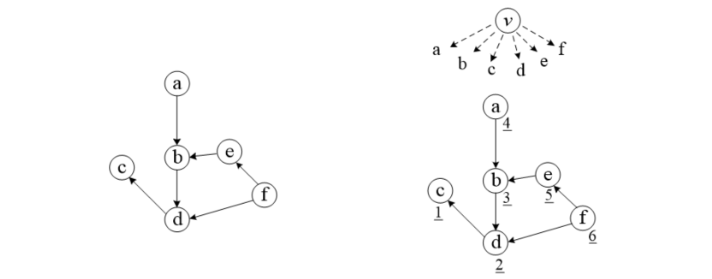 图(2)可以从任意一个点出发返回的顺序都是一样的,例如从a出发,a-b-d-c,然后从c开始返回到a,顺序为1c-2d-3b-4d。然后下次再从e出发,发现下一个点b已经访问过,结束返回5e,最后从f出发,发现下一个点e已经访问过,结束返回6f,所以递归返回的顺序是cdbaef(拓扑排序的逆序)。从b开始,b-d-c,再返回cdb,再从a开始,b访问过,返回a,再从e开始,b访问过,返回e,最后从f开始,e访问过返回f,顺序也是cdbaef。
图(2)可以从任意一个点出发返回的顺序都是一样的,例如从a出发,a-b-d-c,然后从c开始返回到a,顺序为1c-2d-3b-4d。然后下次再从e出发,发现下一个点b已经访问过,结束返回5e,最后从f出发,发现下一个点e已经访问过,结束返回6f,所以递归返回的顺序是cdbaef(拓扑排序的逆序)。从b开始,b-d-c,再返回cdb,再从a开始,b访问过,返回a,再从e开始,b访问过,返回e,最后从f开始,e访问过返回f,顺序也是cdbaef。
欧拉路与DFS
欧拉路:从图中某个点出发,遍历整个图,图中每条边通过且只通过一次。(一笔画游戏)
欧拉回路:起点和终点相同的欧拉路。
欧拉路问题:①是否存在欧拉路、②打印出欧拉路。
欧拉路的两种存在形式:①每个结点都是偶数边(欧拉回路) ②只有两个奇数边的点,一个作为起点,一个作为终点。
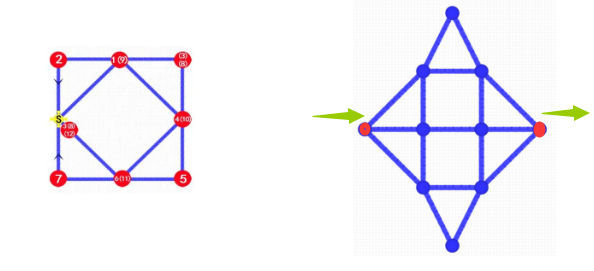
用DFS输出一个欧拉回路
对一个无向连通图做DFS,就输出了一个欧拉回路。
从图(1)中a点开始DFS,DFS的对象是边。图(2)边上的数字,是DFS访问的顺序。DFS从a点开始,a-b-d-c-a,发现a访问过了,结束返回ac。回到c后再从c开始,c-d-f-e-c,发现c访问过,结束。返回ce-ef-fd-dc,cd-db-ba。访问顺序为ab-bd-dc-ca-cd-df-fe-ec。图(3)边上的数字是回溯的顺序。顺序为ca-ce-ef-fd-dc-cd-db-ba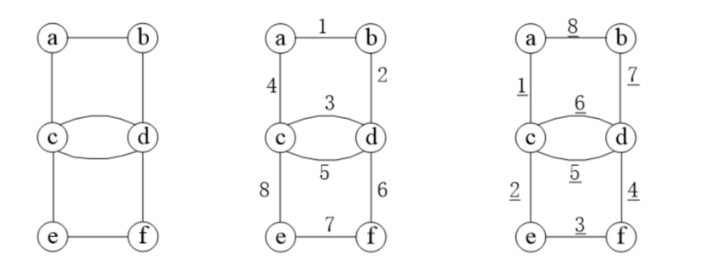


![Vivado 错误代码 [Place 30-574]解决思路](https://img-blog.csdnimg.cn/ba0aaae2d686450592b64102bcf119bd.png)