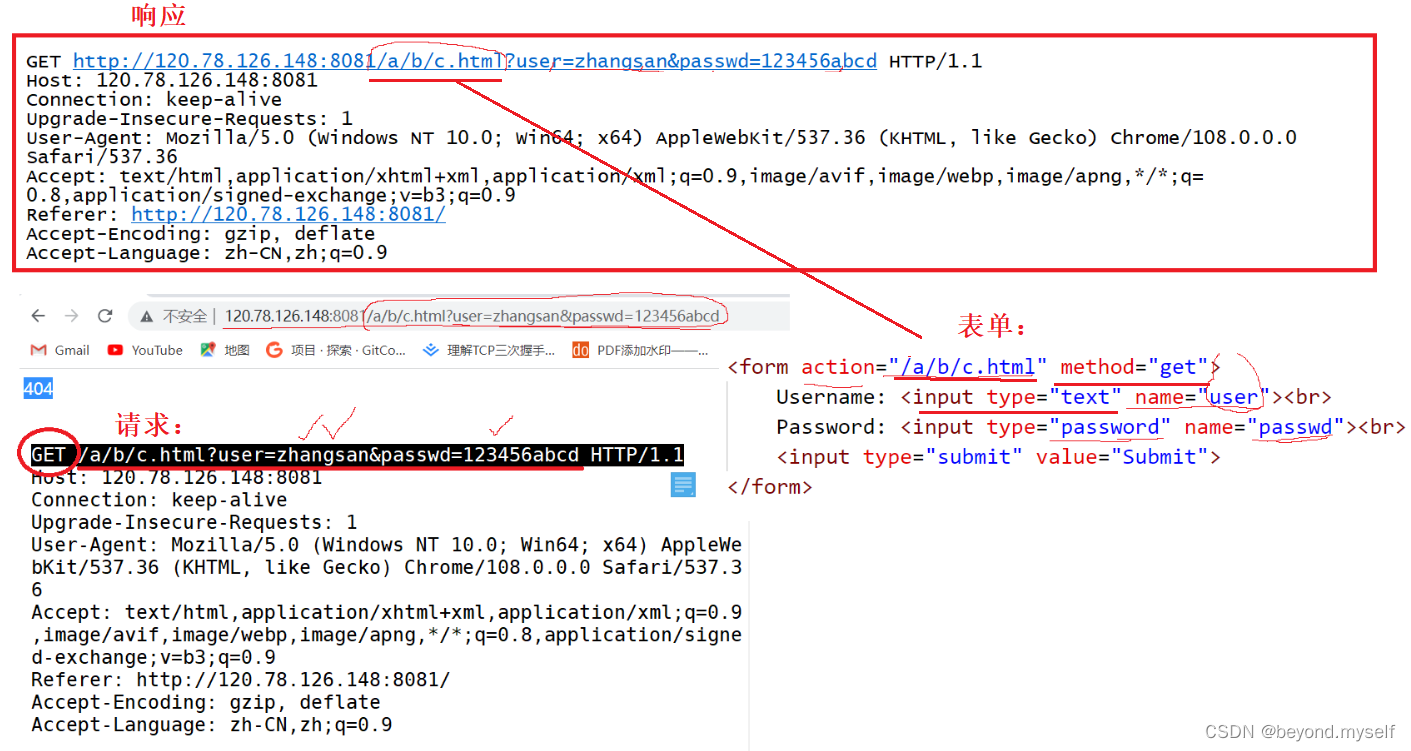
美赛B题概述:
美赛赛题类型美国大学生数学建模竞赛目前分为两种类型,MCM(Mathematical Contest In Modeling)和 ICM(Interdisciplinary Contest In Modeling),两种类型竞赛采用统一标准进行,竞赛题目出来之后,参数队伍通过美赛官网进行选题,一共分为 6 种题型。

近几年B题数据分析:



从数据可以看出,美赛每年参赛人数在逐渐增加,但是增加人数在放缓,至于2023年美赛B题选择队伍数量是不好预测的,因为美赛总体上有一个规律,容易入手的题目,选择的队伍会很多。可以分析一下获奖的情况,B题O奖的获奖率是高于全部题目的O奖获奖率的,可以总结一下,参赛队伍少的题目O奖获奖率更高的,大家在选择题目的时候可以自己把握。从这几年的B题来看,应该没有一年B题是比较简单的。不过有一个好消息,F,M的获奖比例应该差不多稳定在2%,7%.
近几年B题算法分析:
比赛前可以看看每年的O奖论文,如果没时间看的话,可以去看看他们论文的关键词的,这里就罗列一下近四年的美赛B题O奖论文关键字
2022年B题O奖论文关键字
Resource Allocation Network(RAN); Linear Programming; Marginal Utility; Auction
Theory; Marginal Utility; Independent Private Value (IPV) Model;
资源分配网络(RAN);线性规划;边际效用;拍卖理论;边际效用;独立私有价值(IPV)模型;
Transportation Model; Multi-objective Programming; Distribution and tradeoff
运输模式.多目标规划.分配和权衡
dynamic programming, multi-objective-programming, TOPSIS method
based on EWM, multi-stage discussion
动态规划、多目标规划、基于EWM的TOPSIS方法、多阶段讨论
“Double-Dam” System, Management, Difference Equation Model, Optimization Model, Multi-objective Programming, Genetic Algorithm, Principal Component Analysis
“双坝”系统、管理系统、差分方程模型、优化模型、多目标规划、遗传算法、主成分分析
Simulated Annealing, Game Theory,Newton Iteration, Water-Shortage Index
模拟退火法,博弈论,牛顿迭代法,缺水指数
2021年B题O奖论文关键字
Drone, Optimization, Regional Discretization, Fire Dynamic Models, Cellular Automata
无人机、优化、区域离散化、火灾动态模型、细胞自动机
Fighting Wildfires; Multi-Objective Optimization; Poisson Distribution; Tabu Search Algorithm; Sensitivity Analysis
扑灭野火;多目标优化;泊松分布;禁忌搜索算法;敏感性分析
safety factor, commensurable, signal-to-noise ratio
安全系数,可公度,信噪比
Drone Arrangement Model; K-means Model; Minimum Spanning Tree Model; GM Model;
无人机布置模型;K-means模型;最小生成树模型;GM模型;
Genetic Algorithm, LSTM, Multivariate Optimal Programming
遗传算法、LSTM、多变量优化规划
2020年B题O奖论文关键字
periodic sand-water cell automaton model, multivariate analysis, quantified
and visualized, concentration gradient method
周期性砂-水细胞自动机模型、多元分析、量化和可视化、浓度梯度法
Mohr-Coulomb Yielding Criteria, Horton’s equation, Van Genuchten Model, Internal friction angle, ANSYS simulation.
莫尔-库仑屈服准则,霍顿方程,范-格努钦模型,内摩擦角,ANSYS模拟。
Cellular automata, Evolutionof three-dimensional complex space-time systems, The longest lasting sandcastle foundation
细胞自动机 , 三维复杂时空系统的演变,持续时间最长的沙堡基础
3D Sandcastle Model; Fluid-Structure Interaction; Optimizing Model;
三维沙堡模型;流体-结构相互作用;优化模型;
2019年B题O奖论文关键字
Multi-Objective Programming,Dynamic Programming, Drone Rescue Model, AHP
多目标规划、动态规划、无人机救援模型、AHP
Drone, Route Planning, 3D Bin-Packing, AHP
无人机,路线规划,3D机箱包装,AHP
Drone; The location problem; The loading problem; Emergency rescue
无人机、定位问题、装载问题、紧急救援
Optimization; ACO; Gridding; Voronio; Dijkstra
优化;ACO;网格;Voronio;Dijkstra
通过对近几年的美赛B题O奖论文关键字分析,近几年的题目都可以使用优化模型的方法来解决,除此之外,细胞自动机,无人机出现频率较高。
优化模型:
数学规划模型
线性规划、整数线性规划、非线性规划、多目标规划、动态规划。
微分方程组模型
阻滞增长模型、SARS传播模型。
图论与网络优化问题
最短路径问题、网络最大流问题、最小费用最大流问题、最小生成树问题(MST)、旅行商问题(TSP)、图的着色问题。
概率模型
决策模型、随机存储模型、随机人口模型、报童问题、Markov链模型。
组合优化经典问题
l 多维背包问题(MKP)
背包问题:个物品,对物品,体积为,背包容量为。如何将尽可能多的物品装入背包。
多维背包问题:个物品,对物品,价值为,体积为,背包容量为。如何选取物品装入背包,是背包中物品的总价值最大。
多维背包问题在实际中的应用有:资源分配、货物装载和存储分配等问题。该问题属于难问题。
二维指派问题(QAP)
工作指派问题:个工作可以由个工人分别完成。工人完成工作的时间为。如何安排使总工作时间最小。
二维指派问题(常以机器布局问题为例):台机器要布置在个地方,机器与之间的物流量为,位置与之间的距离为,如何布置使费用最小。
二维指派问题在实际中的应用有:校园建筑物的布局、医院科室的安排、成组技术中加工中心的组成问题等。
旅行商问题(TSP)
旅行商问题:有个城市,城市与之间的距离为,找一条经过个城市的巡回(每个城市经过且只经过一次,最后回到出发点),使得总路程最小。
车辆路径问题(VRP)
车辆路径问题(也称车辆计划):已知个客户的位置坐标和货物需求,在可供使用车辆数量及运载能力条件的约束下,每辆车都从起点出发,完成若干客户点的运送任务后再回到起点,要求以最少的车辆数、最小的车辆总行程完成货物的派送任务。TSP问题是VRP问题的特例。
车间作业调度问题(JSP)
车间调度问题:存在个工作和台机器,每个工作由一系列操作组成,操作的执行次序遵循严格的串行顺序,在特定的时间每个操作需要一台特定的机器完成,每台机器在同一时刻不能同时完成不同的工作,同一时刻同一工作的各个操作不能并发执行。如何求得从第一个操作开始到最后一个操作结束的最小时间间隔。
总结:
标记的算法需要系统的学一学,在实践一下,其他算法需要了解一下,知道这些个算法有什么作用,比赛期间遇到了,能回忆起来即可,我个人认为建模方法不需要你完全记忆下来,只需要知道两个东西 建模方法的名字 以及用途就可以了因为数模比赛是开卷的形式,可以查阅资料的,但是做这类题目过硬的算法基础
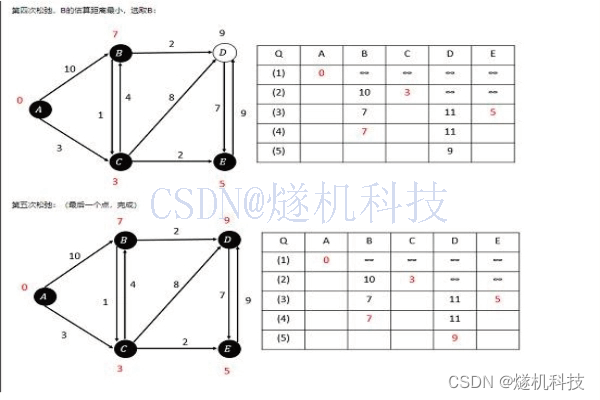
如果遇到图论的题,一般绕不开下面的这些算法
包括DFS,BFS,树与图的深度优先遍历,树与图的广度优先遍历,拓扑排序,Dijkstra,bellman-ford,spfa,Floyd,Prim,Kruskal,染色法判定二分图
如果考到动态规划的题,一般不会特别困难,因为动态规划的状态转移方程很难想,很复杂。简单的动态规划问题也可以使用暴力求解。