第一篇分治法

●前言

●一、分治法是什么？

1.简要介绍

2.生活实例

●二、分治法的典型案例——硬币问题

1.具体问题

2.代码展示（C++）

3.程序代码结果展示

●总结

前言

简单的来说，算法就是用计算机程序代码来实现数学思想的一种方法。学习算法就是为了了解它们在计算机中如何演算，以及在当今的信息时代，它们是如何在各个层面上影响我们的日常生活的，从而提高我们的逻辑思维能力和处理实际问题的能力。善用算法、巧用算法，是培养程序设计逻辑的重中之重，许多实际的问题都可用多个可行的算法来解决，但是要从中找出最优的解决算法却是一项挑战。

一、分治法是什么？

1.简要介绍

分治法是一种很重要的算法，我们可以用分治法去逐一拆解复杂的问题，使复杂问题简单化。它的核心思想就是将一个难以直接解决的复杂问题依照相同的概念将其分为多个子问题，从而各个击破解决问题。

2.生活实例

① 如果有一幅画它由八部分组成，但是如果直接把这八块看成一个整体的话是很难直接画出实现的，所以我们可以先将其分为2组各四幅来完成。如果还是比较复杂，就再将其分成4组各两幅画去完成...... 直到最终画出每一幅画再将其拼接完整即可

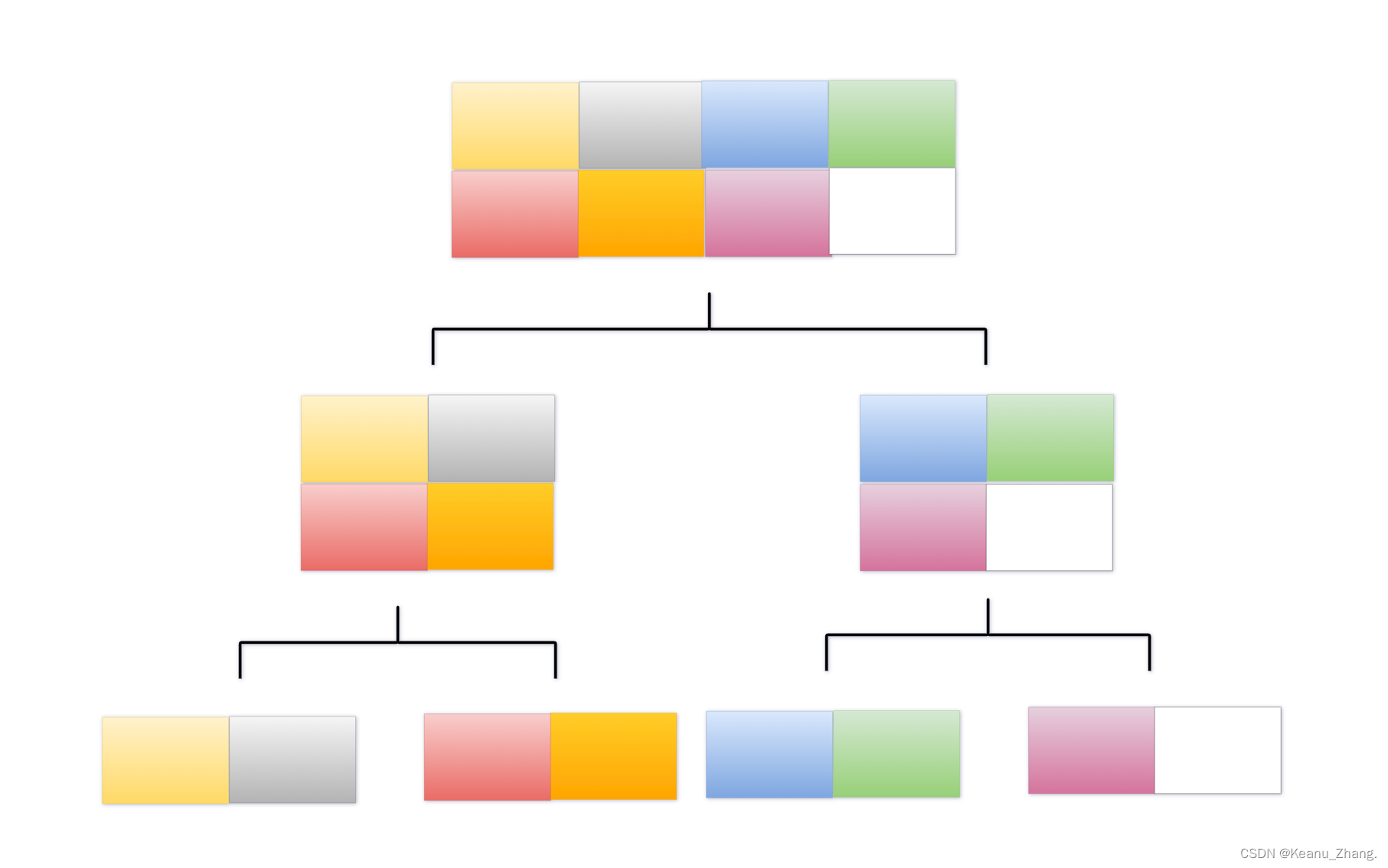
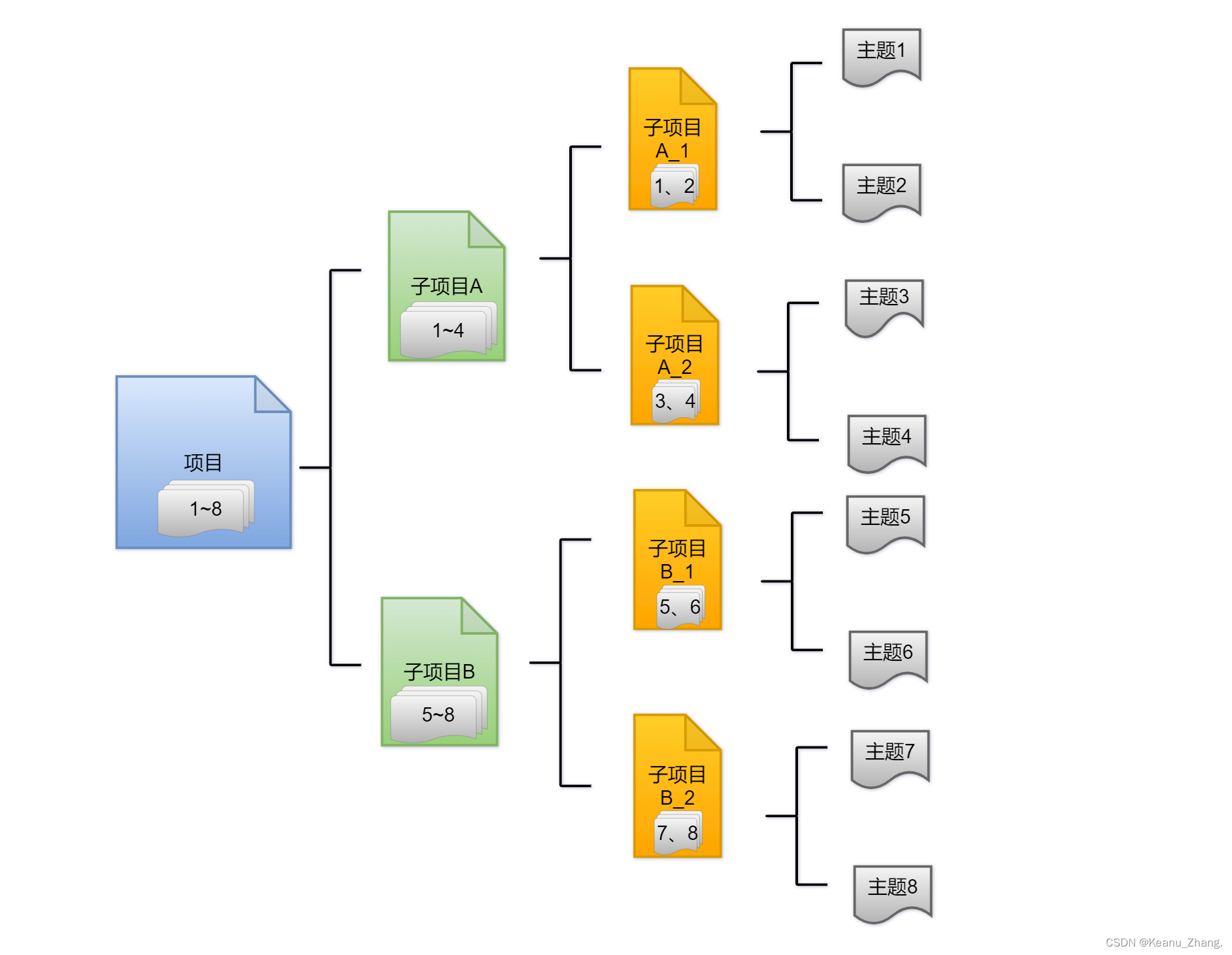
②一个部门被公司去委派去做一个项目规划，这个规划需要8个章节的主题，如果只靠一个人去完成，不仅耗费较长的时间还可能会因为没有去集思广益，从而最终导致项目没有什么亮点而失败。这时我们去用到分治法的核心思想，部门经理将这个大项目分给两个子项目负责人去完成。不过，为了让这个规划更快完成，又能去找到合适的分类，每个子项目负责人再分别将其分派给两个小团队，小团队从而分配给不同的成员去完成。通过这种方法，我们将所需时间缩减到原先一个人独立完成时间的1/8，项目每个章节主题内容也集思广益，从而为企业创造了更大的价值。

二、分治法的典型案例——硬币问题

1.具体问题

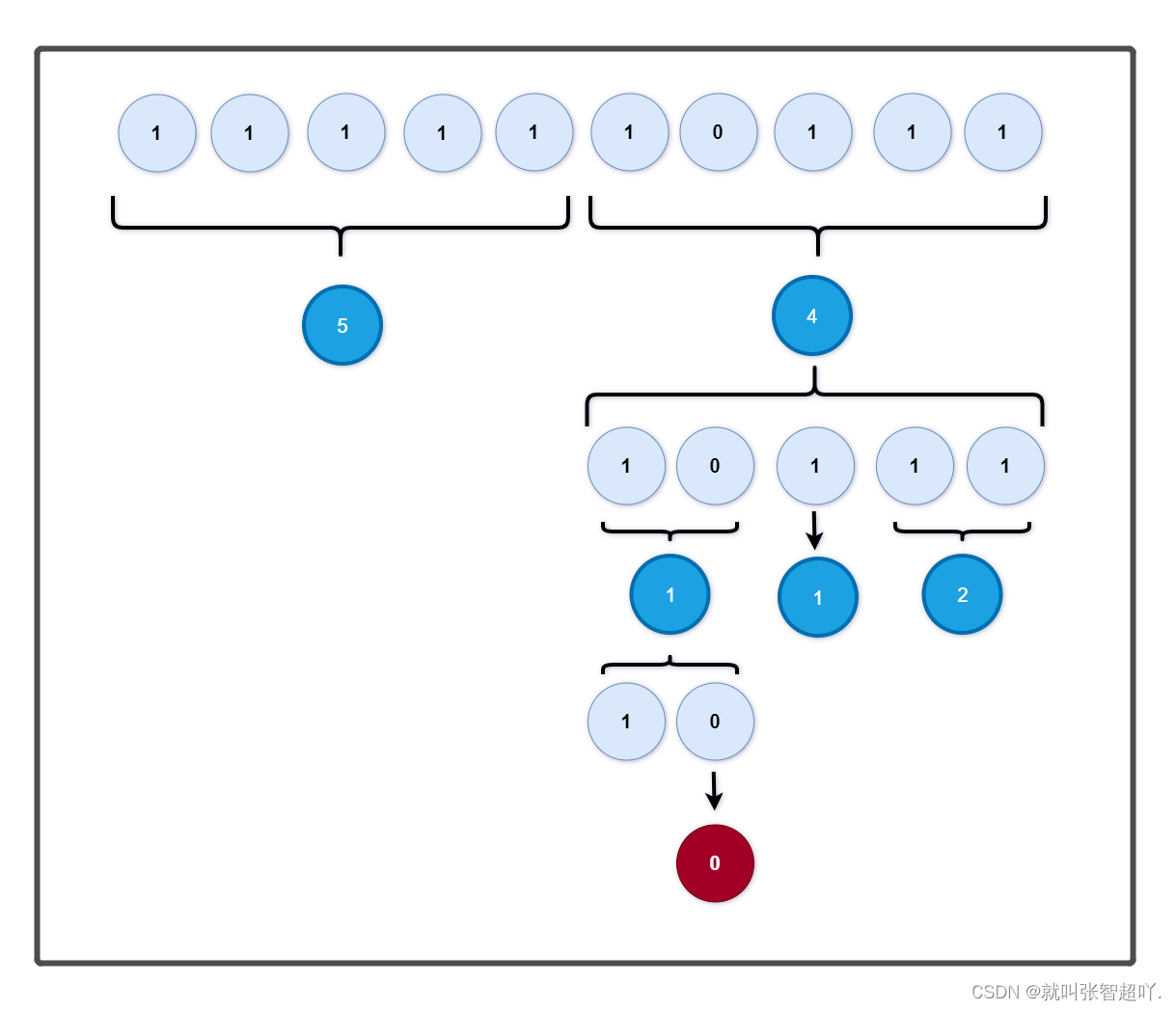
在下面我们将硬币分为1和0两个值，1为真硬币，0为假硬币。分两种情况，偶数枚硬币和奇数枚硬币，并将其随机排成一列，其中有一个假硬币（假硬币位置随机），用分治算法寻找出这枚假硬币所在的位置，如下图所示。

① 当硬币个数为偶数时（10枚）：

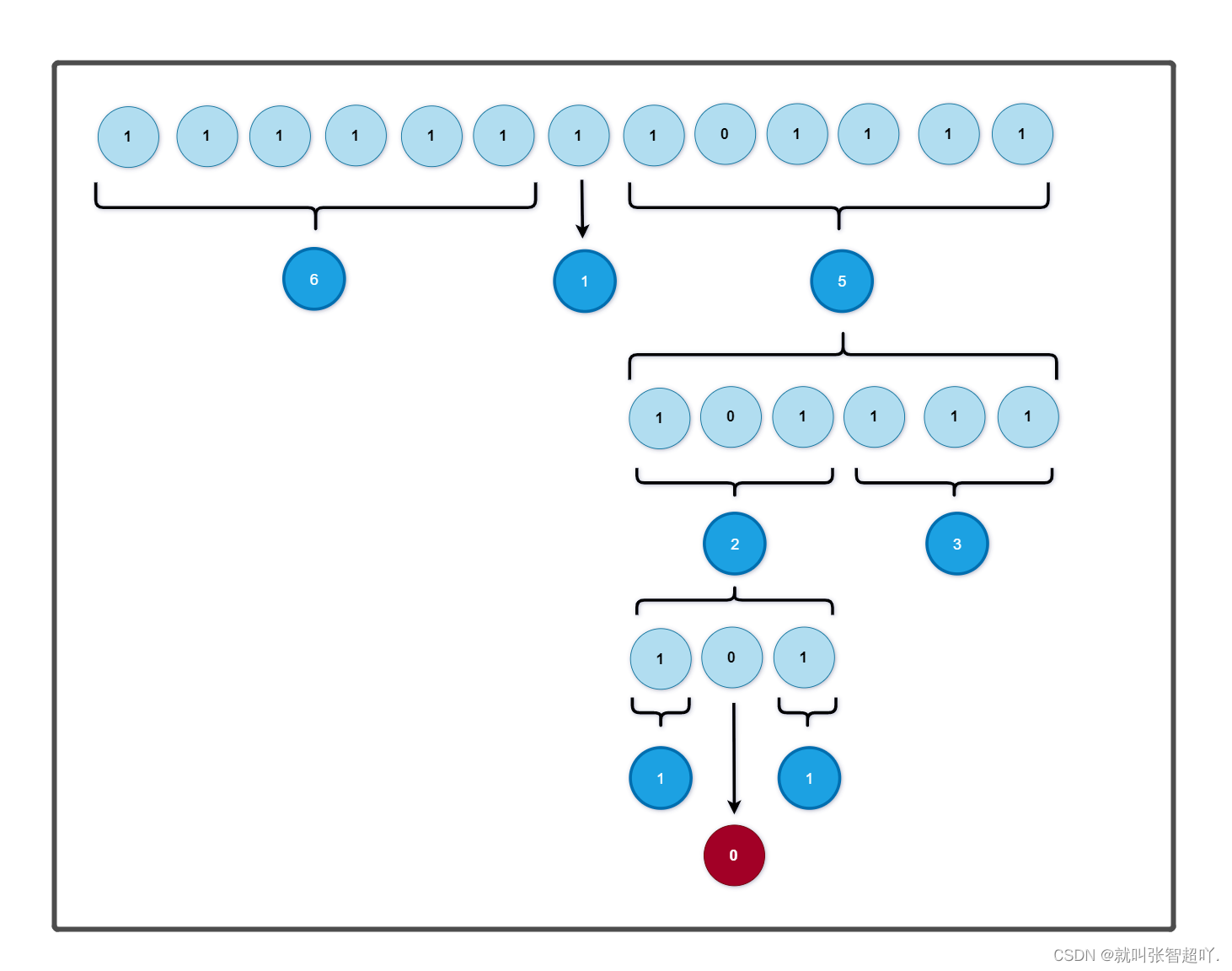
② 当硬币个数为奇数时（13枚）：

2.代码展示（C++）

用程序代码去实现一个功能：输入20枚硬币，其中有一枚假硬币并且位置随机，用分治法的核心思想去找到该枚假硬币所在的位置。

#include<iostream>
using namespace std;
#define maxsize 20  //硬币的数目
class fenzhi {
public:
	int falsecoin(int low, int high);
	void showresult();
	int num;
	int coin[maxsize];
	int result;
};
int fenzhi::falsecoin(int low, int high)
{
	int sum1=0;
	int sum2=0;
	int sum3=0;
	if (low + 1 == high)  //只有两枚硬币
	{
		if (coin[low] < coin[high])
		{
			result = low + 1;
			return result;
		}
		else
		{
			result = high + 1;
			return result;
		}
	}	
	//分治算法
	 if((high-low+1)%2==0)  //n是偶数
	{ 
		for (int i = low; i <= low+(high-low)/2; i++)
		{
			sum1 += coin[i];//前半段和
		}
		for (int j = low + (high - low) / 2+1; j <= high; j++)
		{
			sum2 += coin[j];//后半段和
		}
		if (sum1 > sum2)
		{
			result = falsecoin(low + (high - low) / 2 + 1, high); //递推后半段
			return result;
		}
		else if(sum1 < sum2)
		{
			result = falsecoin(low, low + (high - low) / 2); //递推前半段
			return result;
		}
	}
	 else  //n是奇数
	{
		for (int i = low;i<=low+(high-low)/2-1;i++)
		{
			sum1 += coin[i];   //中位数的前半段和
		}
		for (int j = low + (high - low) / 2+1; j <= high; j++)
		{
			sum2 += coin[j];   //中位数的后半段和
		}
		sum3 = coin[low + (high - low) / 2];   //中位数
		if (sum1 > sum2)      //前半段和大于后半段和
		{
			result = falsecoin(low + (high - low) / 2 + 1, high);//递推后半段
			return result;
		}
		else if (sum1 < sum2)   //前半段和小于后半段和
		{
			result = falsecoin(low, low + (high - low) / 2 - 1);//递推前半段
			return result;
		}
		if (sum1 + sum3 == sum2 + sum3)    //前半段和加中位数等于后半段和加中位数，所以中位数为目标寻找值
		{
			result = low + (high - low) / 2+1;
			return result;
		}
	}
}
void fenzhi::showresult()
{
	cout << "假币所在的位置：" << this->result << endl;
}
void text()
{
	fenzhi fz;
	cout << "输入硬币的总数目：" << endl;
	cin >> fz.num;
	cout << "请输入硬币的真假（1真/0假）：" << endl;
	for (int i = 0; i < fz.num; i++)
	{
		cin >> fz.coin[i];
	}
	fz.falsecoin(0, fz.num - 1);
	fz.showresult();
}
int main()
{
	text();
}

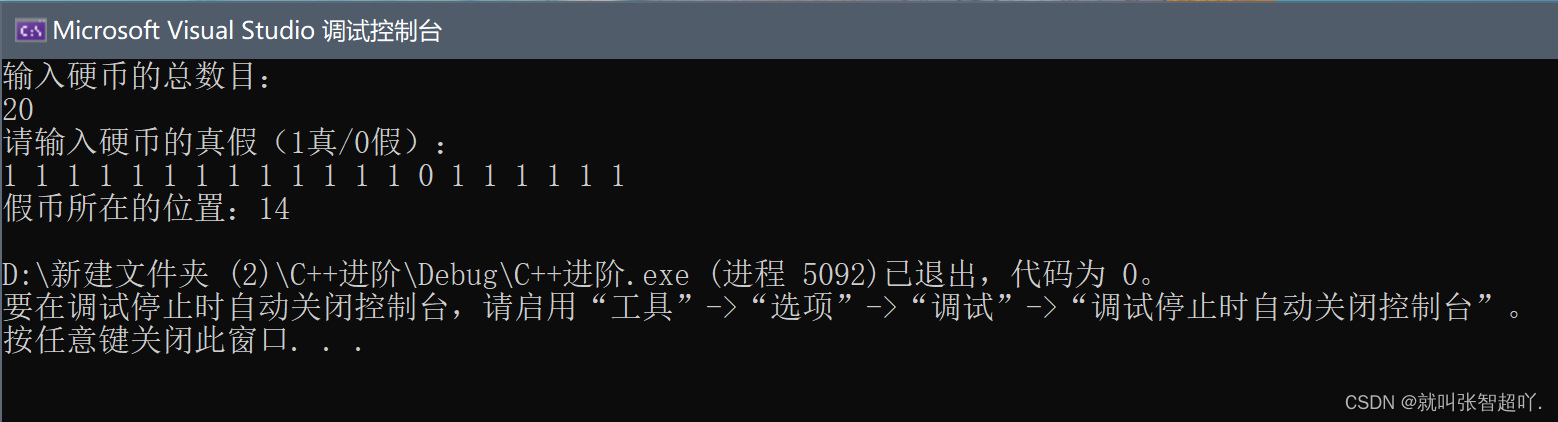
3.程序代码结果展示

总结

通过分治法可以让原来无序、复杂的问题变成一个规则、简单，数量少，速度快并且更容易解决的小问题。其实任何一种可以用程序来求解的问题，所需的计算时间都与其规模和复杂度有关，问题规模越小，越容易直接去进行求解，从而可以去不断分解问题，使子问题规模去不断缩小，让这些子问题简单到可以直接解决，最终进行合并从而解决整个问题。