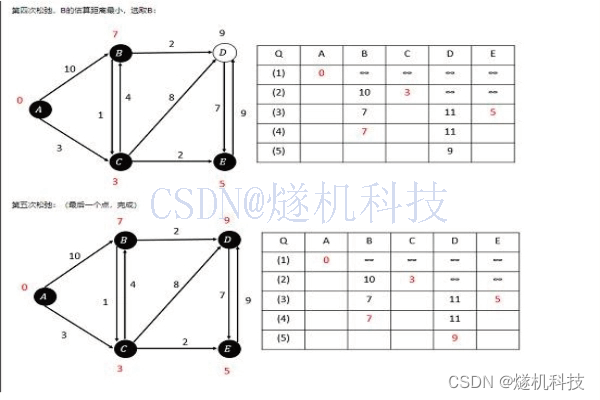
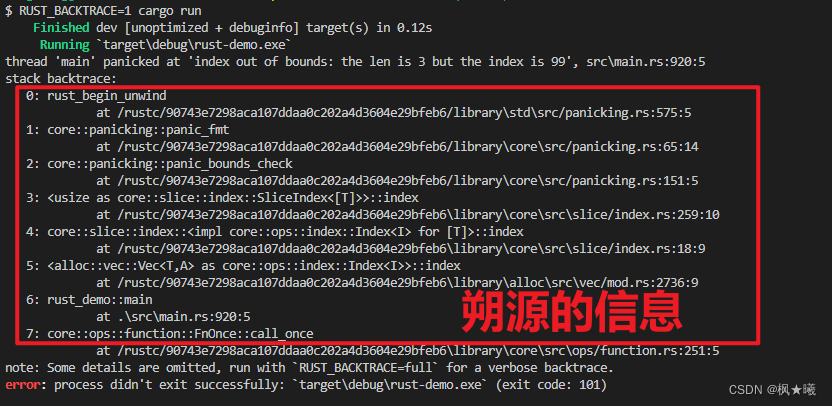
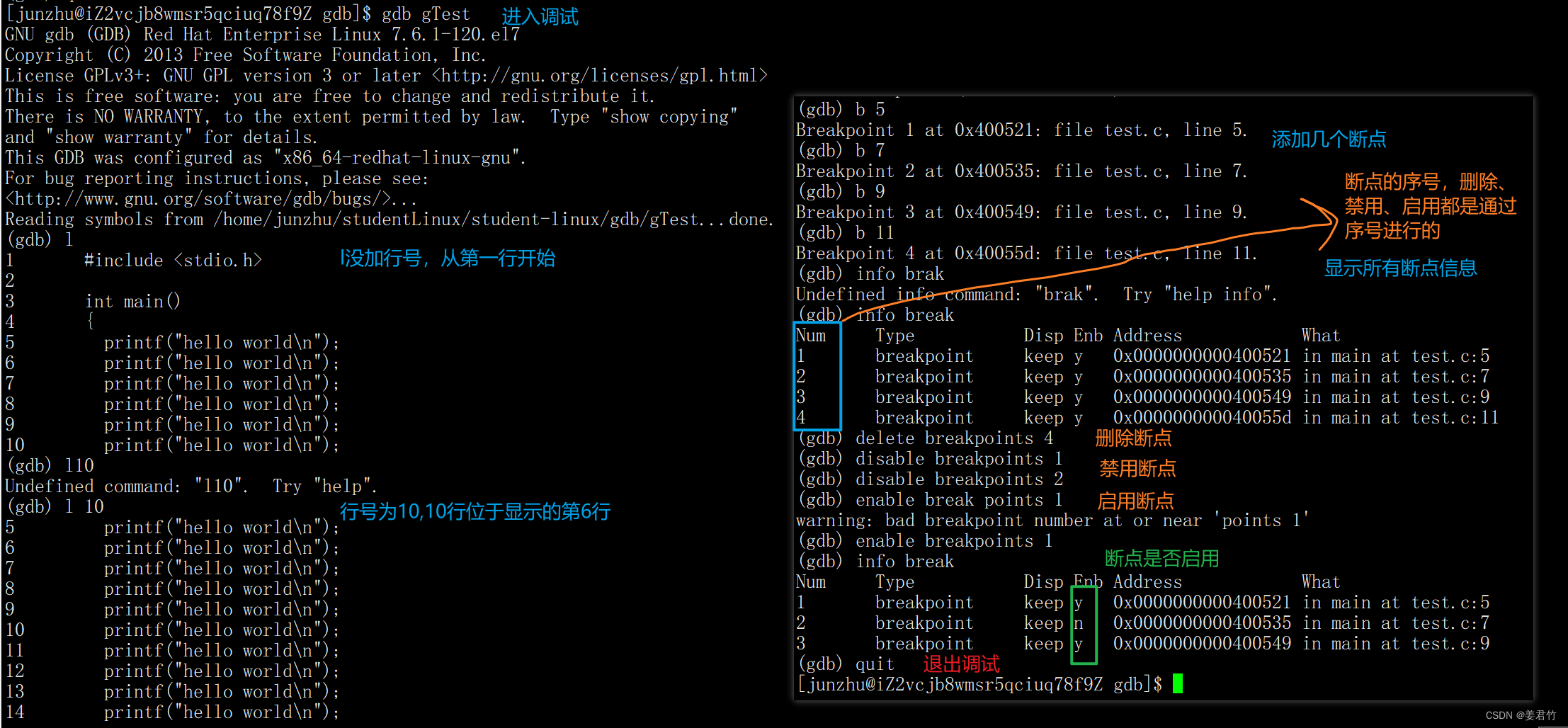
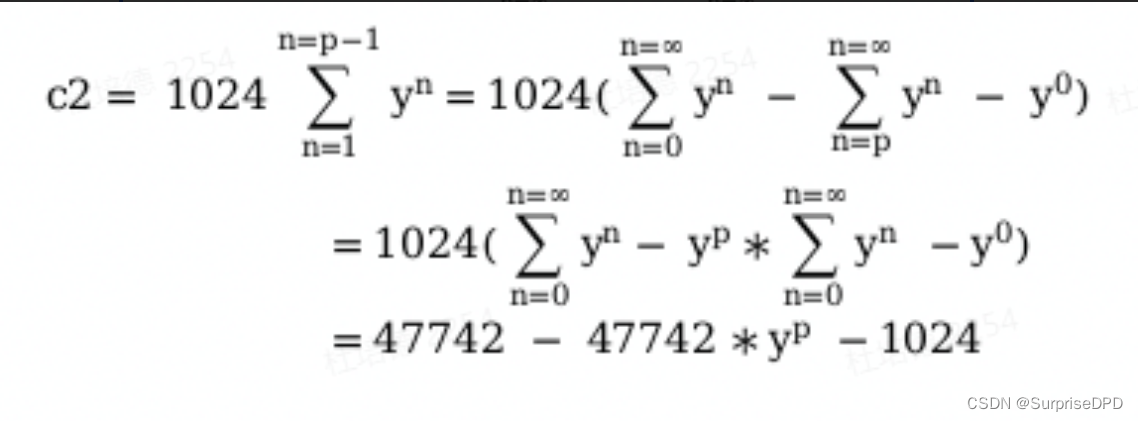一共经过了5次迭代。

第1次迭代的设计思路：

强化学习demo游戏“cartpole”重述

游戏目标：向左/右移动小车cart，保证杆pole始终在小车上方，是大多数强化学习入门教材都会介绍的一个经典案例。

强化学习要素分析：

智能体agent：小车cart

行为action：向左/右移动小车

环境environment：小车位置和速度、杆角度和角速度

回报reward：如果经过这个动作后杆在水平线上（也可以简化为偏移竖直线15°以上）回报1，否则回报0

使用强化学习的角度可以将问题理解为：在环境观察值（environment observation）（即小车位置和速度、杆角度和角速度）确定的情况下，对下一步action进行预测。

解决方案为建立一个Q表q-learning（强化学习论文中常出现的一个term，即key-value组合，类似python的dict字典，java的map等），key是环境观察值和行为action集合，value是下一步action的预测。这个简单案例的行为集合始终为向左/右移动小车。

所以，当这个Q表很完善的时候，AI玩游戏时即可通过这个表的key找到对应的value，做出合理决策。

训练开始。引入epsilon-greedy算法，该算法有类似遗传算法的特征，包括经验和试错两部分。经验即按Q表进行决策，如果没有游戏结束则给以奖励1，使得相应行为action的概率增加。试错即以设置的epsilon概率随机决策，同样，如果没有游戏结束则给以奖励1，使得相应行为action的概率增加。

一开始Q表为空，在对当前环境key找不到对应的value时随机决策。

论文上截取的公式

公式中s为当前的环境观察值，a为行为action，alpha为学习率（与深度学习的学习率概念相同，这里不做详细介绍），r为回报reward，s’、a’为决策后下一时刻的环境和行为，gamma为discount factor，即未来回报的衰减比例。

经过约10000次训练，Q表就可以完善。

这里的Q表对于环境较为简单的场景可以使用这种key-value集合的方式表达输入和输出。对于复杂的环境，可以将Q表替换为模型。例如，这个环境也可以将Q表替换为一个输入维度为4、输出维度为1的BP神经网络，经过若干轮迭代后，也可以达到类似的效果。

下面讨论OD寻找最优路径的案例（以下简称“本案例”）。

按照上述demo的样子，假设这个问题要用强化学习的思路解决。

任务目标：给定一个路网拓扑关系邻接矩阵表和当前时刻的路网平均速度，针对一个O点和D点，寻找行程时间最短的最优路径。

强化学习要素分析：

智能体agent：车辆

行为action：在每个决策点选择车的方向，例如十字路口向前/左/右开车

环境environment：路网平均速度

回报reward：行程时间

设想的解决方案：车辆一开始在O点，仿真系统根据当前的路网平均速度预测出下一个决策点（即时间戳）路网的状态，经过若干次预测后，得到当前时刻下采取不同行为进行决策时O点到D点的行程时间，作为“回报函数”让小车进行决策，往下一步进行一个action，然后继续循环……另外，中间也可以以一定概率随机决策，……

问题点：

1. 本案例的仿真系统没有能力预测下一个或下若干个（取决于O点和D点的距离）决策点的路网状态。仅根据当前时刻路网的平均速度和路网拓扑结构，远不足以预测未来路网的平均速度状态。

2. 更重要的，本案例的车辆没有强化学习的特征。很明显，车辆没有一个类似于Q表或神经网络模型的一个强化学习模块，而是使用类似贪心算法的一步一步找最佳方向进行决策的思想。车辆不像强化学习概念中的智能体（agent，一开始没有智能，通过不断的与环境进行交互使得其越来越智能，可以根据当前环境状态得知下一步该做什么），车辆的第一步决策是根据仿真系统给的行程时间决定的，第n步决策仍然是根据仿真系统给的行程时间决定的，并没有给车辆更新什么Q表或模型权重，不断的“交互”其实并没有让车辆变得越来越智能。

3. “深度强化学习”指算法的强化学习模块使用深度学习的方法替代Q表，智能体在不断的与环境进行交互的过程中不断训练这个深度学习网络使得智能体越来越智能，而不是说仿真模块里用了一下LSTM或者其他什么模型预测下一个决策点的路网速度就叫“深度强化学习”了。

综上所述，我们认为使用强化学习方法解决本案例只是从某些所谓“A类顶刊、顶会、发明专利”中找的“灵感”并将别人的一些算法、demo“结合”起来套用的结果，仔细分析相关论文和代码之后，认为“目前全球还没有人想到深度强化学习可以解决OD行程时间最优化问题”是因为这个问题与AlphaGo下棋、自动驾驶、Atari小游戏等案例具有本质的明显不同。强化学习不是一个很新的概念，其实这个数据也不是很难找（openstreetmap可以获得路网link拓扑关系，高德api可以提供路网平均速度等）建议团队更换思路，寻找更合适的方法解决问题。

 

第2次迭代的设计思路：

任务目标：给定一个路网拓扑关系邻接矩阵表和若干个时刻的路网平均速度，针对一个O点和D点，寻找行程时间最短的最优路径。

强化学习要素分析：

智能体agent：车辆

行为action：在每个决策点选择车的方向，例如十字路口向前/左/右开车

环境environment：路网平均速度、路网的拓扑关系

回报reward：给定的action是否为最优

设想的解决方案：车辆一开始在O点，随机选择一个方向行驶，仿真系统根据给定的若干个时刻的路网平均速度使用dijkstra算法计算出O点到D点的最短路径，如果仿真系统给定的这个最短路径的第一步前进方向dijkstra算法的结果相同，则reward为1，否则为0。选定不同的O点和D点，经过若干次更新权重后，得到一个决策模型，这个神经网络模型的输入为（O点、D点、当前时刻路网平均速度、路网拓扑关系、可选的action的集合），输出为（选择不同的action的概率，即下一步的决策）。

神经网络的输入

O/D点：使用所在的道路ID表示/使用所在的经纬度表示？

这一刻的路网平均速度：如果路网有n个link，则作为n维特征输入

路网的拓扑结构：邻接矩阵输入神经网络

可选的action集合

神经网络的输出

输出一个

action_set={“向前”, “向左”, “向右”}的情况

{

“向前”: 0.8,

“向左”: 0.1,

“向右”: 0.1

}

action_set={“向前”, “向左”}的情况

{

“向前”: 0.7,

“向左”: 0.3

}

这样格式的结果

第3次迭代的设计思路：

任务目标：给定一个路网拓扑关系邻接矩阵表和若干个时刻的路网平均速度，针对一个O点和D点，寻找行程时间最短的最优路径。

强化学习要素分析：

智能体agent：车辆

行为action：在每个决策点选择车的方向，例如十字路口向前/左/右开车

环境environment：路网平均速度、路网的拓扑关系

回报reward：给定的action是否为最优

设想的解决方案：车辆一开始在O点，随机选择一个方向行驶，仿真系统根据给定的若干个时刻的路网平均速度使用dijkstra算法计算出O点到D点的最短路径，如果仿真系统给定的这个最短路径的第一步前进方向dijkstra算法的结果相同，则reward为1，否则为0。选定不同的O点和D点，经过若干次更新权重后，得到一个决策模型，这个神经网络模型的输入为（O点、D点、当前时刻路网平均速度、路网拓扑关系、可选的action的集合），输出为（选择不同的action的概率，即下一步的决策）。

神经网络的输入

输入是一个向量，这个向量由以下属性拼接而成：

1. 车辆当前位置：车辆当前位置是一个路网中的节点node，使用所在交叉口的相邻的道路link的ID表示，即在邻接矩阵中的行/列号（2维）

2. D点：同上，节点node使用所在交叉口的相邻的道路link的ID表示，即在邻接矩阵中的行/列号（2维）

3. 路网的拓扑关系：将图邻接矩阵转换为线性表（n*n维）

4. 路网当前时刻速度（n维）

神经网络的输出

输出为3个维度，分别为向前、向左和向右

设计流程

1. 建立2个空表，列分别为车辆训练集的特征值和目标值

2. 选定路网中一个O点和D点，将当前的速度和OD点位置作为这次训练的特征值，将目标值定为三种action均为1/3。针对当前的速度，使用dijkstra算法计算正确的最短路径，将这个最短路径的第一步对应的action的权重提高，将另两种action的权重降低。

3. 对不同时刻的速度观察值、不同OD点进行2. 中的计算，不断更新训练集，计算约数万条。

4. 使用2. 中的方法生成测试集。将训练好的模型保存，并把测试集的特征值输入神经网络，与测试集的目标值进行对比，得出模型的评价结果。

存在的问题

1. Dijkstra并不知道自己决策的路径是向哪个方向，只知道下一条要走的路id是多少，邻接矩阵数据集也无法获取是哪个方向

2. 方向可能不是一直都是3个，可能有的节点只能向前走，也可能是3个以上方向，如可以向后、是环道等，强化学习要求action集合必须有限、确定，无法表示

3. 经过查询资料，并没有“将图数据结构转化为线性表”的算法，如果只是把图的邻接矩阵一行一行并排的话神经网络学不到图拓扑结构的特征

第4次迭代的设计思路：

任务目标：给定一个路网拓扑关系邻接矩阵表和若干个时刻的路网平均速度，针对一个O点和D点，寻找行程时间最短的最优路径。

强化学习要素分析：

智能体agent：车辆

行为action：在每个决策点选择车的方向，例如十字路口向前/左/右开车

环境environment：路网平均速度、路网的拓扑关系

回报reward：给定的action是否为最优

设想的解决方案：车辆一开始在O点，随机选择一个方向行驶，仿真系统根据给定的若干个时刻的路网平均速度使用dijkstra算法计算出O点到D点的最短路径，如果仿真系统给定的这个最短路径的第一步前进方向dijkstra算法的结果相同，则reward为1，否则为0。选定不同的O点和D点，经过若干次更新权重后，得到一个决策模型，这个神经网络模型的输入为（O点、D点、当前时刻路网平均速度、路网拓扑关系、可选的action的集合），输出为（选择不同的action的概率，即下一步的决策）。

神经网络的输入

输入是一个向量，这个向量由以下属性拼接而成：

1. 车辆当前位置O点：车辆当前位置是一个路网中的节点node，使用所在交叉口的相邻的道路link的ID表示，即在邻接矩阵中的行/列号（2维）

2. D点：同上，节点node使用所在交叉口的相邻的道路link的ID表示，即在邻接矩阵中的行/列号（2维）

3. 路网当前时刻速度（n维）

神经网络的输出

输出为p个维度，p为所有node相邻node的数量的最大值

设计流程

1. 建立2个空表，列分别为车辆训练集的特征值和目标值。特征值表的特征包括（车辆当前位置O点-2维、D点-2维、路网当前时刻速度-n维）

2. 选定路网中一个O点和D点，将当前的速度和OD点位置作为这次训练的特征值。如果当前O点位置可以一步action到达的下一个node的数量为p，那么将目标值p维的数值均填充为1/p，即相同的概率；如果上述数量为q（小于p），则将目标值前q维设置为1/q，后p-q维设置为0。使用注意力机制获取神经网络输入值之间隐含的关系。针对当前的速度，使用dijkstra算法计算正确的最短路径，将这个最短路径的第一步对应的action的权重提高，将其他概率不为0的action的权重降低。

3. 对不同时刻的速度观察值、不同OD点进行2. 中的计算，不断更新训练集，计算约数万条。

4. 使用2. 中的方法生成测试集。将训练好的模型保存，并把测试集的特征值输入神经网络，与测试集的目标值进行对比，得出模型的评价结果。

存在的问题

1. 比如说路网如下图（以树形结构简化为例）：

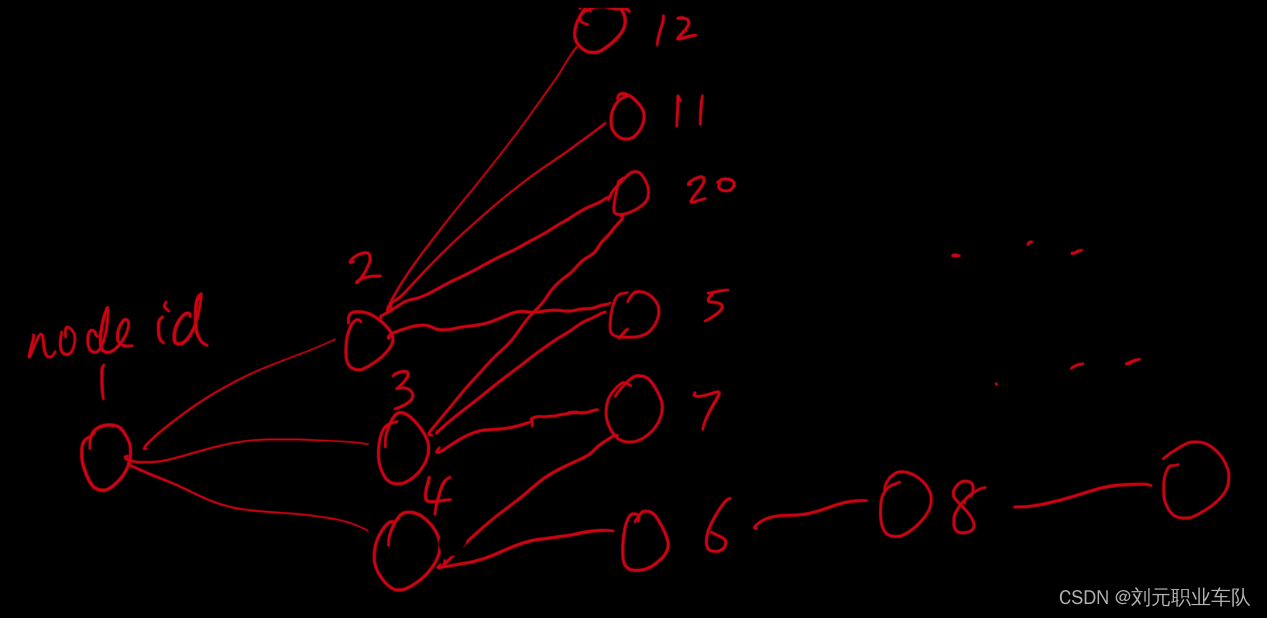
如果将目标值按照上述方法排列的话，神经网络输出值如下表：

Node id	邻接1	邻接2	邻接3	邻接4
1	下一步选择Node 2的概率	下一步选择Node 3的概率	下一步选择Node 4的概率	0
2	下一步选择Node 12的概率	下一步选择Node 11的概率	下一步选择Node 20的概率	下一步选择Node 5的概率
3	下一步选择Node 20的概率	下一步选择Node 5的概率	下一步选择Node 7的概率	0
4	下一步选择Node 7的概率	下一步选择Node 6的概率	0	0
6	下一步选择Node 8的概率	0	0	0
…	…	…	…	…

神经网络的输出（输入也是这样）中。每个维度应该是代表一个“目标值”，也就是“邻接1”、“邻接2”…这些分别都是每一行输入的不同特征对应的不同目标值的“预测结果”，就好比“输入一个地区的人口、车辆保有量、面积、财政收入…特征，输出这个地区的GDP、人均收入…”一样。而这个案例的设计中，邻接1、2、3、4是4种不同的选择，“邻接1”、“邻接2”不是独立的目标值。每一行特征是选择第一个预测结果还是第2,3,4个预测结果没有什么特点，属于平行的东西，每个节点的“邻接1,2，…”打乱交换一下本质上也没变什么，但是神经网络这样设计的话输出值完全就变了。

另外还有注意力机制，怎么起到让神经网络看出类似邻接关系的作用也不能理解

 

第5次迭代的设计思路：

任务目标：给定一个路网若干个时刻的路网平均速度，针对一个O点和D点，寻找行程时间最短的最优路径。

强化学习要素分析：

智能体agent：车辆

行为action：在每个决策点选择车的方向，例如十字路口向前/左/右开车

环境environment：路网平均速度、路网的拓扑关系

回报reward：给定的action是否为最优

设想的解决方案：车辆一开始在O点，随机选择一个方向行驶，仿真系统根据给定的若干个时刻的路网平均速度使用dijkstra算法计算出O点到D点的最短路径，如果仿真系统给定的这个最短路径的第一步前进方向dijkstra算法的结果相同，则reward为1，否则为0。选定不同的O点和D点，经过若干次更新权重后，得到一个决策模型，这个神经网络模型的输入为（O点、D点、当前时刻路网平均速度、路网拓扑关系、可选的action的集合），输出为（选择不同的action的概率，即下一步的决策）。

神经网络的输入

输入是一个向量，这个向量由以下属性拼接而成：

1. 车辆当前位置O点：车辆当前位置是一个路网中的节点node，使用所在交叉口的相邻的道路link的ID表示，即在邻接矩阵中的行/列号（2维）

2. D点：同上，节点node使用所在交叉口的相邻的道路link的ID表示，即在邻接矩阵中的行/列号（2维）

3. 路网当前时刻速度（n维）

神经网络的输出

输出为3个维度，分别为向前、向左、向右

设计流程

1. 建立2个空表，列分别为车辆训练集的特征值和目标值。特征值表的特征包括（车辆当前位置O点-2维、D点-2维、路网当前时刻速度-n维）

2. 选定路网中一个O点和D点，将当前的速度和OD点位置作为这次训练的特征值。如果当前O点位置可以一步action到达的下一个node的数量为p，那么将目标值p维的数值均填充为1/p，即相同的概率；如果上述数量为q（小于p），则将目标值前q维设置为1/q，后p-q维设置为0。使用注意力机制获取神经网络输入值之间隐含的关系。针对当前的速度，使用dijkstra算法计算正确的最短路径，将这个最短路径的第一步对应的action的权重提高，将其他概率不为0的action的权重降低。

3. 对不同时刻的速度观察值、不同OD点进行2. 中的计算，不断更新训练集，计算约数万条。

4. 使用2. 中的方法生成测试集。将训练好的模型保存，并把测试集的特征值输入神经网络，与测试集的目标值进行对比，得出模型的评价结果。

最终解决了问题。