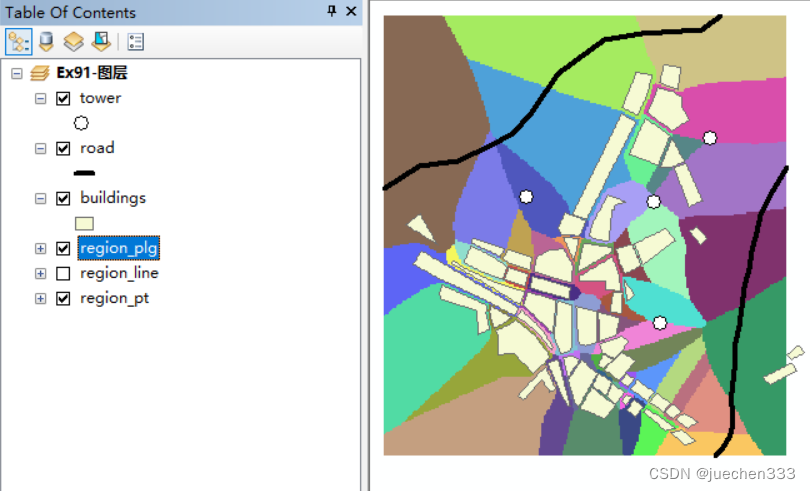
1.二分图最大匹配

        设G为二分图,若在G的子图M中，任意两条边都没有公共节点,那么称M为二分图G的一组匹配。在二分图中，包含边数最多的一组匹配称为二分图的最大匹配。
        交替路:从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
        增广路:从一个未匹配点出发，走交替路，若能到达另一个未匹配点，则这条交替路称为增广路。
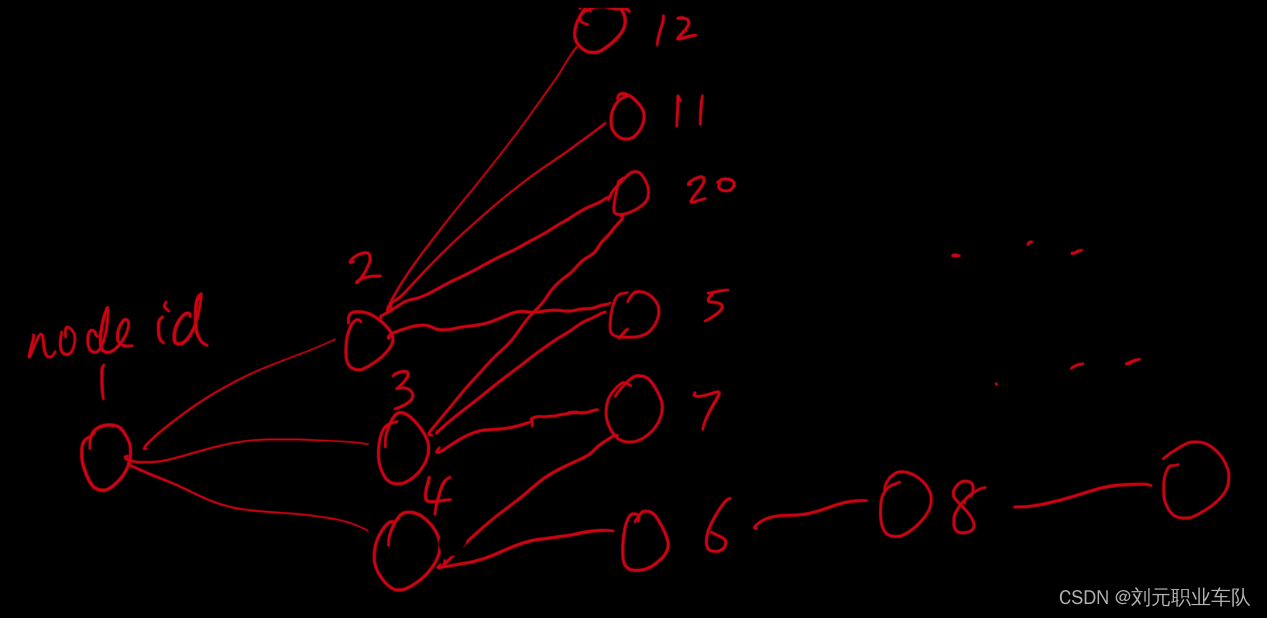
例如，3一5→1→4→2—7
        观察增广路,我们会发现:非匹配边比匹配边多一条。只要把增广路中的匹配边和非匹配边的身份交换（即倒过来走)，交换后，图中的匹配边数目比原来多了1条。这里的增广路就是指能增加匹配边的一条路。
        匈牙利算法:通过不停地找增广路来增加匹配边。找不到增广路时，达到最大匹配。可以用DFS 或BFS 来实现。

 具体过程就是，对于集合A,B。

1.首先，枚举A集合的元素:1,2,3

2.对于A集合的每个元素i,枚举能够B集合中能够与i配对的元素j。比如上图的1，能够配对的有4,5,6.

• 若j还未配对，则配对
• 若j已经标记为不能再访问，则跳过
• 若j已经配对，但与j配对的元素还能够与其他元素配对，则让出，让i进行配对
• 否则，枚举下一个能够配对的元素

3.枚举完所有能够与i进行配对的元素后，都不能进行配对，则返回False

2.有权二分图的匹配问题<