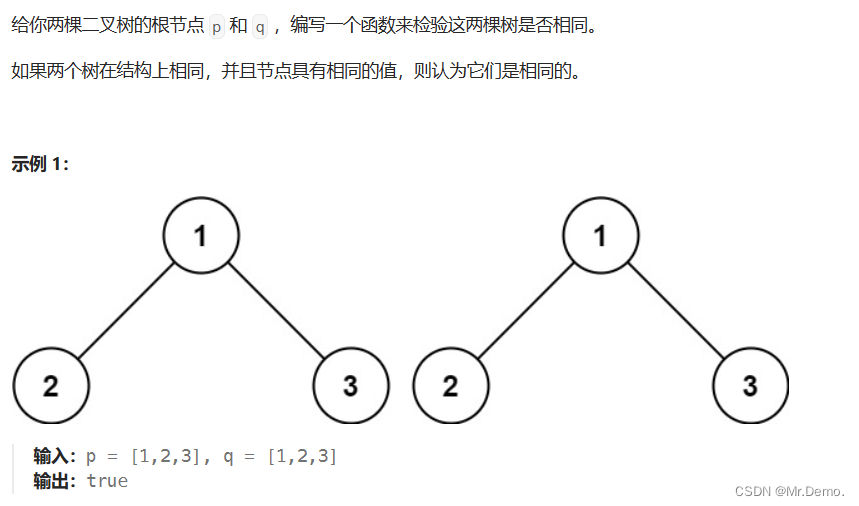
1. 判断是否为相同的二叉树
OJ链接
public boolean isSameTree(Node p, Node q) {
if (p == null && q != null || p != null && q == null){//结构不同
return false;
}
if (p == null && q == null){//结构相同,都是空树
return true;
}
if (p.value != q.value){//结构相同,不是空树,但是值不一样
return false;
}
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);//向下递归
}
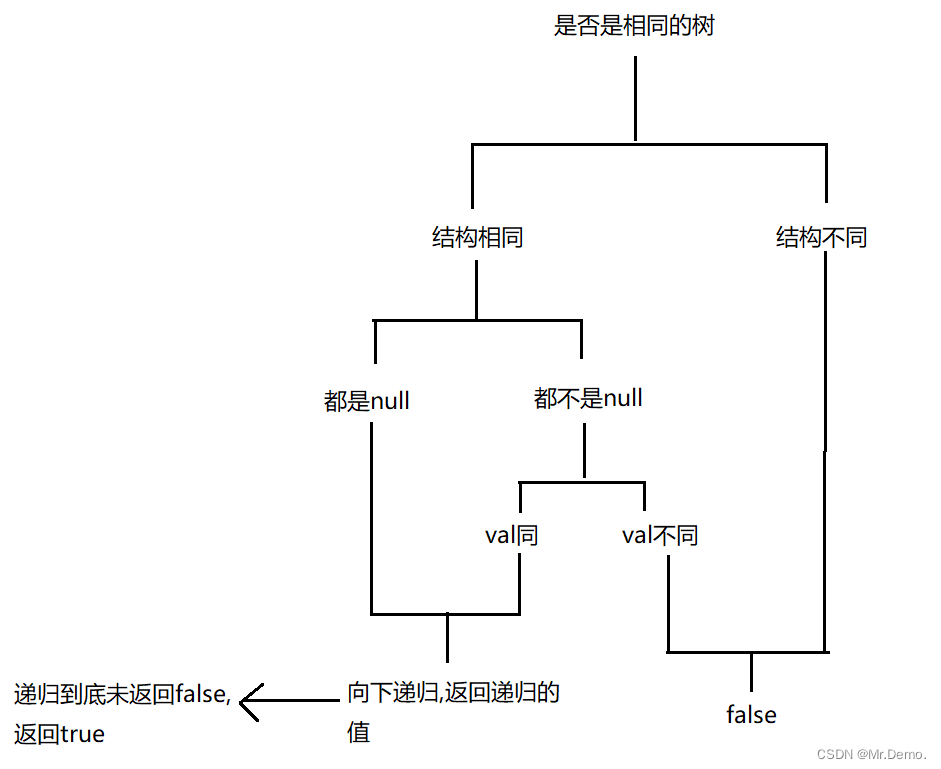
整体思路:
首先判断结构是否相同,一种是不同,这种直接返回false,另一种是相同,一种是都为空,这种直接返回true,一种是都不为空相同,那么进行下一步,判断值是否相同,相同向下递归,不相同返回false.
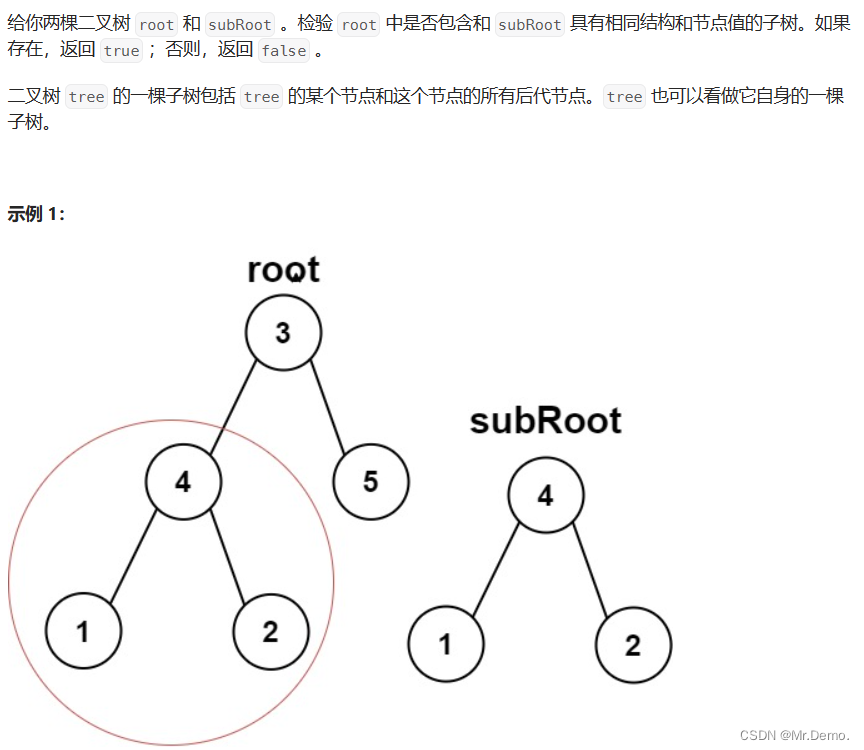
2. 判断是否为子树
OJ链接
public boolean isSubtree(Node root, Node subRoot) {
if (root == null){//所给的树可能是空树,在下一步只是判断,并没有真正拦截空树,在第三个条件就报了空指针异常
return false;
}
if (isSameTree(root,subRoot)){//从根节点判断是否相同
return true;
}
if (isSubtree (root.left,subRoot)){
return true;
}
if (isSubtree (root.right,subRoot)){
return true;
}//向下递归,判断左右子树是否与所给树相同
return false;
}
public boolean isSameTree(Node p, Node q) {
if (p == null && q != null || p != null && q == null){//结构不同
return false;
}
if (p == null && q == null){//结构相同,都是空树
return true;
}
if (p.value != q.value){//结构相同,不是空树,但是值不一样
return false;
}
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);//向下递归
}
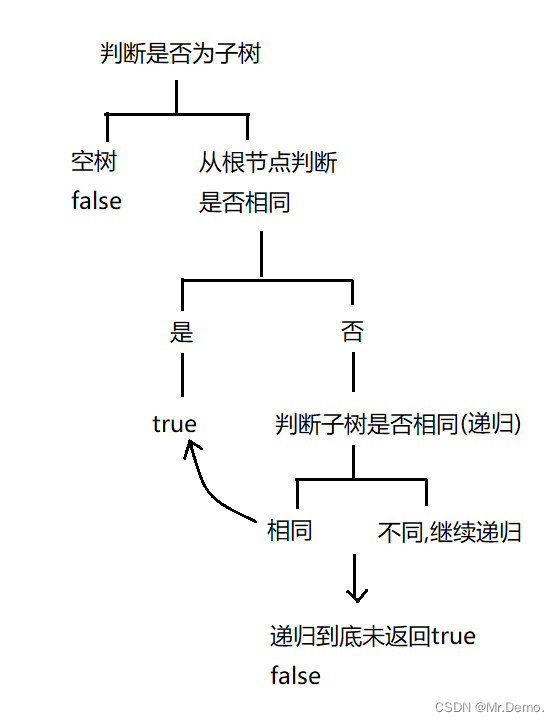
整体思路:
首先判断根结点是否为空,如果为空,返回false,之后从根节点判断两棵树是否是相同的树,如果是,返回true,如果不是,则向左子树和右子树递归,判断左子树和右子树是否和所给的树相同.
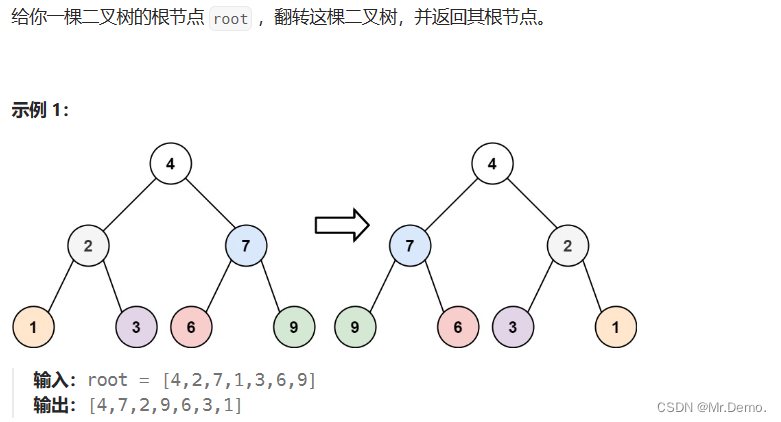
3. 翻转二叉树
OJ链接
public Node invertTree(Node root) {
if (root == null){
return null;//空树返回null
}
Node tmp = null;
tmp = root.left;
root.left = root.right;
root.right = tmp;//交换左结点和右结点
invertTree(root.left);
invertTree(root.right);//向下递归
return root;//返回根节点
}
这里需要注意的一点就是需要引入第三个结点来交换两个结点的位置.只要想到这一点,问题便不是很大.
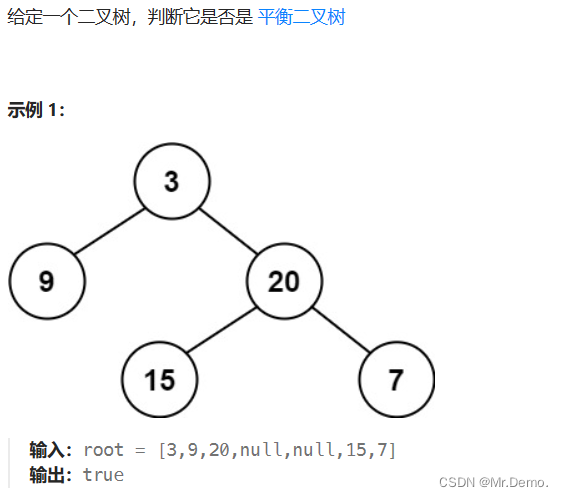
4. 判断是否是平衡二叉树
该题为字节跳动面试真题
OJ链接
- 普通解法
public boolean isBalanced(Node root) {
if(root == null){//空树返回true
return true;
}
int hightleft = getHeight(root.left);
int hightright = getHeight(root.right);//获取两棵树的高度,这里设置两棵树的高度是有必要的
//如果不保存这里的值,后面会又很多重复获取高度的操作,效率会大大降低
if(Math.abs(hightleft-hightright)<2 && isBalanced(root.left)
&& isBalanced(root.right)){//根结点所在的树和以左子树右子树为根节点的树都符合条件
return true;
}else{
return false;
}
}
public int getHeight(Node root) {
if (root == null){
return 0;
}
return Math.max(getHeight(root.left),getHeight(root.right))+1;
}
递归思路如图:
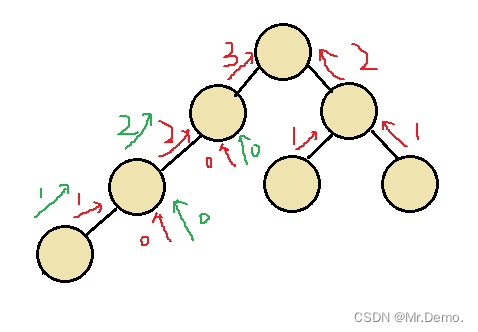
在图中我们可以看到在从根节点递归到作左树的根结点的时候,就已经遇到了不平衡,但是在传入左树的根节点的时候,还是要向下递归,这种做法就使得每一个结点都要向下递归,时间复杂度达到了O(n2),这样就是多此一举的做法,我们希望遇到不平衡就不再向下递归,这种做法是面试官青睐的做法.
public int getHeight2(Node root){
if (root == null){
return 0;//结点为空返回0
}
int leftHeight = getHeight2(root.left);
int rightHeight = getHeight2(root.right);//获取高度
if (leftHeight>=0 && rightHeight >=0 && Math.abs(leftHeight-rightHeight)<2 ){
return Math.max(leftHeight,rightHeight)+1;//返回的值不是-1或者是左右树高度差小于2,返回可以获取的高度
}else{
return -1;//否者返回-1
}
}
public boolean isBalanced2(Node root) {
if(root == null){
return true;
}
return getHeight(root)>=0;//看root的返回值是否为负数,返回值不为负数,说明平衡,否则不平衡
}
递归思路:
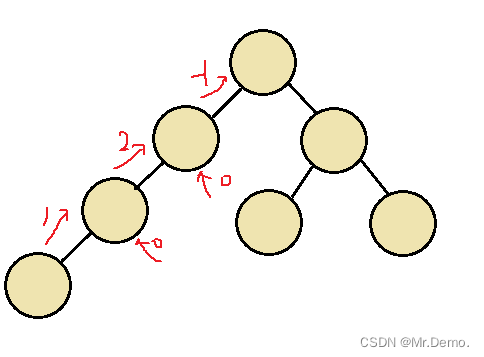
这样的做法就是比较高效的,在从根节点向下递归的时候,如果一旦遇到了不平衡,立即返回-1,对应条件是Math.abs(leftHeight-rightHeight)<2,一旦有一个结点返回了-1,之后的每一个结点在返回的时候均返回-1,对应的是leftHeight>=0 && rightHeight >=0.在最后只需要判断root结点拿到的值是否是-1即可.
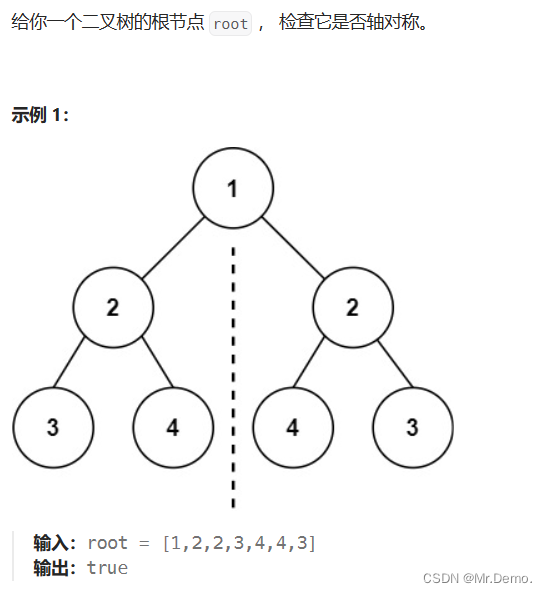
5. 判断是否是对称二叉树
OJ链接
public boolean isSymmetric(Node root) {
if (root == null){
return true;//为空返回true
}
return isSymmetricChild(root.left,root.right);//根节点无需判断,则判断子树是否对称
}
public boolean isSymmetricChild(Node left,Node right){
if (left == null && right == null){
return true;//结构相同,两个都为空,返回true
}
if (left != null && right == null || left == null && right != null){
return false;//结构不同,返回false
}
if (left.value != right.value){
return false;//结构相同,值不一样,返回false
}
return isSymmetricChild(left.left,right.right) && isSymmetricChild(left.right,right.left);
//向下递归,判断左树的左和右树的右,左树的右和右树的左是否相同,不相同返回false
}
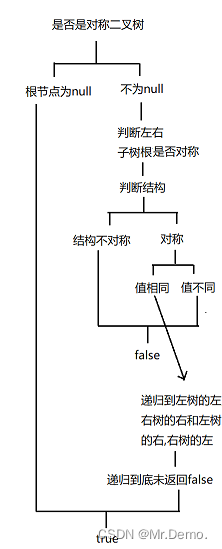
整体思路:
如果这棵树为null,则符合对称树的条件,返回true,之后递归到左右子树,判断左右子树的根节点是否相同(这里判断根结点是否相同的思路和判断两棵树是否是同一棵树的思路相同),如果不同,则返回false,如果相同,则递归左子树的左,右子树的右;左子树的右和右子树的左即可(判断它们是否相同).