目录
前言
递归算法
1、什么是递归算法
2、核心理念
3、代码演示
4、问题探讨:只递不归会怎样?
5、小结
递归实例:汉诺塔问题
1、故事引入
2、移动盘子的逻辑
3、N个盘子的移动分析
4、代码实现N个盘子的移动
5、汉诺塔移动次数计算公式
前言
本文是我关于递归算法的学习记录,完成这篇博客花了大半天的时间,自认为图文结合表述的还算详细,也希望大家阅读后会感到有所帮助;
这篇博客有一些细节的地方完善的不是很好,我日后有更加清晰理解的时候会再优化这篇博客,如果读者有什么不理解的地方,欢迎评论区留言;有写的不对的地方,欢迎批评指正,希望能够完善这篇博客。
递归算法
1、什么是递归算法
定义一个函数,在函数里面调用函数,并且要有结束条件。
2、核心理念
例如:从前有座山,山上有座庙,庙里有个老和尚和小和尚将故事,故事是从前有座山...
递归的核心理念就是函数调用函数,就像故事里面有故事
但是,这个故事并不算一个递归,因为故事只有递(调用自身),没有归(结束条件)
3、代码演示
def f(x):
return x + f(x-1)
print(f(3))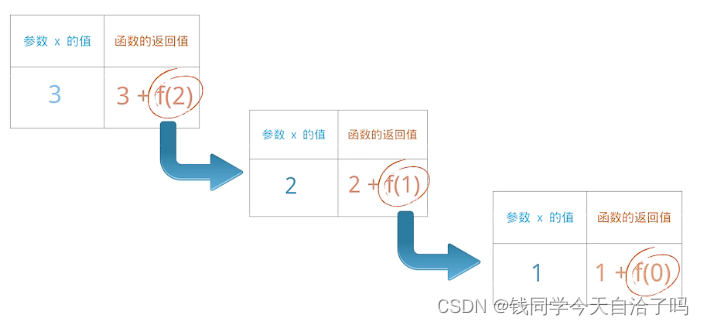
函数每次都会无条件的调用自己,为了解决这个问题,我们需要在函数中加入一个判断语句,以决定何时停止调用自己;
以参数大于0为停止条件:
def f(x):
if x > 0:
return x + f(x-1)
else:
return 0程序的运行结果是:

4、问题探讨:只递不归会怎样?
def f(x):
return x + f(x-1)
print(f(3))运行上面只递不归的函数,程序会报错;
为什么会这样呢?
在程序运行的时候,调用函数是有代价的,会占用一片叫做栈(stack)的内存空间,调用函数时,必须要放一些数据到栈里面,当函数运行结束时,这些数据会从栈里被取出;

但是,如果调用了很多函数,这些函数都不返回的话,栈就被塞满了(函数调用时往栈里面存数据,函数结束时从栈里面取出数据),数据没有地方放了,这种情况叫做栈溢出错误;对于程序运行而言,这是致命的错误,因此程序会被操作系统强行终止。

在Python中,可以人为设置递归调用的次数(深度),尽量保证程序不会崩溃。
5、小结
- 递归:函数自己调用自己
- 只递不归会导致程序崩溃
- 要在适当的时候终止递归(加if条件判断语句)
递归实例:汉诺塔问题
1、故事引入
一个印度传说。
大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上,从下往上按照大小顺序摞着64片黄金圆盘。
大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
64根柱子移动完毕之日,就是世界毁灭之时。

2、移动盘子的逻辑
假设盘子数目为n,n=3时,如果想把A中盘子全部移到C盘上
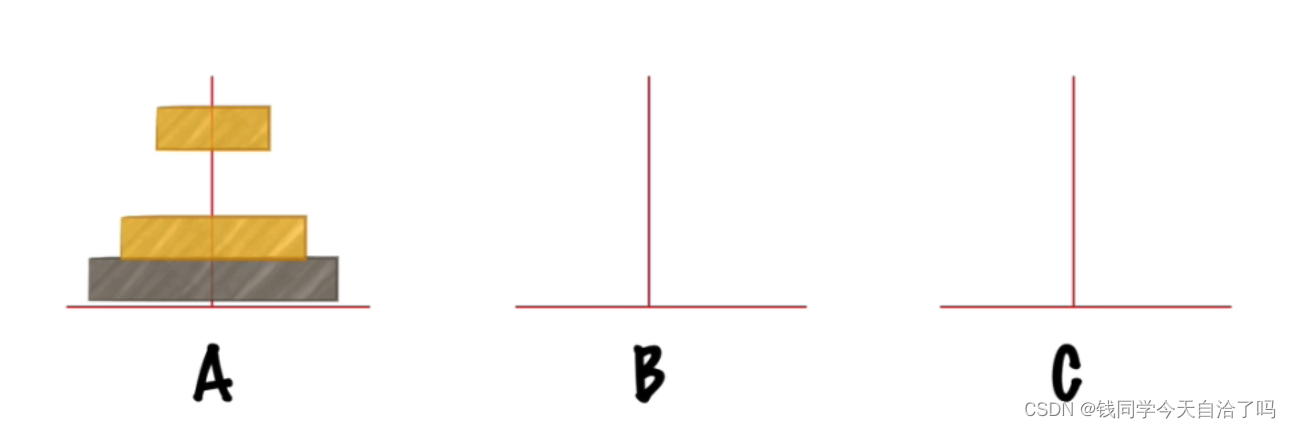
假设三个盘子分别为小、中、大,我们需要这样移动(注意要符合移动圆盘的要求):
小->C,中->B,小->B,大->C,小->A,中->C,小->C;共计七步。
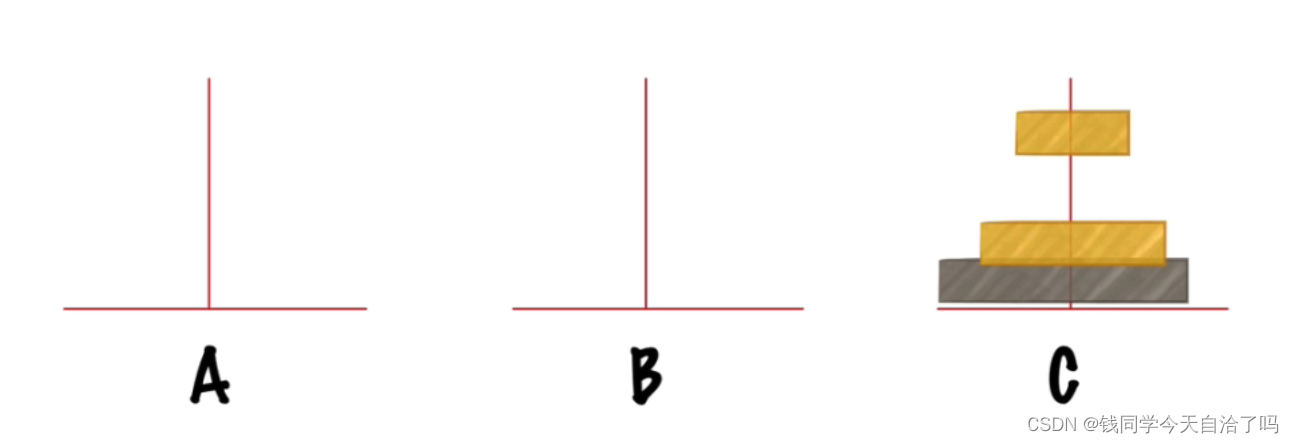
3、N个盘子的移动分析
以上述移动盘子的逻辑为例,不能推测出,移动N(N>2)个盘子时,需要下面这几步骤:
- 把n-1个圆盘从A经过C移动到B;
- 把第n个圆盘从A移动到C;
- 把n-1个小圆盘从B经过A移动到C。
4、代码实现N个盘子的移动
def hanoi(n,a,b,c):
"""
n表示圆盘数
a表示第一根柱子最上面的圆盘(圆盘的起始位置)
b表示第二根柱子最上面的圆盘(想将所有圆盘从a移动到c需要借助的柱子)
c表示第三根柱子最上面的圆盘(圆盘的目标位置)
"""
if n>0:
hanoi(n-1,a,c,b) # 步骤一:把n-1个圆盘从A经过C移动到B;
print("moving from %s to %s." % (a,c)) # 步骤二:把第n个圆盘从A移动到C;
hanoi(n-1,b,a,c) # 步骤三:把n-1个小圆盘从B经过A移动到C。
# 测试圆盘数为1、2、3时,我们的移动步骤
hanoi(1,'A','B','C')
print('------------')
hanoi(2,'A','B','C')
print('------------')
hanoi(3,'A','B','C')我们尝试打印出圆盘数分别为1、2、3时,需要移动的步骤,控制台打印结果为:
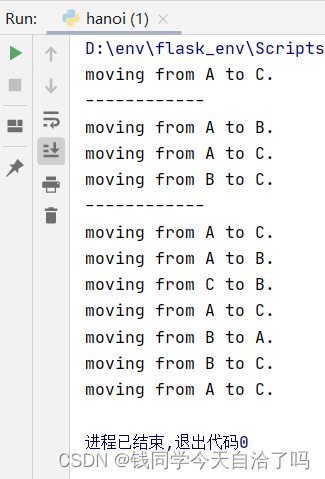
5、汉诺塔移动次数计算公式
设圆盘数为n时,移动次数为f(n);
根据N个盘子的移动分析步骤可以得知,第一步要移动f(n-1)次,第二步要移动1次,第三步要移动f(n-1)次
所以,汉诺塔移动次数计算公式为
f(n) = f(n-1) + 1 + f(n-1);
由上图打印结果可以知道,f(1)=1;f(2)=3;f(3)=7,可以带入计算公式检验一下,的确是符合的。