问题描述

给定无向连通图和m种不同的颜色，用这些颜色为图G的各个顶点着色，每个顶点有一种颜色

是否有一种着色方法？使得图G中每条边的两个顶点有不同的颜色

这个问题就是图的m可着色判定问题

色数：如果有一个图最少需要m种颜色才能使得图中每条边连接的2个顶点有着不同的颜色，称m是这个图的色数。

著名的平面图的四色猜想就是图的m可着色判定问题的特殊情形，可平面图是什么？如果一个图的所有顶点和边都可以用某一种方式画在一个平面上，并且没有任何两条边相交，就成为可平面图。

四色猜想：

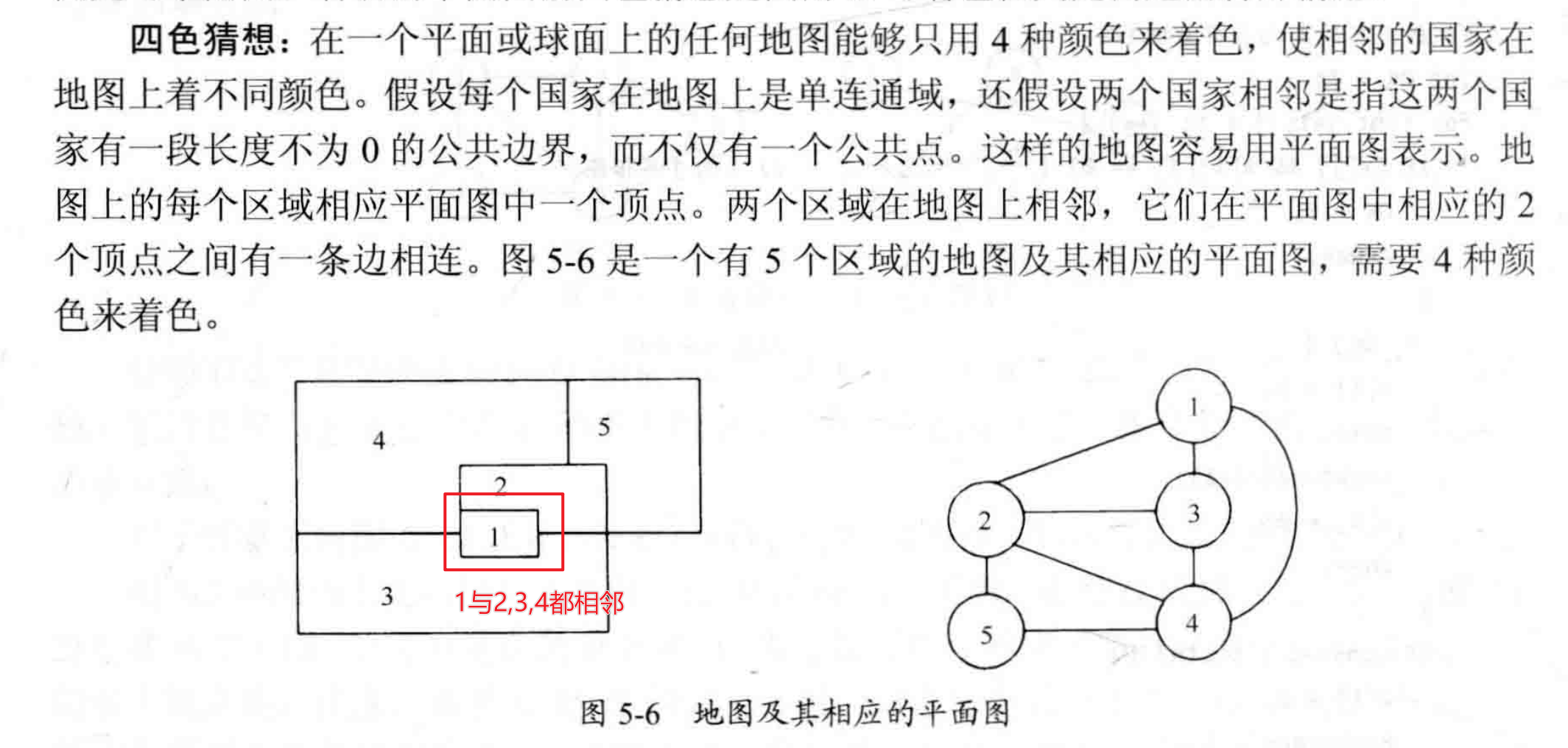
问题分析

变量声明

无向连通图G(V,E)用邻接矩阵a表示，a[ i ][ j ]=1表示i和j两个顶点之间存在一条边( i , j )，即( i , j )属于图G(V,E)的边集E。否则，a[i][j]=0。

整数1,2,3，...，m表示m种不同的颜色

顶点i的颜色用x[ i ]表示。x[ i ]就是问题的解

解空间

解空间可以表示为一颗n+1高度的完全m叉树，第i层有m个儿子，每个儿子对应X[ i ]的一种可能性

第一层就是第一个顶点，第二层第二个顶点，...，第n+1层是最后一个顶点（叶子）。每个分支结点，都有m个儿子结点。最底层有 $\text{[math]}$ 个叶子结点。

回溯逻辑

剪枝--检查什么可行性？

可行的条件是yu当前点相邻的点不能与之同色

backtrack（int i）

完整代码

#include <iostream>
#include<cstring>
#include<math.h>
using namespace std;
int n;//图一共有n个顶点
int m;//m种颜色被选择
int k;//图中有k条边
int sum=0;//图的m着色种类
int x[101];//存放当前的着色序列{...}
int a[101][101];//图的邻接矩阵
//判断给点t着色为x[t]是否可行
bool OK(int t)
{
    //可行的条件是当前点相邻的点不能与之同色
    for(int i=1;i<t;i++)
        if(a[i][t]==1&&x[i]==x[t])
            return false;
    //如果所有与之相邻的点都不与之同色
    return true;
}
void backtrack(int i)
{
    if(i>n){//i>n说明找到了一个可行的涂色方案
        sum++;//涂色方案数++
        //这里可以选择性的输出解向量
        for(int k=1;k<=n;k++)
            cout<<x[i]<<" ";
        cout<<endl;
        return ;
    }
    //还没有到叶子节点，需要给当前节点可行的涂色
    else{
        for(int k=1;k<=m;k++){    //子树是一个m叉树
            x[i]=k;//给第i个顶点着第k种颜色
            if(OK(i))//剪枝
                backtrack(i+1);
            x[i]=0;//如果给第i个顶点着第k种颜色不可行
            //不涂色，便于后续涂色
        }
    }
    return ;//如果当前节点所有颜色都不可行，结束对子树的遍历，返回
}
int main()
{
    cin>>n>>k>>m;//输入定点数，边数，着色种类数
    int x,y;
    memset(a,0,sizeof(a));//给邻接矩阵赋初值
    for(int i=1;i<=k;i++){
        cin>>x>>y;
        a[x][y]=a[y][x]=1;//生成邻接矩阵
    }
    backtrack(1);
    cout<<"sum= "<<sum;//输出最大可行的着色方案数，sum初始值为0
    return 0;
}

测试用例

输入

输入定点数，边数，着色种类数

5 8 4

1 2

1 3

1 4

2 3

2 4

2 5

3 4

4 5