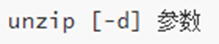
1.概述：

在使用相机拍照片时，大多数人会考虑拍的好不好看，关注相机中物体坐标的并不多，但是对于地信学科来说，如果能从照片中获取物体的真实位置，对地理信息获取大有帮助，在这里面，十分关键的一步就是相机标定。

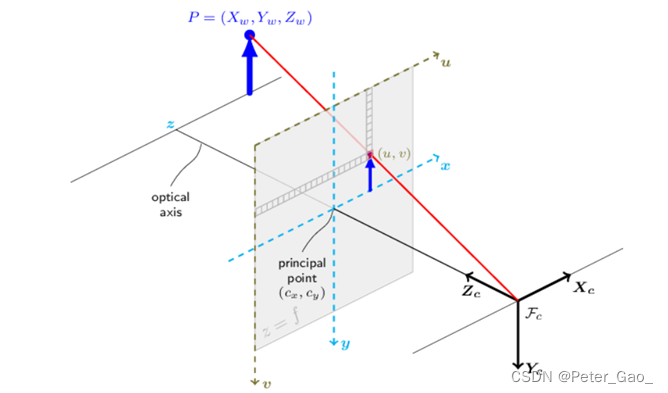
相机标定的基本原理也是相对简单的，看官网中的一个示意图，很容易发现，物点P(Xw,Yw,Zw)，像点(u,v)和相机点三点在同一条线上（红线），如果知道多对物点和像点，画出他们的连线，找到的焦点就是相机的位置，同时还可以根据这些线的走向解算相机的旋转角，旋转角和坐标偏移共同构成了相机的外参。（实际上，这里的像点并不是照片中物体的坐标，而是相机中感光片上的坐标，他们的转化需要一定的几何变化）

2.基本假设

影响上面相机外参精度的变量有很多，例如镜头畸变，像主点跟感光片的相对位置等等，这些可以归纳为相机的内参。

在此仅使用OpenCV-Python中的函数做一个小实验，拍摄工具是手机，所以也不方便找到这些参数，因此不考虑内参的影响，假设相机内参是完美的，即没有畸变和偏移。

所以它的内参矩阵可以假设为下面的样子，27是我手机拍照时显示的焦距，单位mm，8.17是用宽度的像素个数除以照片宽度得到的，也就是1mm有多少像素：

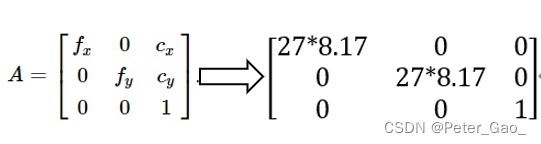
假设没有畸变，因此畸变参数全部设置为0

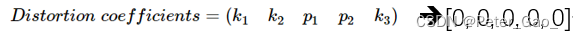
参考了这个文章;

https://blog.csdn.net/weixin_44671418/article/details/109386911

3.坐标获取

基于上面的假设，问题就简单多了，需要的数据只有物点坐标，像点坐标，在这里拍摄了一个照片，用来提供上面的数据，A4纸上画的是X轴和Y轴，电脑屏幕的棋盘作为Z轴刻度，电脑屏幕棋盘的第一条线距离桌面8.5cm。

下面的代码可帮助获取屏幕坐标，在输入真实坐标后，保存这些坐标

import numpy as np
import cv2 as cv
import glob
#定义两个列表，realcoo存储真实坐标，imacoo存储相片坐标
imacoo=[]
realcoo=[]
#OpenCV点击相片的事件相应函数，左键双击提示输入三维坐标，右键双击保存输入的点为numpy的一种文件格式，便于后续使用
def GetCoordinate(event,x,y,flags,param):
    #event判断事件类型，右键双击保存为cooimfoText.npz文件
    if event == cv.EVENT_RBUTTONDBLCLK:
        np.savez('cooimfoText.npz', imacoo=imacoo, realcoo=realcoo)
    #如果是左键双击，就键入物体的真实坐标
    if event == cv.EVENT_LBUTTONDBLCLK:
        print(x,y)
        strcoo = input("请输入三维坐标，以逗号隔开")
        coo = strcoo.split(',')
        realcoo.append((float(coo[0]), float(coo[1]), float(coo[2])))
        imacoo.append((x,y))
#打开图像
img = cv.imread("IMG_20221028_151422.jpg")
width,height=img.shape[:2]
#由于手机分辨率太高了，电脑屏幕显示不下，所以缩放一下
imgresize = cv.resize(img,(int(0.2*height), int(0.2*width)), interpolation = cv.INTER_CUBIC)
#窗口命名
cv.namedWindow('room')
#事件绑定
cv.setMouseCallback('room',GetCoordinate)
#打开图像，开始采集点坐标
cv.imshow('room',imgresize)
key=cv.waitKey(0)

4. 外参解算

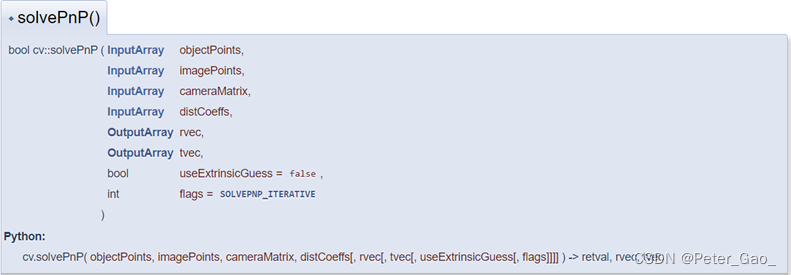
解算主要用到了OpenCV的这个函数solvePnP()，看下图它的参数，第一个就是上面的物点坐标，第二个是像点坐标，第三个是相机参数A(在上面已经做了假设)，第四个是畸变参数(假设为[0,0,0,0,0])，它的返回值就是rvec：相机旋转参数，tvec相机平移参数

使用下面的代码完成解算过程

import numpy as np
import cv2 as cv
 
#根据假设，定义的相机内部参数和畸变参数
M = np.asarray([[27 * 8.17, 0, 0], [0, 27 * 8.17, 0], [0, 0, 1]], dtype=float)
C = np.asarray([0, 0, 0, 0, 0], dtype=float)
#打开刚获取到的坐标文件
with np.load('cooimfoText.npz') as X:
    imacoo = X['imacoo']
    realcoo = X['realcoo']
    #屏幕坐标转迪卡尔坐标
    for i in range(0,len(imacoo)):
        imacoo[i][1]=793-imacoo[i][1]
    #转化为浮点型
    realcoo = realcoo.astype(np.float32)
    imacoo = imacoo.astype(np.float32)
    #解算相机外参
    retval, rvec, tvec = cv.solvePnP(realcoo, imacoo,M, C)
    #打印结果
    print("解算结果：",retval)
    print("旋转角度：",rvec)
    print("偏移距离：",tvec)

输出结果为：