前言

本节内容我们主要介绍一下在jenkins中如何集成sonar qube代码质量检查工具，sonar qube可以在流水化项目集成部署前对我们的代码质量检查。开始本节内容前我们需要先搭建好sonar qube服务，关于sonar qube服务的搭建可参考作者往期博客内容，本节内容不在涉及。

（六）centos7案例实战——sonarQube安装及springboot项目集成sonarQube完成代码质量检查_北溟溟的博客-CSDN博客

正文

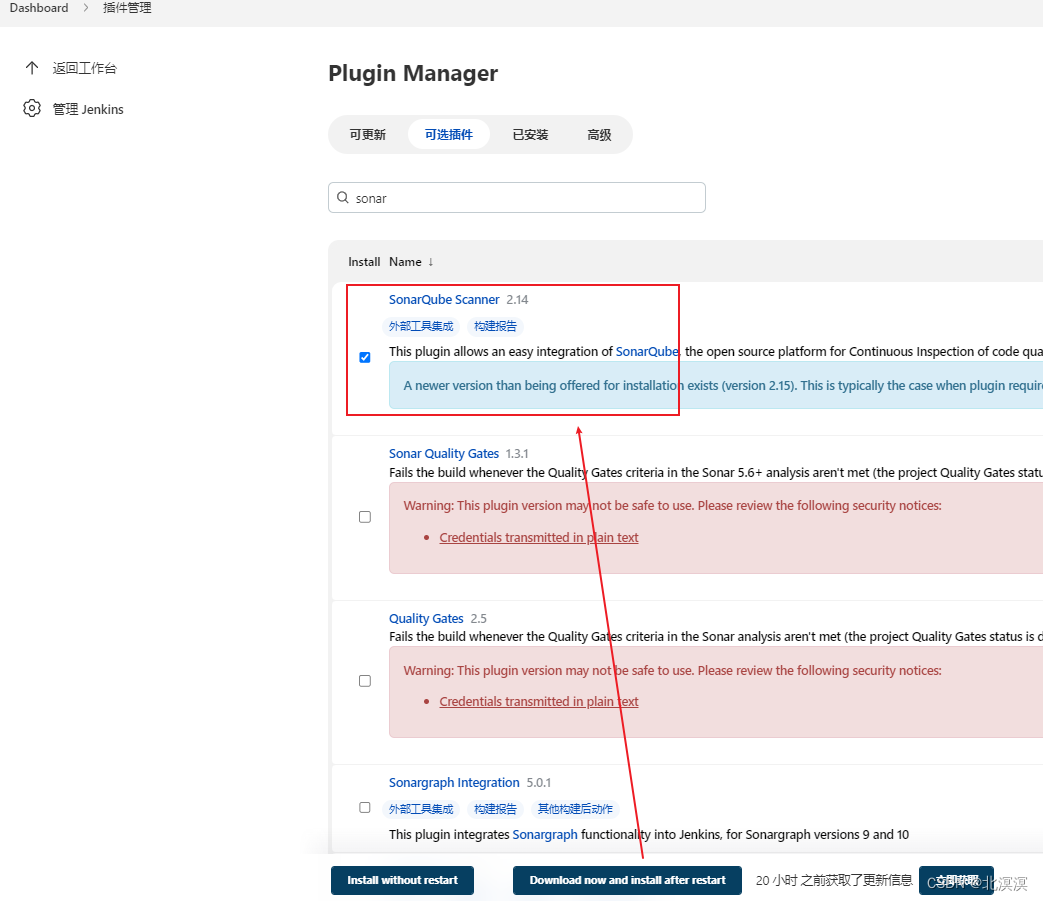
①点击系统管理->插件管理

②安装sonar qube组件

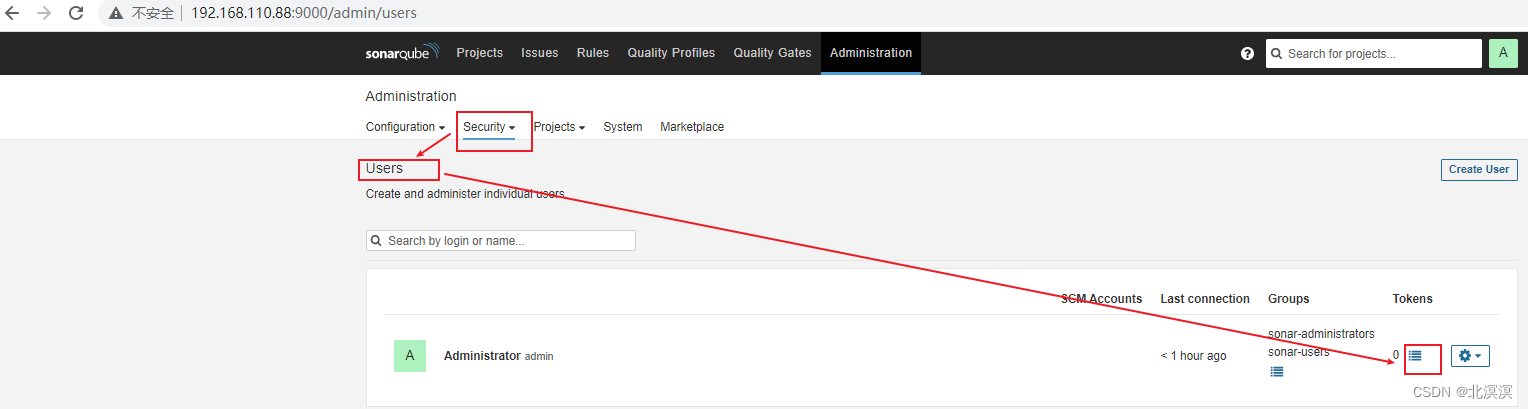
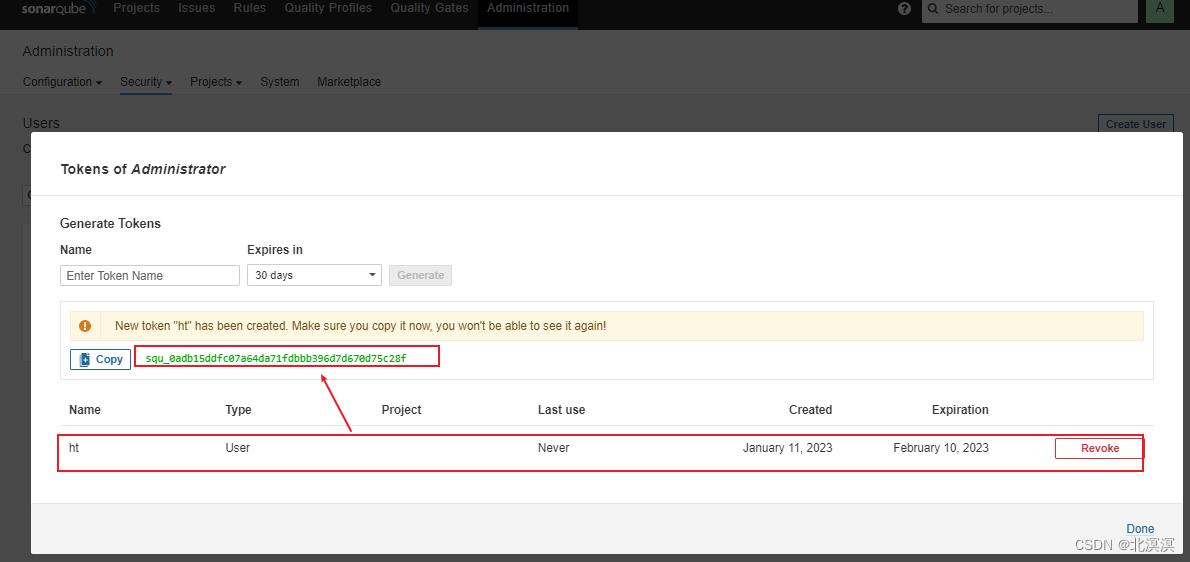
 ③登录sonar qube服务创建一个用于授权jenkins访问的token

 ④点击系统管理，全局凭据，添加SonarQube凭证

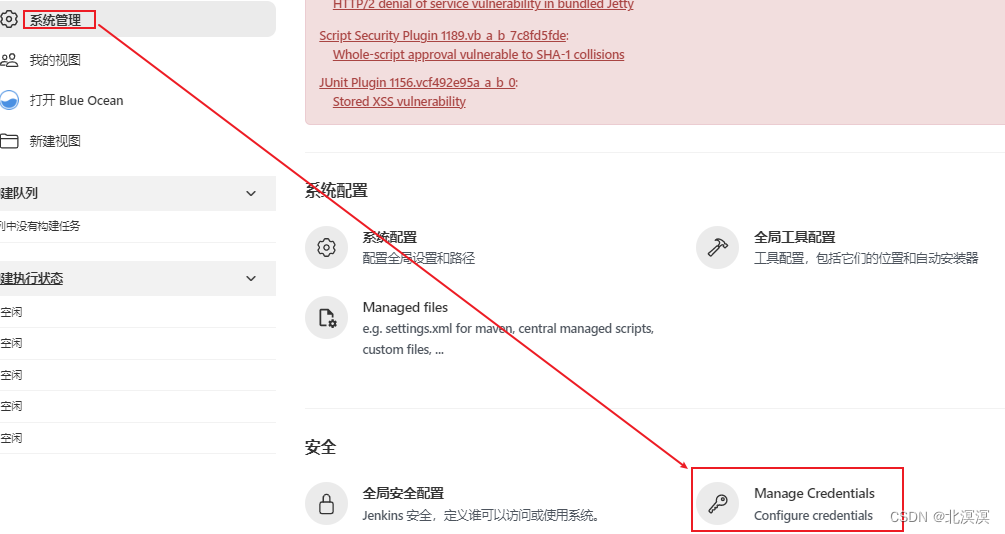
 ⑤创建sonar qube全局账号

 ⑥点击保存，sonar qube全局账号配置完成

⑦ 点击系统管理->系统配置，配置sonar qube服务并保存

 ⑧点击系统管理->全局工具配置，安装SonarQube Scanner扫描

⑨进入sonar qube服务，打开审查结果上传到SCM功能 

⑩篇幅有限，关于流水化项目集成sonar qube请关注我的后续文章内容，这里只是展示下效果

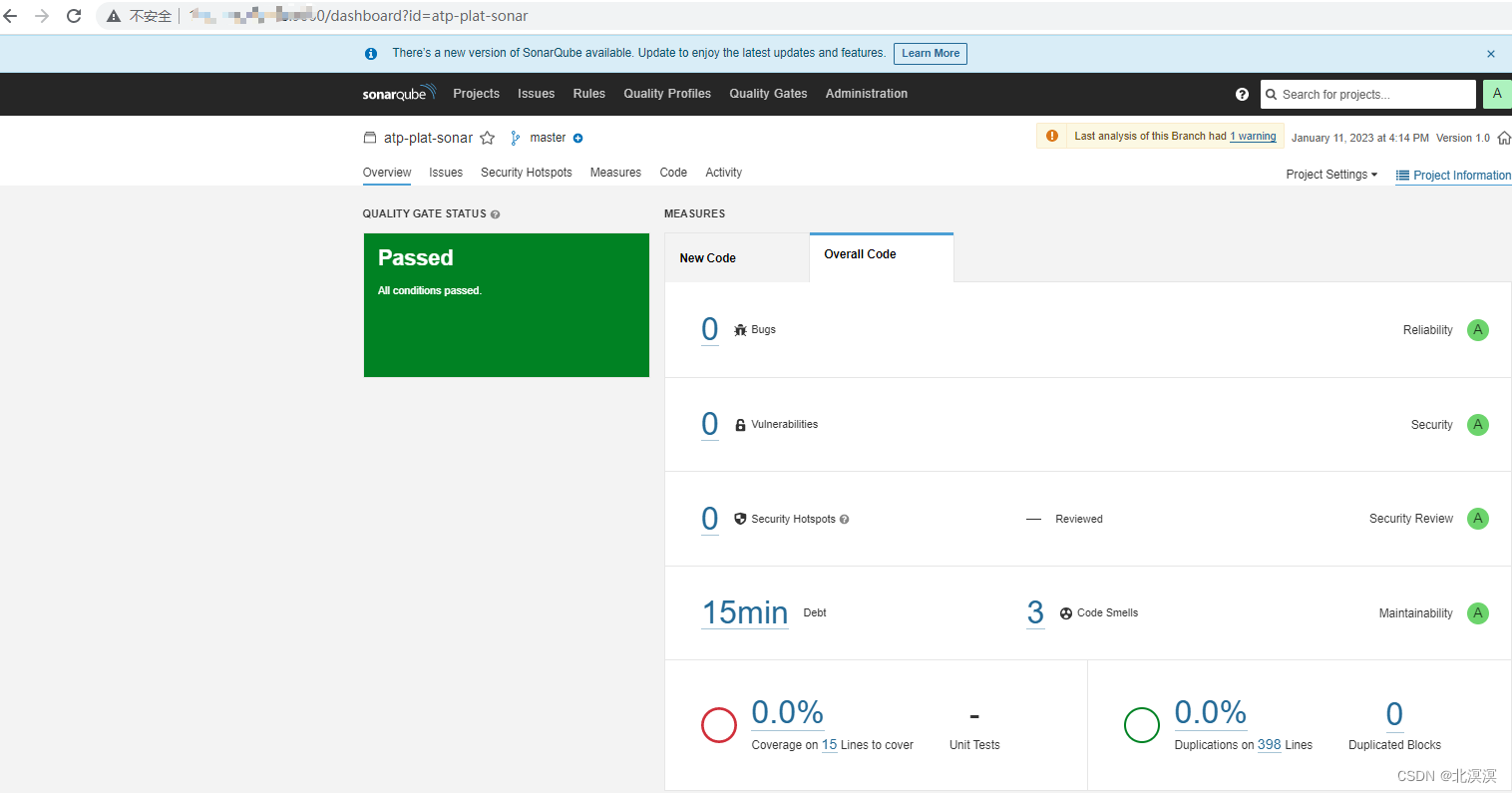
结语

至此，关于jenkins的全局工具配置之sonar qube环境安装及配置到这里就结束了，后期还会推出其它devops的相关内容，感谢关注、点赞、收藏支持，我们下期见。。。