01.任何一个无向连通图的最小生成树( )。
A.有一棵或多棵 B.只有一棵
C.一定有多棵 D.可能不存在
02.用Prim算法和Kruskal算法构造图的最小生成树,所得到的最小生成树()。
A.相同 B.不相同
C.可能相同,可能不同 D.无法比较
03.以下叙述中,正确的是( )。
A.只要无向连通图中没有权值相同的边,则其最小生成树唯一
B.只要无向图中有权值相同的边,则其最小生成树一定不唯一
C.从n个顶点的连通图中选取n-1条权值最小的边,即可构成最小生成树
D.设连通图G含有n个顶点,则含有n个顶点、n-1条边的子图一定是G的生成树
04.设有n个顶点的无向连通图的最小生成树不唯一,则下列说法中正确的是( )。
A.图的边数一定大于n- 1
B.图的权值最小的边一定有多条
C.图的最小生成树的代价不一定相等
D.图的各条边的权值不相等
05.用Prim算法求一个带权连通图的最小生成树,在算法执行的某个时刻,已选取的顶点
集合U={1,2,3},已选取的边集合TE={(1,2),(2,3)},要选取下一条权值最小的边,应当从( )组中选取。
A. {(1,4),(3,4),(3,5),(2,5)}
B.{(3,4),(3,5), (4,5), (1,4)}
C. {(1,2),(2,3),(3,5)}
D. {(4,5), (1,3),(3,5)}
06.用Kruskal算法求一个带权连通图的最小生成树,在算法执行的某个时刻,已选取的边
集合TE={(1,2),(2,3),(3,5)},要选取下一条权值最小的边,不可能选取的边是( ).
A.(3,6)
B. (2,4)
C. (1,3)
D. (1,4)
07.下列关于图的最短路径的相关叙述中,正确的是( ).
A.最短路径一定是简单路径
B.Dijkstra算法不适合求有回路的带权图的最短路径
C.Dijkstra算法不适合求任意两个顶点的最短路径
D.Floyd算法求两个顶点的最短路径时,pathk-1一定是pathk的子集
08.下列关于图的最短路径的相关叙述中,正确的是( )。
Ⅰ Dijkstra算法求单源最短路径不允许边的权为负
Ⅱ.Dijkstra算法求每对顶点间的最短路径的时间复杂度是O(n2)
Ⅲ. Floyd算法求每对顶点间的最短路径允许边的权为负,但不允许含有负边的回路
A.I、Ⅱ和Ⅲ B.仅I C.I和Ⅲ D.II和Ⅲ
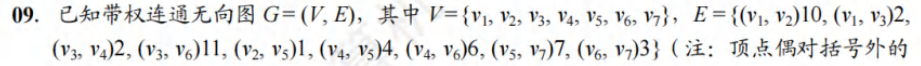

10. 用Dijkstra算法求一个带权有向图的从顶点0出发的最短路径,在算法执行的某个时刻,已求得的最短路径的顶点集合S= {0,2,3,4},下一个选取的目标顶点是顶点1,则可能修改的最短路径是()。
A.从顶点0到顶点3的最短路径
B.从顶点0到顶点2的最短路径
C.从顶点2到顶点4的最短路径
D.从顶点0到顶点1的最短路径
11.下面的( )方法可以判断出一个有向图是否有环(回路)。
Ⅰ深度优先遍历 Ⅱ.拓扑排序 Ⅲ.求最短路径 IV.求关键路径
A.I、II、IV B.I、Ⅲ、IV C.I、II、Ⅲ D.全部可以
12.在有向图G的拓扑序列中,若顶点v在顶点v之前,则不可能出现的情形是( )。
A.G中有弧<vi,vj>
B.G中有一条从vi到vj的路径
C.G中没有弧<vi,vj>
D.G中有一条从vj到vi的路径
13.下列关于拓扑排序的说法中,错误的是()。
Ⅰ若某有向图存在环路,则该有向图一定不存在拓扑排序
Ⅱ.在拓扑排序算法中为暂存入度为零的顶点,可以使用栈,也可以使用队列
Ⅲ、若有向图的拓扑有序序列唯一,则图中每个顶点的入度和出度最多为1
IV.若有向图的拓扑有序序列唯一,则图中入度为0和出度为0的顶点都仅有1个
A.I、Ⅲ、IV B.Ⅲ、IV C.II、IV D.Ⅲ
14.下列关于拓扑排序的说法中,正确的是().
Ⅰ强连通图不能进行拓扑排序
II.在一个有向图的拓扑序列中,若顶点a在顶点b之前,则图中必有一条弧<a, b>A.仅I
B.仅П
C.I和I
D,都不正确
15.若一个有向图的顶点不能排成一个拓扑序列,则判定该有向图( ).
A.含有多个出度为0的顶点
B.是个强连通图
C.含有多个入度为0的顶点
D.含有顶点数大于1的强连通分量
16.下图所示有向图的所有拓扑序列共有()个。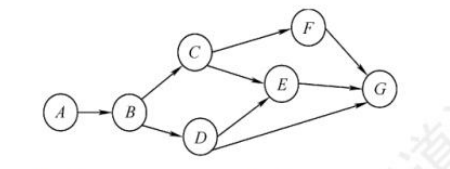
A.4
B.6
C.5
D.7

18.下列哪种图的邻接矩阵是对称矩阵?()
A.有向网
B.无向图
C.AOV网
D.AOE网
19.若一个有向图具有有序的拓扑排序序列,则它的邻接矩阵必定为()。
A.对称
B.稀疏
C.三角
D.一般
20.用DFS算法遍历一个无环有向图,并在 DFS算法退栈返回时输出相应的顶点,则输出的顶点序列是()。
A.逆拓扑有序 B.拓扑有序 C.无序的 D.无法确定
21.下列关于图的说法中,正确的是().
Ⅰ有向图中顶点V的度等于其邻接矩阵中第V行中1的个数
Ⅱ.无向图的邻接矩阵一定是对称矩阵,有向图的邻接矩阵一定是非对称矩阵
Ⅲ.在带权图G的最小生成树G中,某条边的权值可能会超过未选边的权值
IV.若有向无环图的拓扑序列唯一,则可以唯一确定该图
A. I、II和Ⅲ B.Ⅲ和IV C.Ⅲ D.IV
22.下图所示的AOE网中,关键路径长度为()。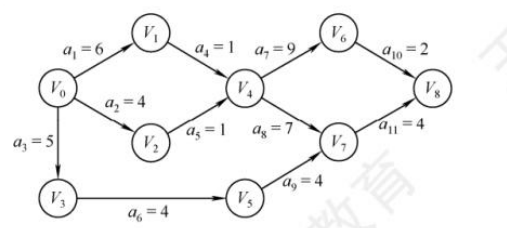
A. 16 B. 17 C. 18 D. 19

A.19 B.20 C. 21 D.22
24.下面关于求关键路径的说法中,不正确的是( )。
A.求关键路径是以拓扑排序为基础的
B.一个事件的最早发生时间与以该事件为始的弧的活动的最早开始时间相同
C.一个事件的最迟发生时间是以该事件为尾的弧的活动的最迟开始时间与该活动的持
续时间的差
D.任何一个活动的持续时间的改变可能会影响关键路径的改变
25.下列关于关键路径的说法中,正确的是()
Ⅰ改变网上某一关键路径上的任意一个关键活动后,必将产生不同的关键路径
Ⅱ.在AOE图中,关键路径上活动的时间延长多少,整个工期也就随之延长多少
Ⅲ.缩短关键路径上任意一个关键活动的持续时间可缩短关键路径长度
IV.缩短所有关键路径上共有的任意一个关键活动的持续时间可缩短关键路径长度
V.缩短多条关键路径上共有的任意一个关键活动的持续时间可缩短关键路径长度
A.Ⅱ和V
B.Ⅰ、Ⅱ和IV
C.Ⅱ和IV
D.Ⅰ和IV
26.在求AOE网的关键路径时,若该有向图用邻接矩阵表示且第i列值全为o,则( )。
A.若关键路径存在,第i个顶点一定是起点
B.若关键路径存在,第i个顶点一定是终点
C.关键路径不存在
D.该有向图对应的无向图存在多个连通分量
27.【2010统考真题】对下图进行拓扑排序,可得不同拓扑序列的个数是( )。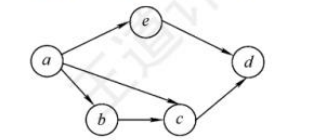
A.4
B.3
C.2
D.1
28.【2012统考真题】下列关于最小生成树的叙述中,正确的是()。
Ⅰ.最小生成树的代价唯一
Ⅱ.所有权值最小的边一定会出现在所有的最小生成树中
Ⅲ.使用Prim算法从不同顶点开始得到的最小生成树一定相同
IV.使用Prim算法和Kruskal算法得到的最小生成树总不相同
A.仅Ⅰ
B.Ⅰ、Ⅱ和IV
C.Ⅱ和IV
D.Ⅰ和IV
29.【2012统考真题】对下图所示的有向带权图,若采用Dijkstra算法求从源点α到其他各顶点的最短路径,则得到的第一条最短路径的目标顶点是b,第二条最短路径的目标顶点是c,后续得到的其余各最短路径的目标顶点依次是()。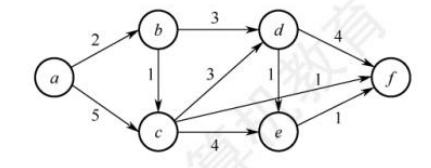
A. d, e,f
B. e, d,f
C. f, d, e
D. f, e, d
30.【2012统考真题】若用邻接矩阵存储有向图,矩阵中主对角线以下的元素均为零,则关于该图拓扑序列的结论是().
A.存在,且唯一 B.存在,且不唯一
C.存在,可能不唯一 D.无法确定是否存在
31.【2013统考真题】下列AOE网表示一项包含8个活动的工程。通过同时加快若干活动的进度可缩短整个工程的工期。在下列选项中,加快其进度就可缩短工程工期的是()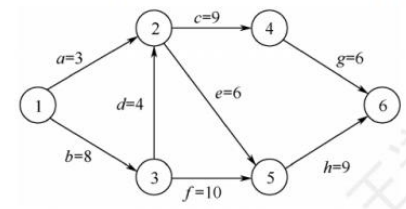
A.c和e B.d和c C.f和d D.f和h
32.【2014统考真题】对下图所示的有向图进行拓扑排序,得到的拓扑序列可能是()。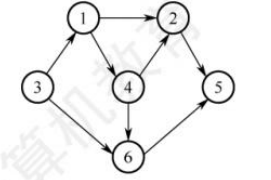
A. 3,1,2,4,5,6 B. 3,1,2,4,6,5 C. 3,1,4,2,5,6 D.3,1,4,2,6,5
33.【2015统考真题】求下面的带权图的最小(代价)生成树时,可能是Kruskal算法第2次选中但不是Prim算法(从V开始)第2次选中的边是()。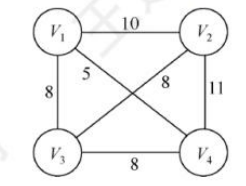
A.(V1, V3) B. (V1, V4) C. (V2, V3) D. (V3, V4)
34.【2011统考真题】下列关于图的叙述中,正确的是( )。
Ⅰ.回路是简单路径
Ⅱ.存储稀疏图,用邻接矩阵比邻接表更省空间
Ⅲ.若有向图中存在拓扑序列,则该图不存在回路
A.仅Ⅱ
B.仅Ⅰ、Ⅱ
C.仅Ⅲ
D.仅Ⅰ、Ⅲ
35.【2016统考真题】使用Dijkstra算法求下图中从顶点1到其他各顶点的最短路径,依次
得到的各最短路径的目标顶点是()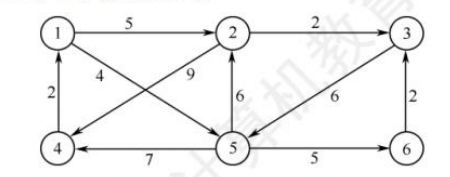
A. 5,2,3,4,6
B. 5,2,3,6,4
C. 5,2,4,3,6
D.5,2,6,3,4
36.【2016统考真题】若对n个顶点、e条弧的有向图采用邻接表存储,则拓扑排序算法的时间复杂度是()。
A. O(n)
B.O(n+e)
C. O(n2)
D. O(ne)
37.【2018统考真题】下列选项中,不是如下有向图的拓扑序列的是().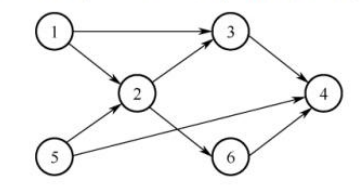
A.1,5,2,3,6,4
B. 5,1,2,6,3,4
C. 5,1,2,3,6,4
D.5,2,1,6,3,4
38.【2019统考真题】下图所示的AOE网表示一项包含8个活动的工程。活动d的最早开始时间和最迟开始时间分别是( ).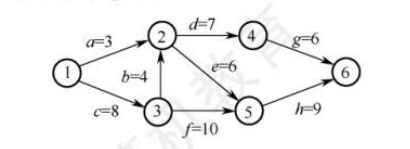
A.3和7 B.12和12 C.12和 14 D.15和15
39.【2019统考真题】用有向无环图描述表达式(x+y)(x+y)/x),需要的顶点个数至少是
( ).
A.5 B.6 C. 8 D.9
40.【2020统考真题】已知无向图G如下所示,使用Kruskal算法求图G的最小生成树,加到最小生成树中的边依次是( ).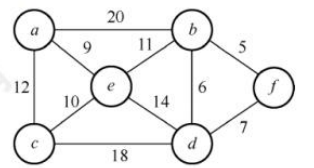
A. (b,f) (b, d ),(a, e),(c, e), (b, e) B. (b,f ), (b, d), (b, e),(a, e), (c, e)
C. (a, e), (b,e), (c, e), (b, d ),(b,f ) D. (a,e),(c,e), (b,e),(b,f), (b,d )
41. 【2020统考真题】修改递归方式实现的图的深度优先搜索(DFS)算法,将输出(访问)顶点信息的语句移到退出递归前(即执行输出语句后立刻退出递归)。采用修改后的算法遍历有向无环图G,若输出结果中包含G中的全部顶点,则输出的顶点序列是G的( )。
A.拓扑有序序列 B.逆拓扑有序序列
C.广度优先搜索序列 D.深度优先搜索序列
42.【2020统考真题】若使用AOE网估算工程进度,则下列叙述中正确的是()。
A.关键路径是从源点到汇点边数最多的一条路径
B.关键路径是从源点到汇点路径长度最长的路径
C.增加任意一个关键活动的时间不会延长工程的工期
D.缩短任意一个关键活动的时间将会缩短工程的工期
43.【2021统考真题】给定如下有向图,该图的拓扑有序序列的个数是()。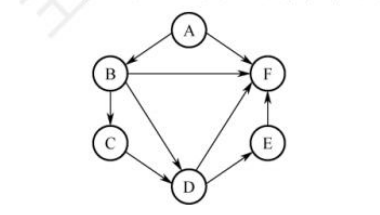
A.1 B.2 C.3 D.4
44.【2021统考真题】使用Dijkstra算法求下图中从顶点1到其余各顶点的最短路径,将当前找到的从顶点1到顶点2,3,4,5的最短路径长度保存在数组dist 中,求出第二条最短路径后,dist中的内容更新为()。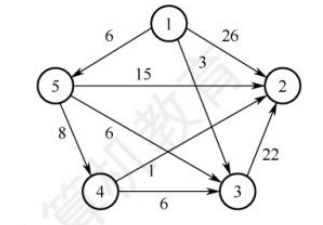
A. 26,3,14,6 B.25,3,14,6 C.21,3, 14,6 D. 15,3,14,6
45.【2022统考真题】下图是一个有10个活动的AOE网,时间余量最大的活动是()。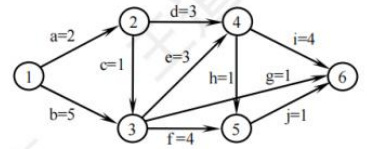
A.c B.g C. h D. j
46.【2023统考真题】已知无向连通图G中各边的权值均为1。在下列算法中,一定能够求出图G中从某顶点到其余各顶点最短路径的是( )。
ⅠPrim算法 Ⅱ.Kruskal算法 Ⅲ.图的广度优先搜索算法
A.仅I B.仅Ⅲ C.仅Ⅰ、Ⅱ D.Ⅰ、Ⅱ、IⅢ