Problem: 84. 柱状图中最大的矩形

题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

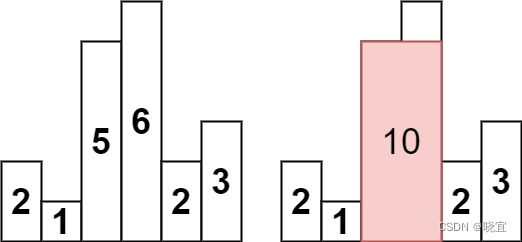
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

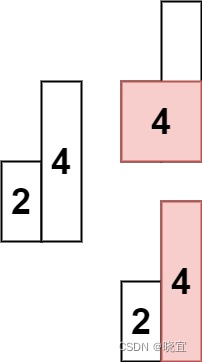
输入： heights = [2,4]
输出： 4

思路

对于一根柱子x，其高为h.假如我们知道了他左边的第一根小于他的柱子的位置l和邮编第一个小于的高度的柱子r，那么我们很容易求得他的最大面积为：$s=(r-l-1)\ast h$

根据这一性质，我们采用单调栈的方法，在栈中保留第一个比当前元素小的元素的索引，所有大于当前元素的索引都将被弹出；如果栈不为空，说明存在这样一个索引，其对应的元素值小于当前元素，我们记录他。

我们分别从左往右和从右往左计算两遍，最后得出答案

复杂度

时间复杂度:

$O(n)$

空间复杂度:

$O(n)$

Code

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        left = [-1] * n
        st = []
        for i,x in enumerate(heights):
            while st and heights[st[-1]] >= x:
                st.pop()
            if st:
                left[i] = st[-1]
            st.append(i)

        right = [n] * n
        st.clear()
        for i in range(n-1,-1,-1):
            x = heights[i]
            while st and heights[st[-1]] >= x:
                st.pop()
            if st:
                right[i] = st[-1]

            st.append(i)
        
        ans = 0
        for h,l,r in zip(heights,left,right):
            ans = max(ans,h*(r-l-1))
        return ans