02-K近邻算法

机器学习其实有一个很朴实的想法: 预测 $x$ 的值，那就在训练集 $X$ 中找到与 $x$ 相似的样本，再把与x相似的这些样本的值加权作为预测值
那么我们如何度量样本之间的相似性？又该如何加权呢？
在k近邻中，我们一般采用欧式距离来寻找距离待测样本x最近的k个样本点，然后根据这k个样本点的信息推测出待测样本的目标属性值。

KNN概述

KNN（K-Nearest Neighbor，K 近邻）算法是一种与众不同的机器学习算法，它只是机械地记住所有的数据，本质上并没有拟合这一操作，所以它也被称为一种懒惰的机器学习算法。

KNN算法是基于实例的学习属于非参数模型。基于实例学习的模型以记忆训练集为特征，懒惰学习是基于实例学习的一种特殊情况，这与它在学习过程中付出零代价有关。

KNN是懒惰学习的典型例子。所谓的懒惰，并不是说它看上去很简单，而在于它不是从训练数据中学习判别函数，而是靠记忆训练过的数据集来完成任务。

KNN 历史悠久，早已为人所知。不过，该算法虽然简单，却可以学习复杂的边界。

KNN既可用于分类，也可用于回归。KNN算法在训练时机械地记住所有的训练数据。相较于其他算法要经历“根据训练数据计算最佳参数”的训练阶段和“使用计算出的学习参数进行预测”的预测阶段，KNN在训练阶段不进行任何计算，只是简单的存储训练数据，直到进入预测阶段之后才进行具体的计算。

在对未知数据进行分类时，KNN将计算未知数据与每一个训练数据的距离，通过多数表决找到最邻近的 $k$ 个点，然后进行分类。

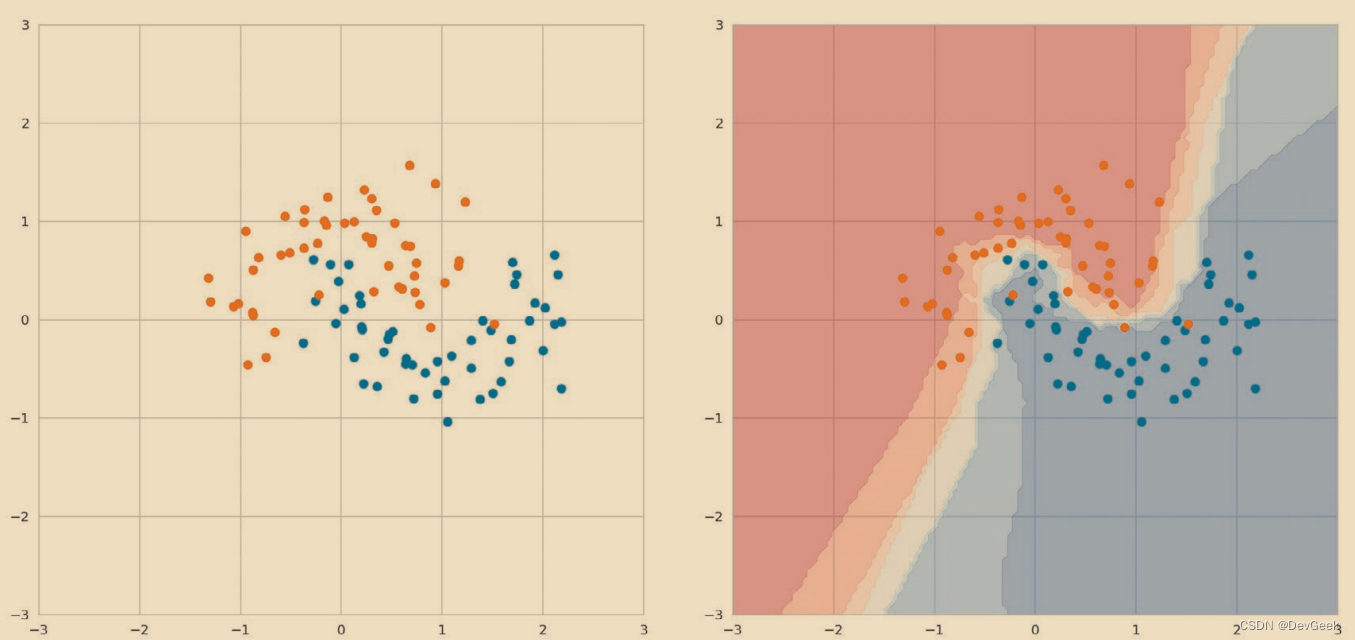
KNN虽然是一种简单的算法，但也适用于具有复杂边界的数据。下图是将KNN应用于具有复杂边界的数据而得到的结果。

KNN

优点：精度高、对异常值不敏感、无数据输入设定
缺点：计算复杂度高、空间复杂度高
使用数据范围：数值型和标称型

标称属性(nominal attribute)意味着’与名称相关’，它的值是一些符号或事物的名称。每个值代表某种类别，编码或状态，因此标称属性又被看作是分类的(categorical)。这些值不必具有有意义的序。在计算机科学中，这些值也被看做是枚举的(enumeration)。在标称属性上，数学运算是没有意义的。我们在将数据输入到模型前通常会对标称数据进行适当的编码

KNN算法原理

K近邻(K-nearst neighbors；KNN)是一种基本的机器学习算法，所谓k近邻，就是k个最近的邻居的意思，说的是每个样本都可以用它最接近的 k 个邻居来计算出自己与不同类别的数据的相似度。比如：判断一个人的人品，只需要观察与他来往最密切的几个人的人品好坏就可以得出，即“近朱者赤，近墨者黑”；KNN算法既可以应用于分类应用中，也可以应用在回归应用中。

KNN算法的工作原理：存在一个样本数据集合，也称训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据域所属类别的对应关系。KNN算法拟合的过程就是对这些训练数据进行存储，当我们向学习器输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似的数据（最近邻）的分类标签一般来说，我们只选择训练数据集中前k个最相似的数据，这就是k-近邻算法中k的出处，通常k是不大于20的奇数。最后，选择k个最相似数据中出现次数最多的分类，作为新数据的分类。

KNN在做回归和分类的主要区别在于最后做预测的时候的决策方式不同。 KNN在分类预测时，一般采用多数表决法；而在做回归预测时，一般采用平均值法。

我们在使用KNN算法时多采用加权多数表决法和加权平均值法，我们会将k个邻近样本的权重总和归一化为1（除以总权重本身就归一化为1），并且我们也把每个样本的权重都除以总权重来得到单个样本所对应的权重。

从训练集合中获取k个离待预测样本距离最近的样本数据
根据获取得到的K个样本数据来预测当前待预测样本的目标属性值。

最近邻点k的数量是一个超参数。在二元分类时，通常取k为奇数，这样多数表决才能决定结果是其中的哪一个

在这里插入图片描述

一个案例了解KNN

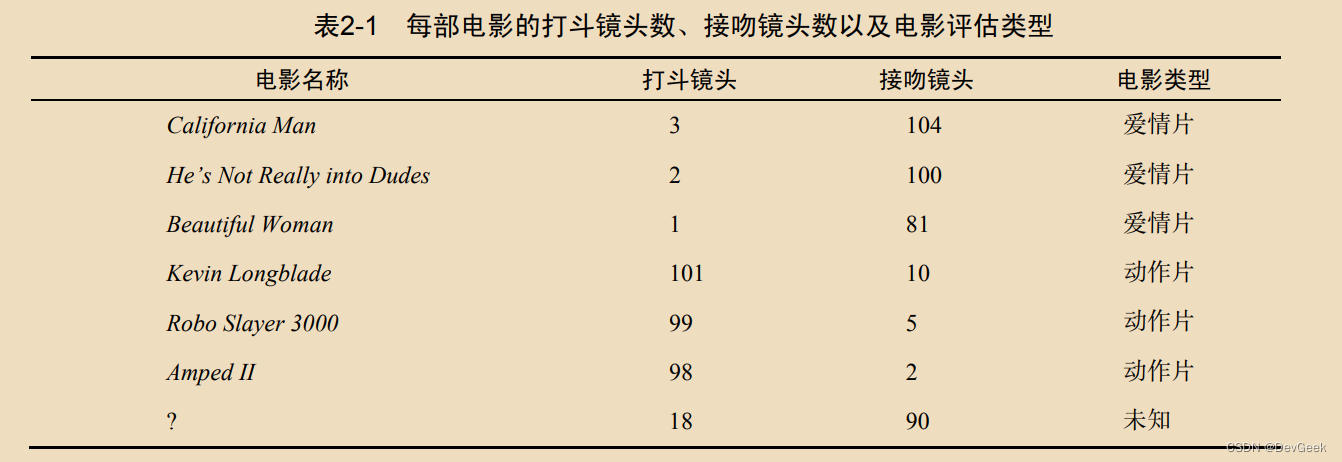
在这里插入图片描述

我们标记的电影的类型: 爱情片、动作片
每个电影有两种特征属性: 打斗镜头，接吻镜头
任务: 预测一个新电影的电影类型
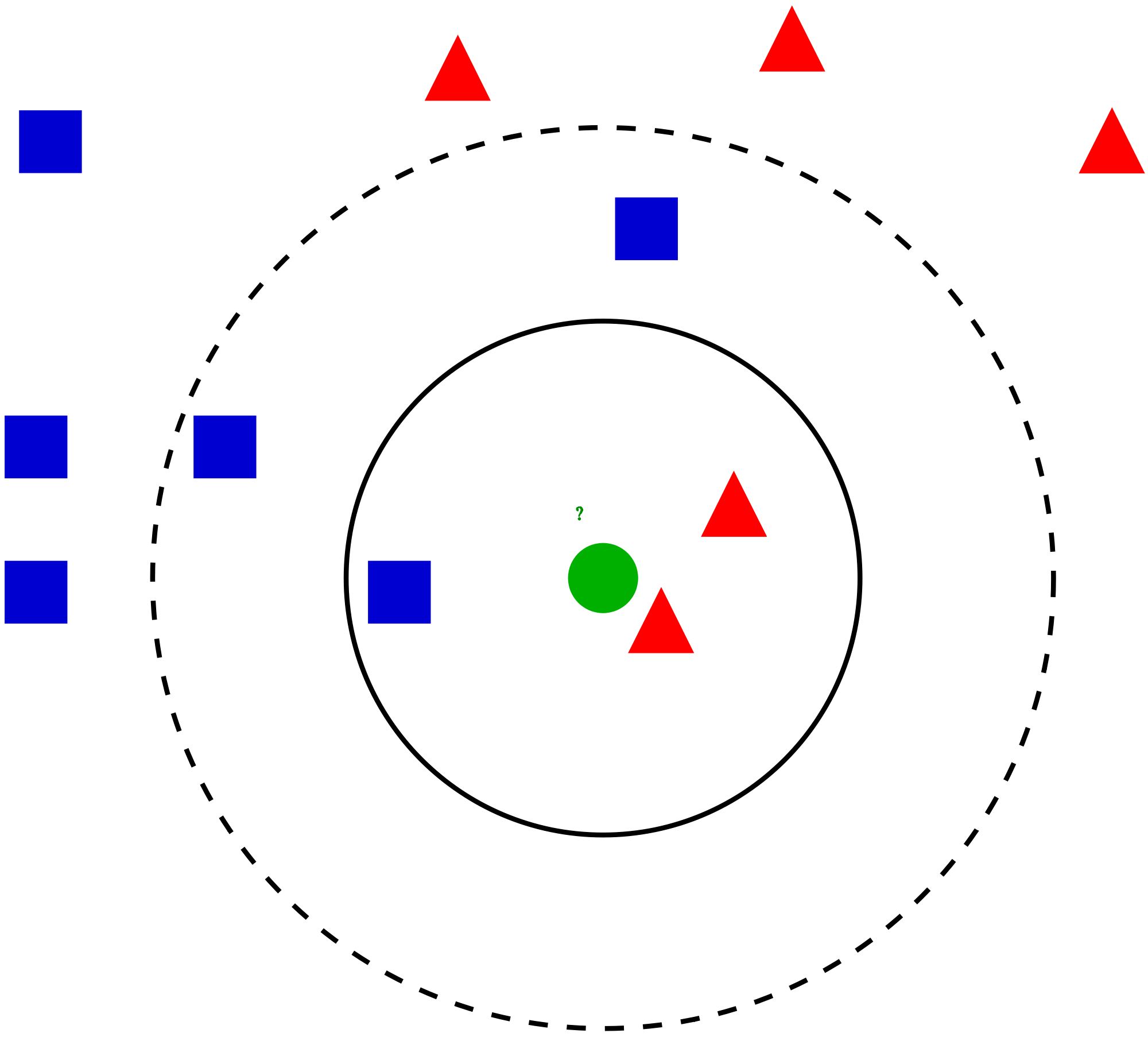
第一步：将训练数据输入到特征空间，并把待测数据也输入到该特征空间中（问号位置是该未知电影出现的镜头数的图形化展示）

在这里插入图片描述

计算待预测分类电影与所有已知的分类类别的电影的欧式距离

在这里插入图片描述

第三步: 从第二步中我们得到了训练数据集中所有电影与待预测电影的欧式距离，然后我们将这些电影按照距离的升序排序，取前k个电影，这里假设k=3，那么离待预测电影的k个最近的电影依次是:He’s Not Really into Dudes、Beautiful Woman 和California Man。而这三部电影全是爱情片，因此我们判定未知电影是爱情片

这种基于内存方法的主要优点是当新的训练数据出现时，分类器可以立即适应。缺点是新样本分类的计算复杂度与训练数据在最坏情况下的规模呈现线性关系，除非数据集只有很少的特征，而且算法实现采用有效的数据结构，如KD树。

此外，由于KNN实际上并没有训练的步骤， KNN算法在训练的过程只是简单的存储训练数据，所以我们不能丢弃训练样本。因此，如果要处理大型数据集，存储空间将面临挑战。

KNN三要素

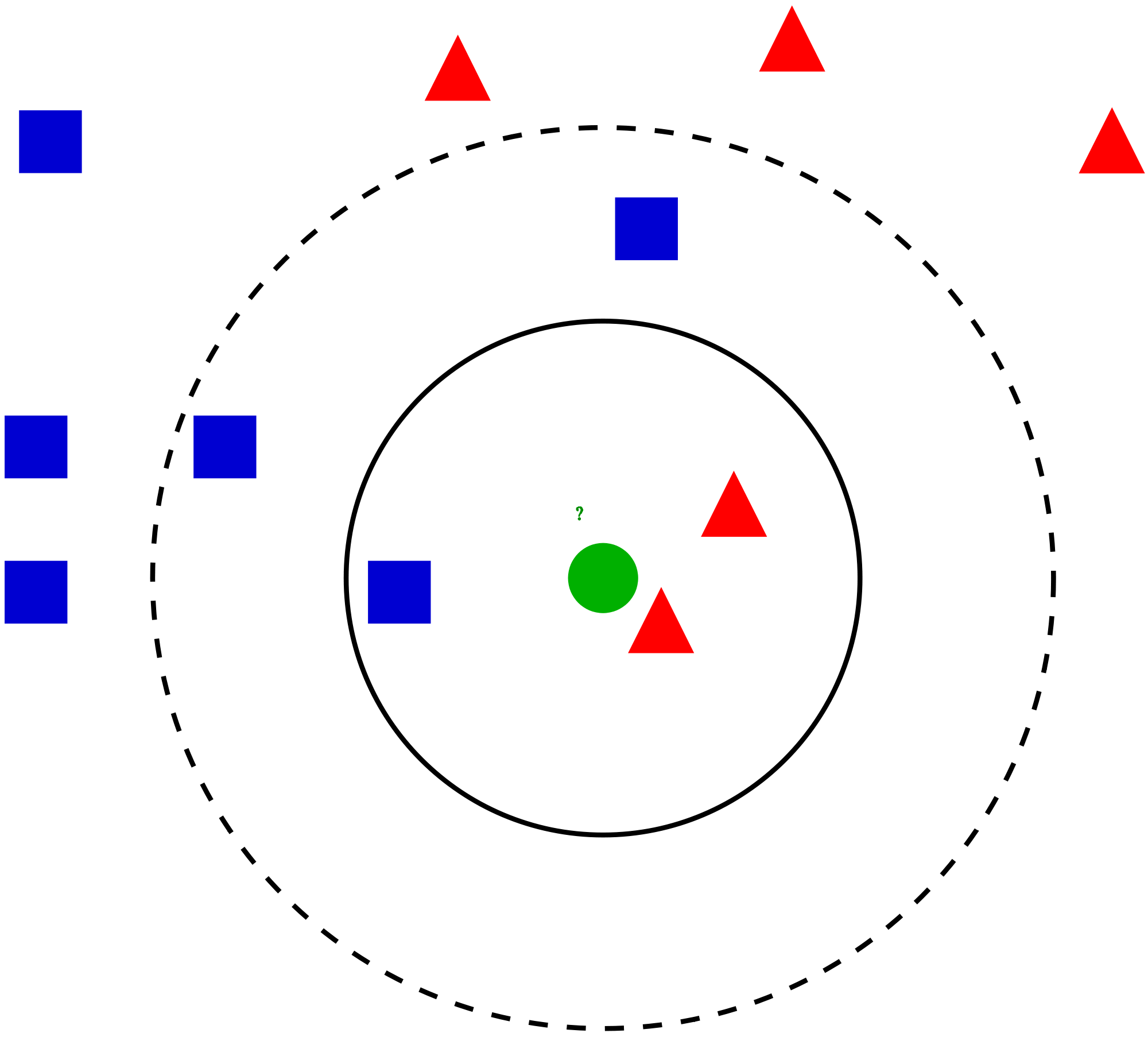
在这里插入图片描述

如上图中，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？

如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类；

如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。

在KNN算法中，非常重要的内容主要是三个因素：

k值的选择:对于K值的选择，一般根据样本分布选择一个较小的值，然后通过交叉验证来选择一个比较合适的最终值；当选择比较小的K值的时候，表示使用较小领域中的样本进行预测，训练误差会减小，但是会导致模型变得复杂，容易过拟合；当选择较大的K值的时候，表示使用较大领域中的样本进行预测，训练误差会增大，同时会使模型变得简单，容易导致欠拟合；

合理的选择k值对在过拟合和欠拟合之间找到恰当的平衡直观重要。必须确保选择适合于数据集中特征的距离度量。通常用简单的欧几里得来度量。例如，鸢尾花数据集中的花样本，其特征度量以厘米为单位。然后，如果用欧几里得距离度量相似度，那么对数据进行标准化是至关重要的，我们需要确保每个特征都对距离起着同样的作用

距离的度量:一般使用欧式距离(欧几里得距离)

决策规则:在分类模型中，主要使用多数表决法或加权多数表决法；在回归模型中，主要使用平均值法或加权平均值法。

在样本类别预测争执不下的情况下，用scikit-learan实现的KNN算法将更喜欢近距离样本的邻居，即加权多数表决法。如果邻居有相似的距离，该算法将选择在训练数据集中最先出现的分类标签。在二分类的情况下，为了避免待测样本在两个类别下具有相同的投票，所以我们更倾向于将k值设置为奇数。

范数

范数是把一个事物映射到非负实数，且满足非负性、齐次性、三角不等式，符合以上定义的都可以称之为范数，所以，范数的具体形式有很多种（由内积定义可以导出范数，范数还也可以有其他定义，或其他方式导出）.

范数理论是矩阵分析的基础，度量向量之间的距离、求极限等都会用到范数，范数还在机器学习、模式识别领域有着广泛的应用。范数可以理解为一个元素和零元的距离, 换言之, 范数诱导出了距离的定义, 因此我们可以认为赋范空间也是一种度量空间。

在这里我们可以简单形象的将范数理解为向量的长度，或者向量到零点的距离，或者相应的两个点之间的距离

L1范数:

$\|x\|_1=\sum_{i=1}^N\left|x_i\right|$

L1范数即向量每个维度的元素的绝对值之和

L2范数（欧式范数）：
$\|\mathbf{x}\|_2=\sqrt{\sum_{i=1}^N x_i^2}$

Euclid范数 (欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方。
$L\infty $与$ L-\infty $范数

$\infty$ 范数: || $\mathbf{x} \|_{\infty}=\max _i\left|x_i\right|$ ，即所有向量元素绝对值中的最大值。
$-\infty$ 范数: || $\mathbf{x} \|_{-\infty}=\min _i\left|x_i\right|$ ，即所有向量元素绝对值中的最小值。
LP范数

$\|\mathbf{x}\|_p=\left(\sum_{i=1}^N\left|x_i\right|^p\right)^{\frac{1}{p}} \quad \quad p\in [1, +inf)$ ，即向量元素绝对值的 $\mathrm{p}$ 次方和的 $\mathrm{p}$ 次幂，

当p为1时，该范数就是L1范数。当p为2时，该范数就是L2范数。

举一个简单的例子，一个二维度的欧几里得空间 $\mathbb{R}^2$ 就有欧氏范数。在这个向量空间的元素（譬如：
$(3, 7)$ ) 常常在笛卡尔坐标系中被画成一个从原点出发的箭号。每一个向量的欧氏范数就是箭号的长度，即向量的模长。

在p范数下定义的单位球（unit ball）都是凸集（convex set），简单地说，若集合A中任意两点的连线段上的点也在集合 $A$ 中，则 $A$ 是凸集），但是当 $0 < p < 1$ 时，在该定义下的unit ball并不是凸集（注意：我们没说在该范数定义下，因为如前所述， $0 < p < 1$ 时，并不是范数).下图展示了p取不同值时unit ball的形状。

在这里插入图片描述

根据P 的变化，范数也有着不同的变化，一个经典的有关P范数的变化图如下：

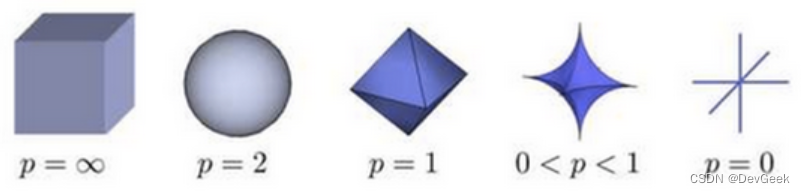
在这里插入图片描述

上图表示了p从无穷到0变化时，三维空间中到原点的距离（范数）为1的点构成的图形的变化情况。以常见的L-2范数（p=2）为例，此时的范数也即欧氏距离，空间中到原点的欧氏距离为1的点构成了一个球面。

距离的度量

闵可夫斯基距离（Minkowski distance）

闵氏距离不是一种距离，而是一组距离的定义。对应Lp范数，p为变参数。闵可夫斯基距离是衡量数值点之间距离的一种非常常见的方法，假设数值点 P 和 Q 坐标如下：
$P=(x_1,x_2,\ldots,x_n)\mathrm{~and~}Q=(y_1,y_2,\ldots,y_n)\in\mathbb{R}^n$
那么，闵可夫斯基距离的定义如下：
$dist(x_i, y_i)=\left(\sum_{i=1}^{n}|x_{i}-y_{i}|^{p}\right)^{1/p}.$

上述公式中的p是一个变参数

当p=1时，就是曼哈顿距离，

当p=2时，就是欧氏距离，

当p→∞时，就是切比雪夫距离，

根据变参数的不同，闵氏距离可以表示一类的距离。

该距离最常用的 p 是 2 和 1, 前者是欧几里得距离（Euclidean distance），后者是曼哈顿距离（Manhattan distance）。假设在曼哈顿街区乘坐出租车从 P 点到 Q 点，白色表示高楼大厦，灰色表示街道：

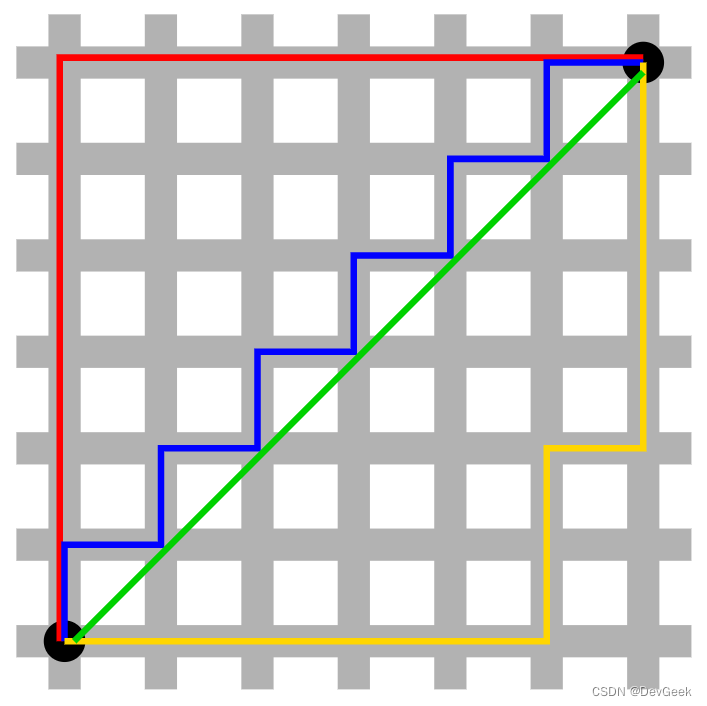
在这里插入图片描述

绿色的斜线表示欧几里得距离，如果要计算出租车从P点到Q点的所要行驶的路程，而在现实的城市中我们不可能之间从每个大楼中穿过，所以欧几里得距离在这里是不适用的。其它三条折线均指曼哈顿距离，并且这三条折线的长度是相等的。

曼哈顿距离（Manhattan distance）

曼哈顿距离的计算方式是将两点在每个坐标轴上的差值取绝对值，然后将所有坐标轴上的差值绝对值相加。这种距离计算方法得名于曼哈顿的城市布局，因为在曼哈顿的街道网格中，两点之间的行走距离通常是沿着网格线的，而不是直线。

当闵可夫斯基距离的变参数p=1的时候，对应的就是曼哈顿距离（对应L1范数），也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上，坐标 $\mathrm{P} 1 (\mathrm{x} 1, \mathrm{y} 1)$ 与坐标 $\mathrm{P} 2(\mathrm{x} 2, \mathrm{y} 2)$ 的曼哈顿距离为: $\left|x_1-x_2\right|+\left|y_1-y_2\right| \cdot$ ，要注意的是，曼哈顿距离依赖坐标系统的转度，而非系统在坐标轴上的平移或映射。

欧式距离（Euclidean distance）

当p=2的时候，对应的就是欧式距离（对应L2范数）：最常见的两点之间或多点之间的距离表示法，又称欧几里得度量，它定义为n维空间中两点之间的欧式距离。即：
$dist(x_i, y_i)=\sqrt{\sum_{i=1}^{n}(x_{i}-y_{i})^{2}}.$
也可以用向量的形式表示：
$dist(x_i, y_i)=\sqrt{(x_{i}-y_{i})^T(x_{i}-y_{i})}$

切比雪夫距离（Chebyshev distance）

当 p 趋近于无穷大时，闵可夫斯基距离转化成切比雪夫距离（Chebyshev distance）（对应$L\infty $范数）：
$\lim_{p\to\infty}\left(\sum_{i=1}^{n}|x_{i}-y_{i}|^{p}\right)^{\frac{1}{p}}=\max_{i=1}^{n}|x_{i}-y_{i}|.$
我们知道平面上到原点欧几里得距离（p = 2）为 1 的点所组成的形状是一个圆，当 p 取其他数值的时候呢？
在这里插入图片描述

KNN的决策边界

KNN的决策边界因k值而异

KNN中的k值是一个超参数。让我们改变k值，来看一下识别出的决策边界如何变化。

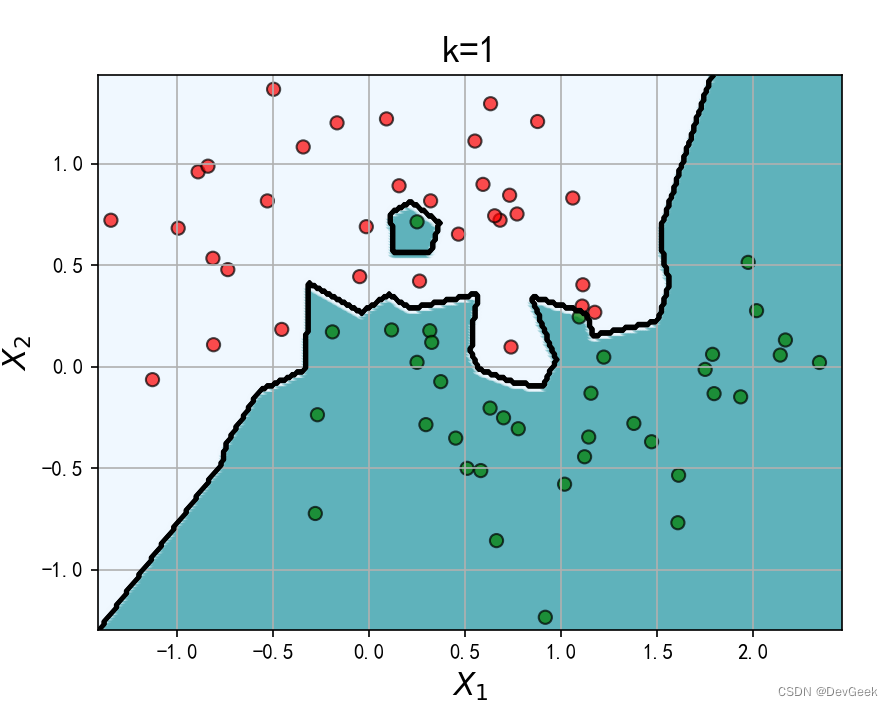
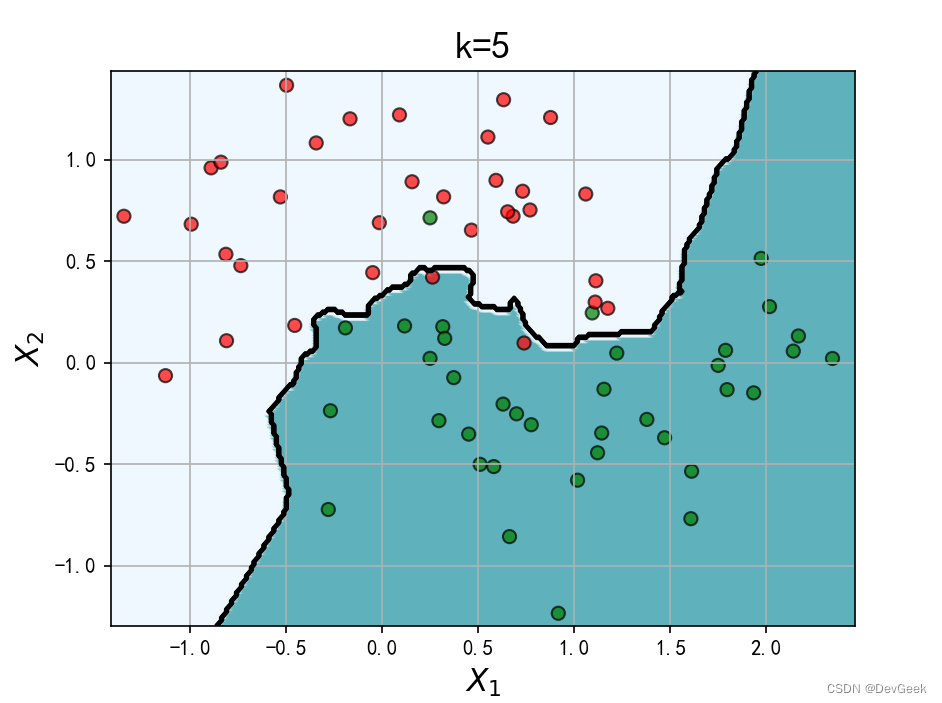
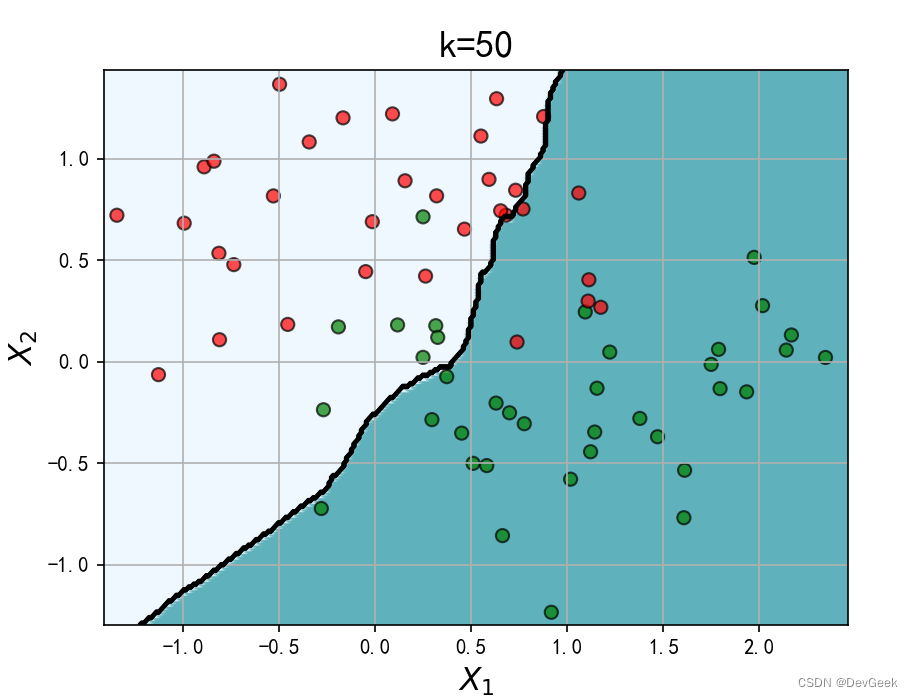
在这里插入图片描述

当k=1的时候，图中出现了一些像飞地一样的决策边界，模型偏向于将训练集中的所有样本都分正确，于是过于拟合了我们的训练数据，即发生了过拟合。中间的图的决策边界变得平滑，我们看不到在k=1时出现的飞地，所以k=5似乎比k=1更好。而当k=50时，背景为白色的区域内夹杂了一些错误的点，这是边界过于宽松导致的错误判断。

对于KNN来说， k越小模型越复杂，当k=1的时候模型最复杂。当k=n（训练样本数）的时候模型最简单，它只把输入的任何样本都预测为训练样本中占比最多的那个类别。

总而言之， k值的不同会导致学到的决策边界的外观发生变化。我们需要像其他算法一样对k值进行调优，得到最佳的k值

KNN分类预测规则

在knn分类应用中，一般采用多数表决法或加权多数表决法。
- 多数表决法:每个邻近的样本的权重都是相同的，也就是说最终的预测结果是k个样本中类别出现次数最多的那个类。
- 加权多数表决法:每个邻近样本的权重是不一样的，一般情况下采用权重和距离成反比的方式来计算，也就是说最终预测结果是出现权重最大的那个类别；比如右图中，假设三个蓝色点到待预测样本点的距离均为2，两个绿色点到待预测样本点距离为1，那么蓝色圆圈的最终类别为绿色。

KNN回归预测规则

在knn回归应用中，一般采用平均值法或加权平均值法。
平均值法:每个邻近样本的权重是一样的，也就是说最终预测的结果为所有邻近样本的目标属性值的均值；比如右图中，蓝色圆圈的最终预测值为：2.6；
加权平均值法:每个邻近样本的权重是不一样的，一般情况下采用权重和距离成反比的方式来计算，也就是说在计算均值的时候进行加权操作；比如右图中，假设上面三个点到待预测样本点的距离均为2，下面两个点到待预测样本点距离为1，那么蓝色圆圈的最终预测值为：2.43。(权重分别为: 1/7和2/7)
具体求法：我们首先求最近的k个样本的权重之和，即 $\frac{1}{2} \cdot 3+1 \cdot 2=\frac{7}{2}$ ，接着我们对权重和进行归一化，使总权重和为1，也就是最近的每个样本的权重都乘以 $\frac{2}{7}$ , 于是值为3的样本的权重为 $\frac{1}{2} \cdot \frac{2}{7}=\frac{1}{7}$ , 值为2的样本的权重为 $1\cdot \frac{2}{7}=\frac{2}{7}$ , 接着我们就将这几个样本所对应的值乘以相应的权重，然后进行加和， $\frac{1}{7} \cdot 3 \cdot 3+\frac{2}{7} \cdot 2 \cdot 2=\frac{17}{7} \approx 2.43$

具体过程：
1. 首先，选择一个适当的K值，表示要考虑的最近邻居的数量。
2. 对于给定的待预测样本，计算它与训练集中每个样本之间的距离。常用的距离度量方法包括欧几里德距离、曼哈顿距离等。
3. 选择与待预测样本距离最近的K个样本作为最近邻居。
4. 计算最近邻居与待预测样本之间的权重。常见的方式是使用距离的倒数作为权重，即距离越近，权重越大。也可以使用其他权重计算方法，例如高斯核函数。
5. 将每个最近邻居的目标属性值与对应的权重相乘，得到加权值。
6. 将所有加权值求和，并将其除以总权重的和，得到加权平均值。这个加权平均值即为回归的预测结果。
7. 可选地，对预测结果进行进一步处理，例如进行舍入、取整或应用其他后处理方法，以获得最终的回归结果。

Question——训练KNN模型需要进行特征标准化吗？

A：

KNN算法实现方式

KNN算法的重点在于找出K个最邻近的点，主要方式有以下几种：
- 蛮力实现(brute)：计算预测样本到所有训练集样本的距离，然后选择最小的k个距离即可得到K个最邻近点。缺点在于当特征数比较多、样本数比较多的时候，算法的执行效率比较低;
- KD树(kd_tree)：KD树算法中，首先是对训练数据进行建模，构建KD树，然后再根据建好的模型来获取邻近样本数据。
- 除此之外，还有一些从KD_Tree修改后的求解最邻近点的算法，比如：Ball Tree、BBF Tree、MVP Tree等。

KD-Tree–KNN中寻找最近邻的一个方法

我们举个例子，比如图书馆找书，如果书不按照种类进行划分，那么我们找书就要一个一个寻找，直到找到我们要找到的多本书，而KD-Tree就好比我们按照某些维度的差异性来将这些书所在区域进行划分，这样我们寻找的时候只需在某一区域内寻找即可，而不必大费周折、费时费力。

也就是说我们寻找最近的k个邻居，不再需要蛮力实现、遍历特征空间中的所有样本找出最近的k个样本，使用KD-Tree，我们只需在局部特征空间中寻找即可。

KD-Tree适用于数据量比较大的时候，它可以节省很多时间。

KD Tree是KNN算法中用于计算最近邻的快速、便捷构建方式。
当样本数据量少的时候，我们可以使用brute这种暴力的方式进行求解最近邻，即计算到所有样本的距离。但是当样本量比较大的时候，直接计算所有样本的距离，工作量有点大，所以在这种情况下，我们可以使用kd tree来快速的计算。

KD-Tree的构建方式

KD树采用从 $m$ 个样本的 $n$ 维特征中，分别计算 $n$ 个特征取值的方差，用方差最大的第 $k$ 维特征 $n_k$ 作为根节点。对于这个特征，选择取值的中位数 $n_{kv}$ 作为样本的划分点，对于小于该值的样本划分到左子树，对于大于等于该值的样本划分到右子树，对左右子树采用同样的方式找方差最大的特征作为根节点，递归即可产生KD树。

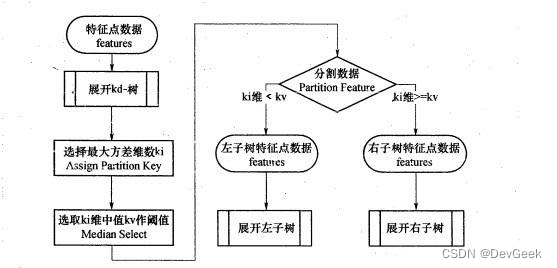
在这里插入图片描述

KD-Tree

二维样本: ${(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}$

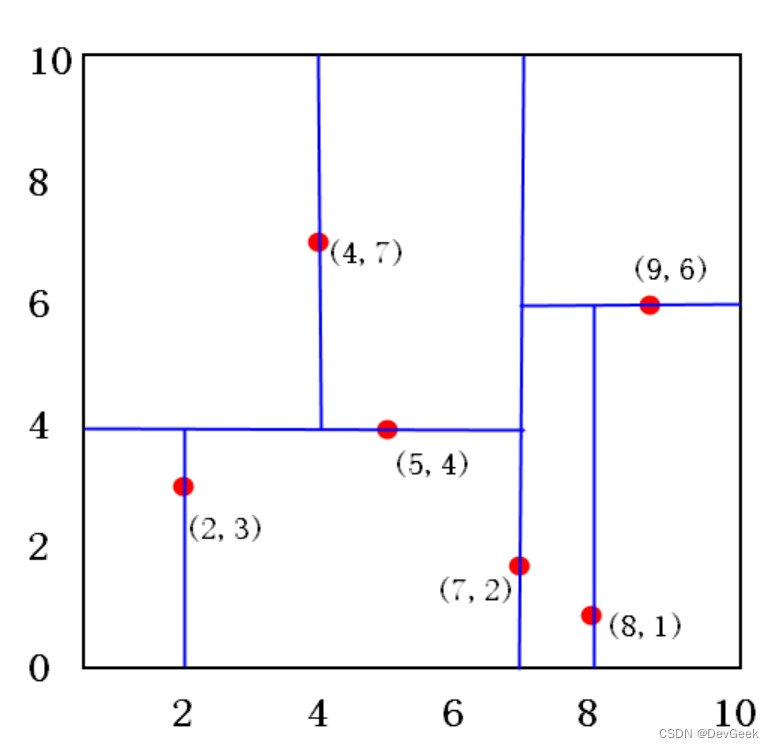
在这里插入图片描述

构建kd树案例

给定一个二维空间的数据集 $T=\left\{(2,3)^T,(5,4)^T,(9,6)^T,(4,7)^T,(8,1)^T,(7,2)^T\right\}$ ，画出特征空间的划分过程、kd树的构造过程。

第一步：选择 $x^{(1)}$ 轴，6个数据点的 $x^{(1)}$ 坐标上的数字分别是 $2, 5, 9, 4, 8, 7$ 。取中位数7 (不是严格意义的中位数，取较大的数)，以 $x^{(1)}=7$ 将特征空间分为两个矩形：

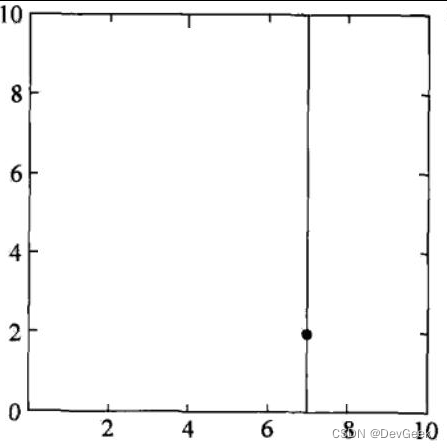
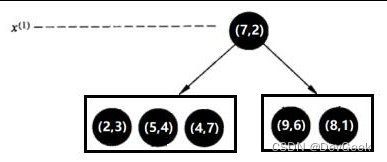
在这里插入图片描述

第二步：选择 $x^{(2)}$ 轴，处理左子树，3个数据点的x(2)坐标上的数字分别是3，4,7。取中位数4，以 $x^{(2)}=4$ 将左子树对应的特征空间分为两个矩形；处理右子树，2个数据点的 $x^{(2)}$ 坐标上的数字分别是6,1。取6，以x(2)=6将右子树对应的特征空间分为两个矩形：

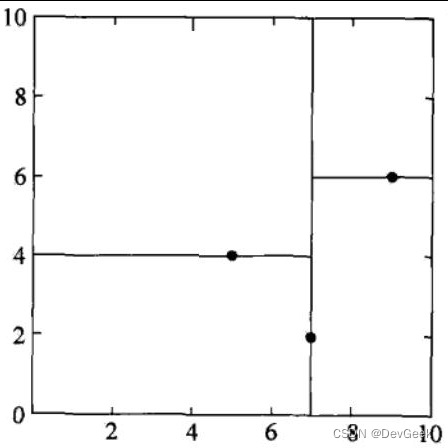
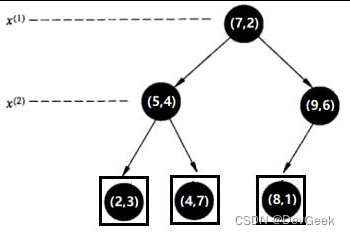
在这里插入图片描述

第三步： $x^{(1)}$ 轴，分别处理所有待处理的节点：

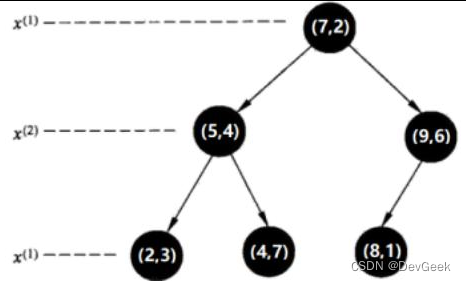
在这里插入图片描述

KD tree查找最近邻

当我们生成KD树以后，就可以去预测测试集里面的样本目标点了。对于一个目标点，我们首先在KD树里面找到包含目标点的叶子节点。以目标点为圆心，以目标点到叶子节点中样本实例的最短距离为半径，得到一个超球体，最近邻的点一定在这个超球体内部。然后返回叶子节点的父节点，检查另一个子节点包含的超矩形体是否和超球体相交，如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。如果不相交那就简单了，我们直接返回父节点的父节点，在另一个子树继续搜索最近邻。当回溯到根节点时，算法结束，此时保存的最近邻节点就是最终的最近邻。

找到所属的叶子节点后，以目标点为圆心，以目标点到最近样本点(一般为当前叶子节点中的其它训练数据或者刚刚经过的父节点) 为半径画圆，从最近样本点往根节点进行遍历，如果这个圆和分割节点的分割线有交线，那么就考虑分割点的另外一个子树。如果在遍历过程中，找到距离比刚开始的样本距离近的样本，那就进行更新操作。

一直迭代遍历到根节点上，结束循环找到最终的最小距离的样本。
在这里插入图片描述

维数诅咒

因为维数诅咒，KNN易于过拟合，了解这一点非常重要。当固定规模的训练集的维数越来越大时，特征空间将会变得越来越稀疏，这种现象被称为维数诅咒。直观地说，可以认为即使是最近的邻居在高维空间的距离也很远，以至于无法合适地估计。

正则化是一种避免过拟合的一种方法。然而，在不适用正则化的模型中，如决策树和KNN，可以利用特征选择和降维技术来避免维数诅咒。

注意

当数据量较小或维度较小时，KNN 的效果很好，但是当数据量较大或维度较大时，我们就需要考虑其他方法。

首先看一下数据量较大的情况。由于要处理大量的训练数据，所以分类将变慢。这是由于在对未知数据进行分类时，KNN 需要在大量的训练数据上进行近邻搜索以找到最近的点。这就意味着 KNN 需要同时存储大量的训练数据，也就意味着需要存储容量。为了高效地进行近邻搜索，人们经常借助于和利用KD-Tree结构存储训练数据的技术，但一般来说，KNN 不适合处理大规模的训练数据。

KNN 也无法很好地学习高维数据。KNN 起作用的前提是“只要拥有的训练数据多，就能在未知数据的附近发现训练数据”这一假设。这个假设叫作渐近假设，但对于高维数据来说，这个假设不一定成立。对于高维的音频和图像数据，我们需要考虑其他方法。

虽然我们也可以使用KD-Tree的方式提高近邻搜索的速度，但对于大规模的数据，建议还是使用其他算法。

scikit-learn库中KNN算法的参数说明

$n_neighbors 邻近数目, 默认为 5 algorithm 计算方式, 默认为auto, 可选参数: auto、ball_tree、kd_tree、brute; 推荐选择kd_tree leaf_size 在使用KD_Tree、Ball_Tree的时候, 允许存在最多的叶子数量, 默认为30 metric 样本之间距离度量公式, 默认为minkowski (闵可夫斯基) ; 当参数 p 为 2 的时候, 其实就是欧几里得距离 p 给定minkowski距离中的p值, 默认为2 \begin{array}{|c|c|} \hline \text { 参数 } & \text { KNeighborsRegressor } \\ \hline \text { weights } & \text { 样本权重, 可选参数: uniform(等权重)、distance(权重和距离成反比, 越近影响越强); 默认为uniform } \\ \hline \text { n\_neighbors } & \text { 邻近数目, 默认为 } 5 \\ \hline \text { algorithm } & \text { 计算方式, 默认为auto, 可选参数: auto、ball\_tree、kd\_tree、brute; 推荐选择kd\_tree } \\ \hline \text { leaf\_size } & \text { 在使用KD\_Tree、Ball\_Tree的时候, 允许存在最多的叶子数量, 默认为30 } \\ \hline \text { metric } & \text { 样本之间距离度量公式, 默认为minkowski (闵可夫斯基) ; 当参数 } \mathrm{p} \text { 为 } 2 \text { 的时候, 其实就是欧几里得距离 } \\ \hline \mathrm{p} & \text { 给定minkowski距离中的p值, 默认为2 } \\ \hline \end{array}$

import numpy as np
import pandas as pd
from sklearn.neighbors import KDTree
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import joblib


class KNN(object):
    def __init__(self, K, with_kd_tree=True):
        self.kd_tree = None
        self.X_train = None
        self.y_train = None
        self.k = K
        self.with_kd_tree = with_kd_tree

    def fit(self, X_train, y_train):
        """
        KNN 训练模型的过程，实际上就是存储数据
        :param X_train: 训练数据对应的特征矩阵X
        :param y_train: 训练数据对应的标签向量y
        :return:
        """
        ### 将数据转化为Numpy数组的形式进行存储
        self.X_train = np.asarray(X_train)
        self.y_train = np.asarray(y_train)
        if self.with_kd_tree:
            self.kd_tree = KDTree(X_train, leaf_size=10, metric='minkowski')
        return self

    def __fetch_k_neighbors(self, x):
        """
        1. 从训练数据集中获取k个离待测样本距离最近的训练样本数据
        2. 根据获取到的k个样本数据来预测出当前待预测样本的目标属性值
        :param x: 待预测的一条数据
        :return: 最近的k个邻居的label
        """
        if self.with_kd_tree:
            y_index = self.kd_tree.query([x], k=self.k, return_distance=False)[0]
            k_neighbors_label = []
            for i in y_index:
                k_neighbors_label.append(self.y_train[i])
            ### 返回k个邻居对应的标签
            return k_neighbors_label
        else:
            ### 列表 [[dis1, label1], [dis2, label2]...]
            listdistance = []
            ### 遍历训练数据集中的每一条样本， 得到训练集中每个样本与待测样本的距离dis
            for index, data in enumerate(self.X_train):
                dis = np.sum((np.array(data) - np.array(x)) ** 2) ** 0.5
                listdistance.append([dis, self.y_train[index]])

            ### 按照dis进行排序
            listdistance.sort()

            ### 选取k个邻居放进投票箱
            arr = np.array(listdistance[:self.k])[:, -1]
            ### 返回k个邻居对应的标签
            return arr

    def predict(self, X_predict):
        """
        :param X_predict: 待预测样本的特征属性X， X为矩阵
        :return:预测结果
        """

        ### 将预测的结果存储在一个list中
        result = []
        ### 统一使用numpy数组类型的数据
        X_ = np.asarray(X_predict)
        for data in X_:
            ### 1.从训练数据集中获取k个离待测样本最近的样本数据所对应的标签
            k_nearst_neighbors_label = self.__fetch_k_neighbors(data)
            ### 2.根据获取得到的k个样本数据对应的标签来预测待测样本所对应的目标属性值
            # 统计投票
            a = pd.Series(k_nearst_neighbors_label).value_counts()
            result.append(a.idxmax())
        return np.array(result, dtype=np.int32)

    def score(self, X_predict, y_true):
        """准确率"""
        y_hat = self.predict(X_predict)
        return np.mean(y_hat == y_true)

    # 存储模型
    def save_model(self):
        joblib.dump([self.X_train, self.y_train], 'knn.m')

    #
    def load_model(self, filename):
        X_, y_ = joblib.load(filename)
        self.fit(X_, y_)


if __name__ == '__main__':
    # 采用鸢尾花数据进行测试
    X, y = load_iris(return_X_y=True)
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)
    knn1 = KNN(K=5)
    knn1.fit(X_train, y_train)
    # knn1.load_model('knn.m')
    y_pre = knn1.predict(X_test)
    print(y_pre)  # [1 2 1 2 0 1 1 2 1 1 1 0 0 0 2 1 0 2 2 2 1 0 2 0 1 1 0 1 2 2]
    print(knn1.score(X_test, y_test))  # 1.0

    # 使用sklearn封装的knn算法
    knn2 = KNeighborsClassifier(n_neighbors=5)
    knn2.fit(X_train, y_train)
    print(knn2.score(X_test, y_test))  # 1.0