Introduction

在上一小节中讲到了Latent Variable Model（LAM），VAE。其主要思想就是将隐变量扩充为高维连续的分布，来增强模型的表达能力。而LAM模型中的核心困难是计算不出来，因为，而的维度过高算不出来。而根据Bayesian公式：

所以导致无法计算。而VAE那章介绍了近似推断的方法，使用一个简单分布来近似，其中还使用重参数化技巧来用一个神经网络来代替分布。

而在VAE中通过优化变分下界ELBO来达到最终优化的目的，而不是直接对Log似然函数进行优化。所以当然会有误差了。那么这将启发我们，可不可以绕过这个intractable的，使模型变得tractable。

Flow based Model

什么是flow model呢？首先用一张图来进行表示：

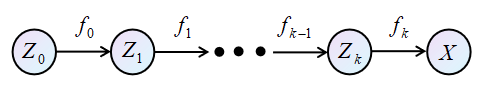
可以用一个简单的例子来简单的介绍Flow model。可以代表是当前的自己，人是比较复杂的，所以计算非常困难。而一般昨天的我，比今天要简单一点，但是很有可能，昨天的我依然很复杂，无法计算。那么，就不但的往前推，到了刚出生的时候，这时肯定是非常简单的，婴儿的世界里是非黑即白的，此时的分布很简单，可以被假设为。而这个过程：

就被称为“流”。因为流模型中初始分布是很简单的。极大似然估计中求的是：。那么下一个问题就是如何建立和之间的关系，将转换成求关于的函数。

Change of Variables

假设，。而，；是一个光滑可逆的函数。

那么可以得到：

根据不定积分的性质可以得到：

而且是光滑可逆的，所以，那么有

但是实际上和都是高维变量，所以是一个Jacobian Matrix。\textbf{熟悉矩阵的朋友应该知道，矩阵代表了一个变换，而矩阵行列式的值则代表了变换的尺度。}而在计算中我们关注的是矩阵变换的尺度，所以，

而最终的目的是想将完全用一个为自变量的函数来表达，所以要将用来表示。下面先写结论

这个结论是怎么来的呢？我们来看一个简单的例子，如下图所示：

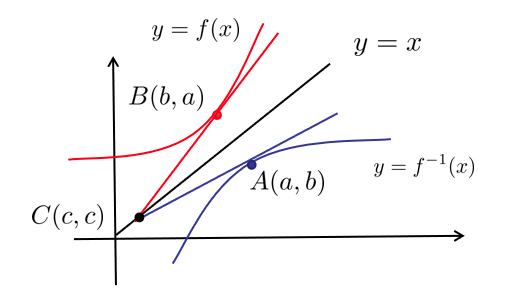
如图所示，，。那么有

而，

在本文举的例子中，

很显然有。这就是change of variables theorem。我们可以得到两个变量之间关于映射的转换为：

\textbf{那么，当训练完成之后，从中采样比较简单，通过上述公式，就可以得到，所以是可求解的。}如何学习呢？其实并不难，通过极大似然估计可以得到：

那么：

由于的逆很要求，上述梯度的计算还是比较简单的。然而，关于大矩阵行列式的计算并不美丽。后续有很多针对这点的改进方法，有兴趣的同学自行查看flow based的论文。

[1] ICLR 2015 NICE-Non-linear Independent Components Estimation

[2] ICLR 2017 Density estimation using Real NVP

[3] 2018 Glow: Generative Flow with Invertible 1×1 Convolutions

小结

本章主要介绍的是流模型的主要思想，在Latent Variable Model经常会遇到后验过于复杂无法求解的问题。流模型绕开了这个部分，对更简单的分布建模，然后建立原分布与简单分布之间的映射关系。个人觉得Stein变分梯度下降就有点流模型的影子在里面。在建立映射关系是用到了重要的change of variables theorem，并之后介绍了变化后的目标函数和梯度求解方法。

参考B站视频【机器学习】【白板推导系列】

更多干货，第一时间更新在以下微信公众号：