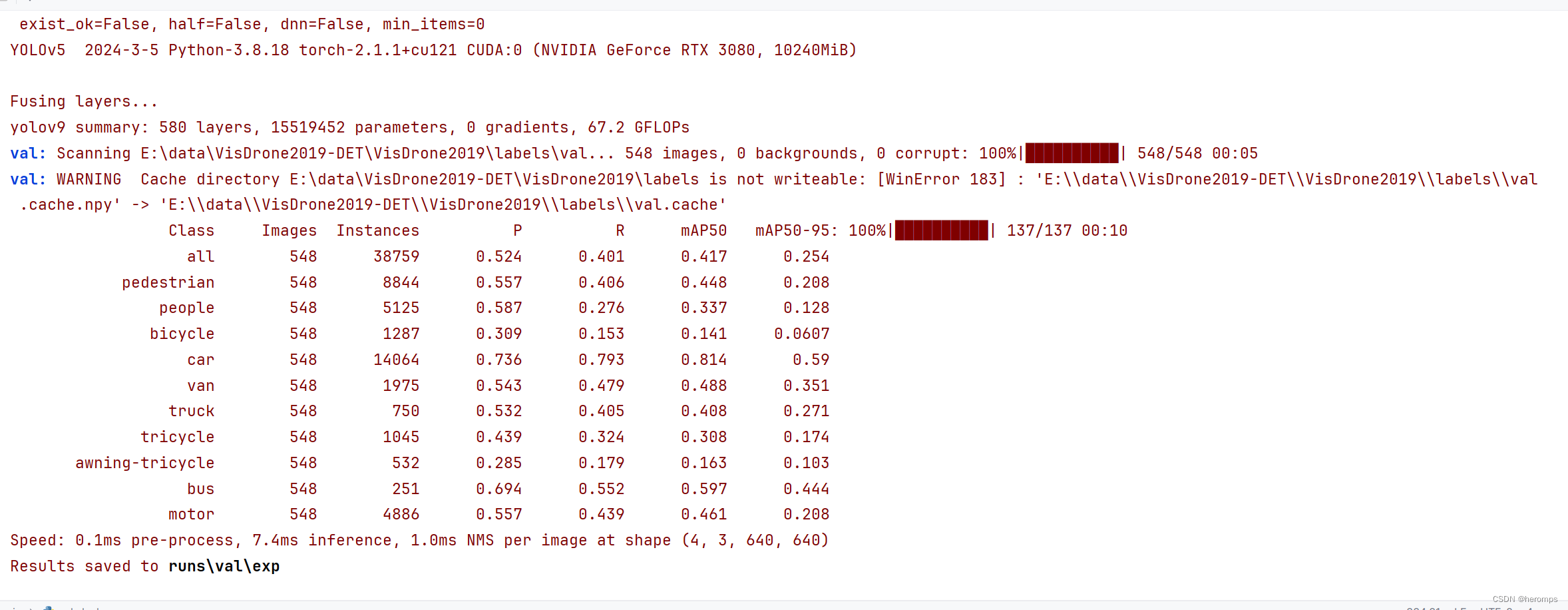
运行仿真时出错，仿真终止

原因: Simulink cannot solve the algebraic loop containing 'Gain' at time 1.0000000000000142 due to one of the following reasons: the model is ill-defined i.e., the system equations do not have a solution; or the nonlinear equation solver failed to converge due to numerical issues. To rule out solver convergence as the cause of this error, follow either of the suggested actions. If the error persists in spite of the above changes, then the model is likely ill-defined and requires modification.

（由于以下原因之一，Simulink无法求解时间为1.0000000000000142的包含“增益”的代数环:模型定义不清，即系统方程没有解;或者由于数值问题，非线性方程求解器不能收敛。要排除求解器收敛是导致此错误的原因，请遵循建议的操作之一。如果尽管进行了上述更改，错误仍然存在，则模型可能定义不清，需要修改。）

建议的操作

Reduce the RelTol parameter so that the solver takes smaller time steps.

基于simulink模型开发之代数环问题 - 知乎一、代数环问题的产生在建模开发过程中，经常需要将后端的结果输入到前端进行闭环运算，简单示例如下图所示： 当模型运行时，将会产生代数环错误，如下图所示： 二、代数环问题的解决方法1：配置更改（此方法不建…https://zhuanlan.zhihu.com/p/368929651?utm_id=0

如何解决simulink控制系统仿真中的代数环_simulink代数环错误怎么解决-CSDN博客文章浏览阅读1.3w次，点赞21次，收藏112次。1. 什么是代数环 在simulink仿真过程中，当输入信号直接取决于输出信号，同时输出信号也直接取决于输入信号时，由于数字计算的时序性，而出现的由于没有输入无法计算输出，没有输出也无法得到输入的“死循环” ，称之为代数环。 如下图所示，output = func（input+output）。初始时，由于没有output，所以不能计算func函数；但是为了得到output，又必须要计算func。如此往复就形成了代数环。2. 如何解决代数环——连续模型..._simulink代数环错误怎么解决https://blog.csdn.net/m0_59921410/article/details/124147968