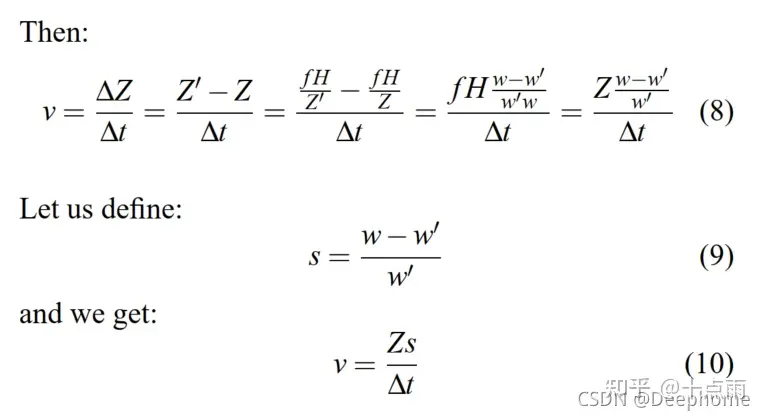238. 除自身以外数组的乘积
给你一个整数数组
nums,返回 数组answer,其中answer[i]等于nums中除nums[i]之外其余各元素的乘积 。题目数据 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。请 不要使用除法,且在
O(n)时间复杂度内完成此题。示例 1:
输入: nums = [1,2,3,4]输出: [24,12,8,6]示例 2:
输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 10(5)
-30 <= nums[i] <= 30保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内进阶:你可以在
O(1)的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)

class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> dp1(n);
vector<int> dp2(n);
dp1[0] = 1;
dp2[n - 1] = 1;
for (int i = 1; i < n; i++)
dp1[i] = dp1[i - 1] * nums[i - 1];
for (int i = n - 2; i >= 0; i--)
dp2[i] = dp2[i + 1] * nums[i + 1];
vector<int> answer(n);
for (int i = 0; i < n; i++)
answer[i] = dp1[i] * dp2[i];
return answer;
}
};获取数组长度:
int n = nums.size();
这里定义了一个整数 n 来存储输入向量 nums 的长度。
初始化前缀积和后缀积向量:
vector<int> dp1(n); vector<int> dp2(n);
定义了两个向量 dp1 和 dp2,大小均为 n。dp1 用于存储从左到右的累积乘积(前缀积),dp2 用于存储从右到左的累积乘积(后缀积)。
设置前缀积和后缀积的初始值:
dp1[0] = 1; dp2[n - 1] = 1;
为了方便计算,dp1 的第一个元素和 dp2 的最后一个元素被初始化为 1。
计算前缀积:
for (int i = 1; i < n; i++) dp1[i] = dp1[i - 1] * nums[i - 1];
从左到右遍历 nums,使用 dp1 来计算每个位置左侧所有元素的乘积。
计算后缀积:
for (int i = n - 2; i >= 0; i--) dp2[i] = dp2[i + 1] * nums[i + 1];
从右到左遍历 nums,使用 dp2 来计算每个位置右侧所有元素的乘积。
计算最终结果:
vector<int> answer(n); for (int i = 0; i < n; i++) answer[i] = dp1[i] * dp2[i];
定义了一个向量 answer,其大小为 n,用于存储最终结果。通过遍历 dp1 和 dp2 的每个元素并将它们相乘,得到 nums 中除了当前元素之外其余各元素的乘积。
时间复杂度和空间复杂度
时间复杂度:O(n)。整个算法中有三个独立的循环,每个循环都遍历了 n 次,但由于它们是顺序执行而非嵌套,所以总的时间复杂度是线性的。
空间复杂度:O(n)。除了输入数组 nums 外,主要额外空间消耗来自于两个长度为 n 的向量 dp1、dp2 和结果数组 answer。
560. 和为 K 的子数组
给你一个整数数组
nums和一个整数k,请你统计并返回 该数组中和为k的子数组的个数 。子数组是数组中元素的连续非空序列。
示例 1:
输入:nums = [1,1,1], k = 2 输出:2
示例 2:
输入:nums = [1,2,3], k = 3 输出:2
提示:
1 <= nums.length <= 2 * 10(4)
-1000 <= nums[i] <= 1000
-10(7) <= k <= 10(7)

class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int n = nums.size();
int sum = 0;
int ret = 0;
unordered_map<int, int> hash;
hash[0] = 1;
for (int i = 0; i < n; i++) {
sum += nums[i];
if (hash.count(sum - k))
ret += hash[sum - k];
hash[sum]++;
}
return ret;
}
};函数签名:
int subarraySum(vector<int>& nums, int k)
这行代码定义了一个函数 subarraySum,它接受一个整数向量 nums 和一个整数 k 作为参数,并返回一个整数作为结果。
获取数组长度:
int n = nums.size();
这里定义了一个整数 n 来存储输入向量 nums 的长度。
初始化累计和与计数器:
int sum = 0; int ret = 0;
sum 用于存储当前的累计和,ret 用于记录和为 k 的连续子数组的个数。
初始化哈希表用于存储累计和出现的次数:
unordered_map<int, int> hash; hash[0] = 1;
使用一个哈希表 hash 来存储各个累计和出现的次数,初始化时加入 0 的累计和出现了 1 次,这是为了处理那些从数组开头开始的、和为 k 的子数组。
遍历数组,更新累计和并检查:
for (int i = 0; i < n; i++) { sum += nums[i]; if (hash.count(sum - k)) ret += hash[sum - k]; hash[sum]++; }
遍历 nums 数组,对每个元素进行累加以更新 sum。然后检查 hash 中是否存在 sum - k 的键值,如果存在,说明找到了一个连续子数组其和为 k,将这个和的出现次数加到 ret 上。最后,将当前的 sum 出现次数加一,更新到 hash 中。
时间复杂度和空间复杂度
时间复杂度:O(n)。算法中有一个循环,遍历了一次数组 nums。
空间复杂度:O(n)。主要的额外空间消耗来源于哈希表 hash,在最坏的情况下,当所有的累计和都不同,它的大小可以达到 n。
974. 和可被 K 整除的子数组
给定一个整数数组
nums和一个整数k,返回其中元素之和可被k整除的(连续、非空) 子数组 的数目。子数组 是数组的 连续 部分。
示例 1:
输入:nums = [4,5,0,-2,-3,1], k = 5 输出:7 解释: 有 7 个子数组满足其元素之和可被 k = 5 整除: [4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
示例 2:
输入: nums = [5], k = 9 输出: 0
提示:
1 <= nums.length <= 3 * 10(4)
-10(4) <= nums[i] <= 10(4)
2 <= k <= 10(4)‘

class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k) {
int n = nums.size();
int sum = 0;
int ret = 0;
unordered_map<int, int> hash;
hash[0] = 1;
for (int i = 0; i < n; i++) {
sum += nums[i];
int x = (sum % k + k) % k;
if (hash.count(x))
ret += hash[x];
hash[x]++;
}
return ret;
}
};获取数组长度:
int n = nums.size();
这里定义了一个整数 n 来存储输入数组 nums 的长度。
初始化累积和与计数器:
int sum = 0; int ret = 0;
sum 用来累计 nums 中元素的和,ret 用来计数能被 k 整除的连续子数组数量。
初始化哈希表用于存储累积和模 k的结果出现的次数:
unordered_map<int, int> hash; hash[0] = 1;
使用一个哈希表 hash 来存储各个累积和模 k 的结果出现的次数,初始时加入 0 的累积和出现了 1 次,以便处理那些从数组开头开始且和能被 k 整除的子数组。
遍历数组,更新累积和模 k的结果,并检查:
for (int i = 0; i < n; i++) { sum += nums[i]; int x = (sum % k + k) % k; if (hash.count(x)) ret += hash[x]; hash[x]++; }
遍历 nums 数组,对每个元素进行累加以更新 sum。接着,计算调整后的累积和模 k 的结果,存储在 x 中。这里的 (sum % k + k) % k 确保 x 是一个非负数,因为直接 sum % k 可能会产生负数。如果 hash 中已存在 x,则表示之前已有累积和模 k 结果为 x 的子数组,这些子数组的结束点加上当前元素形成的新子数组也能被 k 整除,所以将 hash[x] 加到 ret 上。然后,将 x 对应的计数增加。
时间复杂度和空间复杂度
时间复杂度:O(n)。算法中包含一个遍历整个数组 nums 的循环。
空间复杂度:O(min(n, k))。哈希表 hash 存储的是累积和模 k 的结果,因此它的大小最多不会超过 k 的大小(在最坏的情况下,如果 k 小于 n),但也不会超过 n(如果每次迭代都产生一个不同的模数结果)。
总结
对于上述的问题,我们的解题思路是,希望先解决一个子问题,如果这个子问题解决了,整个问题只需要遍历一遍即可。解决子问题的时候,我们需要研究符合条件的时候的情况,所以我们先把符合条件的情况拿出来进行研究,转化等价关系。不断的定义解决问题需要的参数,整个问题的解决只需要不断的维护我们的定义的参数即可。
结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!