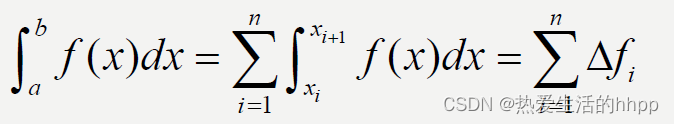目录
一.引言
二.数值微分
1.数值差分与差商
利用matlab观察差分与差商的区别:
例题:
二.数值积分
1.数值积分基本定理
2.常见的数值积分公式:
积分公式的精度:
3.数值积分的matlab实现
一.引言
在科学研究和工程计算中,常遇到下列情况:
(1)f(x)的原函数不能用初等函数形式表示,如
(2)f(x)由表格或图形(实验或测量数据)给出;(3)f(x)的原函数或导数很难求(复杂)。
从而,在实际应用中求导和求积公式很难解决上述函数的导数与积分问题!
因此,有必要研究求导和求积的数值计算方法(不再关心其解析表达式)!
二.数值微分
1.数值差分与差商
- 任意函数f(x)在x0点的导数是通过极限定义的:
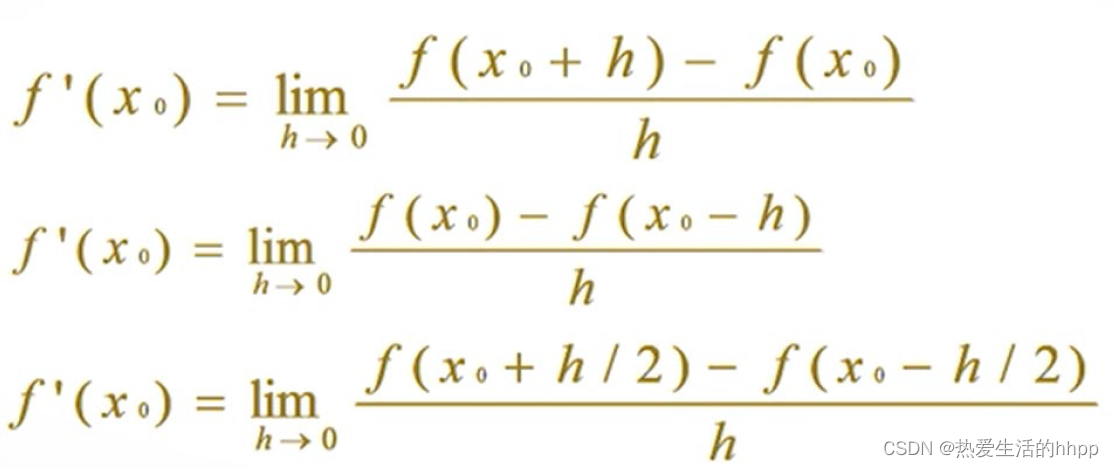
- 如果去掉极限定义中h趋向于0的极限过程,得到函数在x0点处以h为步长的差分:
(注意符号)
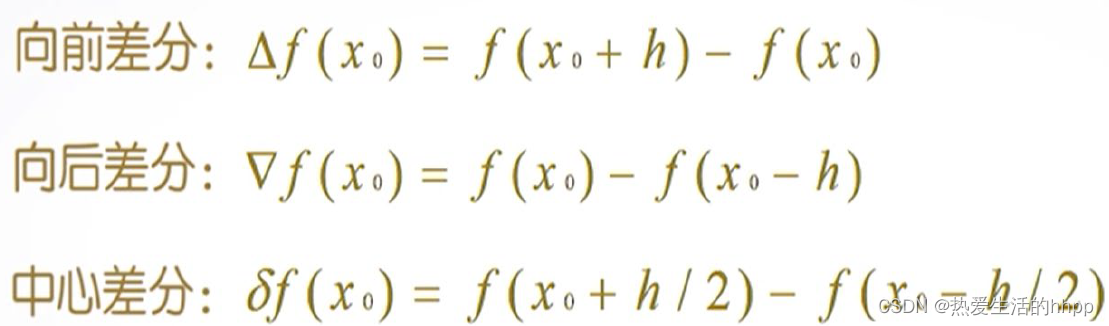
- 当步长h充分小时得到函数在x0点处,以h为步长的差商

结论:
函数f(x)在x0点的微分(dy)接近于函数在该点的差分()
而f(x)在x0点的导数()接近于函数在该点的差商(
)
利用matlab观察差分与差商的区别:
- Matlab预备知识:
注意:
diff函数计算的是向量元素的差分,故差分向量元素的个数比原向量少了一个;同样对于矩阵来说差分后矩阵比原矩阵少了一行或一列。另外计算差分之后,可以用f(x)在某点的差商作为其导数近似值。
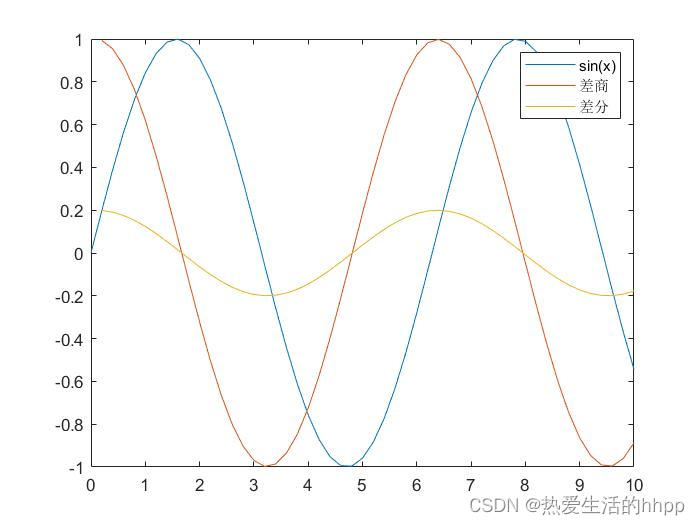
clc clear close all a = 1; h = 0.2; t = 0:h:10;%%确定横坐标,取一系列不连续的点 s = sin(t); v = diff(s)/h;%%差商 ds = diff(s);%%差分 figure plot(t,s) hold on plot(t(2:end),v) hold on plot(t(2:end),ds) legend('sin(x)','差商','差分')
差分与差商波峰与波谷相同,由分子决定
振幅由分母决定
例题:
1.设f(x) = sinx,在上随机采样,计算
的近似值,并于理论中
进行比较
clc
clear
close all
%%使用sort让0到2Π间的数据按顺序排列
x = [0,sort(2*pi*rand(1,4998)),2*pi]; %%确定x向量,其首尾元素分别为0和2Π
y = sin(x);
f1 = diff(y) ./ diff(x); %%利用diff函数求一阶向前差分,y的差分除以x的差分,得到差分向量商f1,作为导数近似值
f2 = cos(x(1:end-1)); %%向前差分删去一项
figure
plot(x(1:end-1),f1,'b*',x(1:end-1),f2,'r-');
legend('近似值曲线','理论值曲线','location','southeast')
d = norm(f1-f2); %%求近似值与理论值之间的范数 
d = 0.0441范数极小
2.二维函数的梯度计算
MATLAB提供了求梯度的函数gradient,其调用格式如下:

matlab代码实现:
clc
clear
close all
x = -3:0.2:3;
y = x';
f = x.^2 .* y.^3;%%定义出目标函数
surf(x,y,f) %%绘制三维图
xlabel('x')
ylabel('y')
zlabel('z')
[fx,fy] = gradient(f,0.2); %%计算所有点处梯度
%%计算(1,-2)处的梯度
x0 = 1;
y0 = -2;
t = (x == x0) & (y == y0);
indt = find(t); %%获取要寻找处的索引
f_grad = [fx(indt) fy(indt)]
%%输出结果
% f_grad =
% -16.0000 12.0400二.数值积分
1.数值积分基本定理
当被积函数的原函数无法用初等函数表示或被积函数是用表格形式给出的,这时,就需要用数值解法来求定积分的近似值。求定积分的数值方法多种多样:如梯形法、辛普森法、高斯求积公式等。它们的基本思想都是将积分区间[a,b]分成n个子区间
,这里i从1变化到n,其中
等于a ,
等于b,这样求定积分问题就分解为下面的求和问题:
2.常见的数值积分公式:

积分公式的精度:
要求代数精度越高越好
例:

任意次数小于3次的多项,均可用线性表示
- f(x)次数小于等于1次时,可以采用梯形公式
- Simpson公式(n=2)
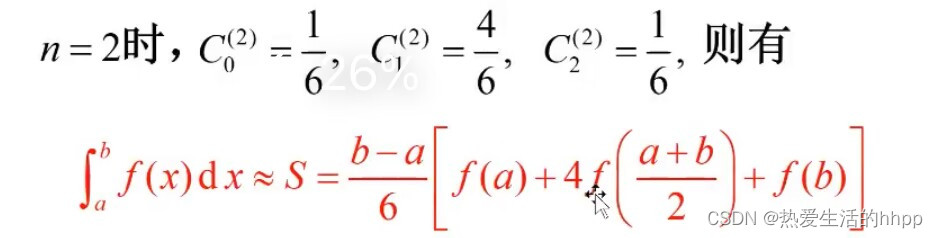
- 注:Simpson具有三次精度
为了提高精度,实际应用中常将积分区间划分成若干个小区间,在各小区间上采用低阶的求积公式(梯形公式或Simpson公式),再利用积分可加性,把区间积分加起来,得到新的求积公式,即复化求积公式


数值积分公式及龙贝格(Romberg)算法实现matlab
3.数值积分的matlab实现

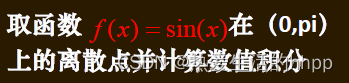
%%trapz和cumtrape
X = 0:pi/100:pi;
%%计算X的正弦值
Y = sin(X);
%%使用trapz对Y求积分
Q = trapz(X,Y)
%%Q =1.9998
q = cumtrapz(X,Y)另:多重数值积分的matlab实现