题目描述

题目描述
给定 n 个各不相同的无序字母对（区分大小写，无序即字母对中的两个字母可以位置颠倒）。请构造一个有 (n+1) 个字母的字符串使得每个字母对都在这个字符串中出现。
输入格式
第一行输入一个正整数 n。
第二行到第 (n+1) 行每行两个字母，表示这两个字母需要相邻。
输出格式
输出满足要求的字符串。
如果没有满足要求的字符串，请输出 No Solution。
如果有多种方案，请输出字典序最小的方案（即满足前面的字母的 ASCII 编码尽可能小）。
输入输出样例
输入 #1
4
aZ
tZ
Xt
aX
输出 #1
XaZtX
说明/提示
不同的无序字母对个数有限，n 的规模可以通过计算得到。

前置知识

欧拉路径

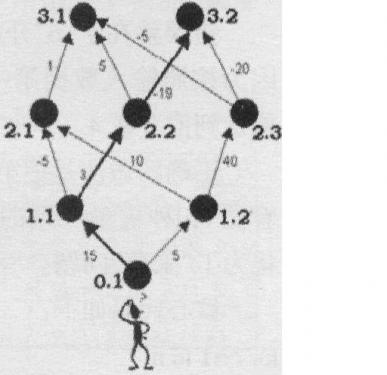
欧拉路径又被称为称为一笔画问题，就像这种

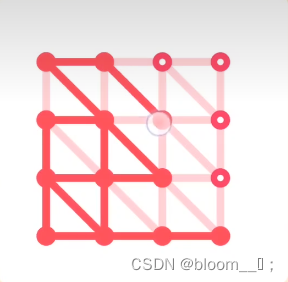
如果该图是欧拉图则可以一笔画完且不重复

定义

欧拉路径：从某一点出发恰每条边只通过一次的路径
欧拉回路：起点和终点相同的欧拉路径
欧拉图：具有欧拉回路的图
半欧拉图：具有欧拉路径的图

判断是否为欧拉图

无向图：

• 图中所有顶点的度都为偶数 – 欧拉图
• 图中有且仅有0个或两个奇数度的点 – 半欧拉图

奇数点为欧拉路起点

有向图：

• 图的所有顶点出度和入度都相等 – 欧拉图
• 有且仅有一个顶点入度比出度多 $1$，另有且只有一个顶点出度比入度多 $1$ – 半欧拉图

出度比入度多1的那个点为起点，入度比出度多1的那个点为终点

思路

因为题目说字母对可以颠倒顺序，所以可以直接将两个字母看作两个点构造一个无向图，然后直接在这个无向图上找一条字典序最小的欧拉路，首先需要判断这个图中奇数度点的个数，如果有两个奇数度的点，则把起点设置为ascii码小的那个奇数点。如果全是偶数点，也把起点设置成ascii码最小的点

code

#include <bits/stdc++.h>
using namespace std;

const int N=128;

int n;
// 邻接矩阵和出入度
int G[N][N], degree[N] = {0};
string ans;

// 找起点
int get_start() {
    int cnt = 0, res = 0;
    for (int i = 65; i < N; ++ i) 
        if (degree[i] & 1) {// 度数为奇数
            ++ cnt; 
            if (!res) res = i; // 记录起点，第一个奇数度的点
            if (cnt > 2) return -1; // 超过两个奇数点，没有欧拉回路
        }
    if (res && cnt != 2) return -1; 
    else if (res && cnt == 2) return res; // 有且仅有两个奇数度点
    // 如果没有度为奇数的点，则找字典序最小的一个有度的点
    int i;
    for (i = 65; i < N; ++ i) 
        if (degree[i])
            break;
    return i;
}

// 找欧拉路核心代码
void dfs(int x) {
    for (int i = 65; i < N; ++ i)
        if (G[x][i]) {
            G[x][i] = G[i][x] = 0;
            dfs(i);
        }
    ans.push_back(x);
}

int main() 
{
    cin.sync_with_stdio(false);
    cin >> n;
    for (int i = 0; i < n; ++ i) {
        char u, v;
        cin >> u >> v;
        G[u][v] = G[v][u] = 1;
        ++ degree[u]; ++ degree[v];
    }
    int start = get_start();
    if (start == -1) cout << "No Solution";
    else {
        dfs(start);
        reverse(ans.begin(), ans.end());
        cout << ans;
    }
    return 0;
}

参考

OI Wiki：欧拉图 - OI Wiki
B站UP主 【长腿羊の算法森林 】：【熊羊一锅鲜】Ep.17 一笔画问题：欧拉路径与欧拉回路