Machine Learning ---- Feature Scaling

news2024/11/16 5:43:30

一、What is feature scaling:：

二、Why do we need to perform feature scaling?

三、How to perform feature scaling:

1、Normalization:

2、Mean normalization:

3、Standardization (data needs to follow a normal distribution):

一、What is feature scaling：

Simply put, it is the process of normalizing the units of data, which results in significant differences in the non unit values of various data in the training dataset. However, we use normalization and other methods to stabilize the data range within a relatively small area.

二、Why do we need to perform feature scaling?

I have read many articles, and it's like how we often have a one-sided understanding of something due to its overly prominent side. For the more valuable side, we unconsciously lean towards the past. It is best for us to understand this point from a contour map:

Using the example said by Andrew Ng, let's assume that his housing price prediction is:

Total square meter: 300 square meters~2000 square meters	Number of rooms: 1 to 5
$w_1$ = 50	$w_2$ = 0.1
$w_1$ = 0.1	$w_2$ = 50

Meanwhile, assuming b=50, for a 2000 square meter, 5-room house, the normal price would be 500000 yuan:

At the same time, assuming b=50, for a 2000 square meter, 5-room house, the normal price is 500000 yuan. Therefore, when we bring in two different groups of w1 and w2 in the list, we can find that the factor with the larger value is: the total square * 50+room * 0.1, which gives a value of about 100000 yuan, while the other group is about 500000 yuan.

We can find that we prefer a smaller value with a larger corresponding coefficient. So, what is the relationship between this and gradient descent?

We can understand it from the contour map:

This is a contour map of $J(\vec{w},b)$ ,So we can take a look at how gradient descent may go if it needs to reach its minimum point:

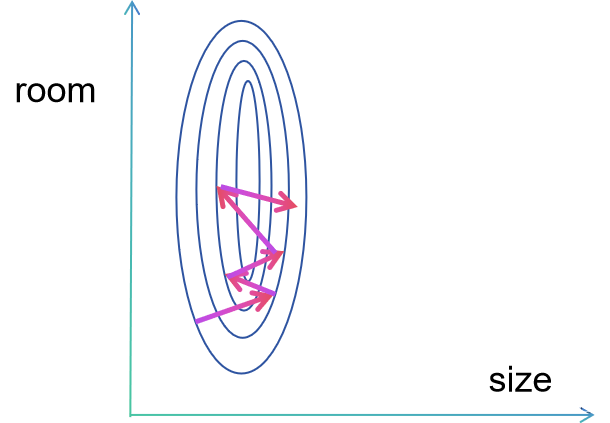
Due to the short axis range corresponding to size and the long axis corresponding to room, in order to obtain a minimum value that satisfies the condition through gradient descent, this situation may occur, leading to slower convergence. That's why we need to perform feature scaling, and if the image is not an ellipse but a circle, its effect is the best case.