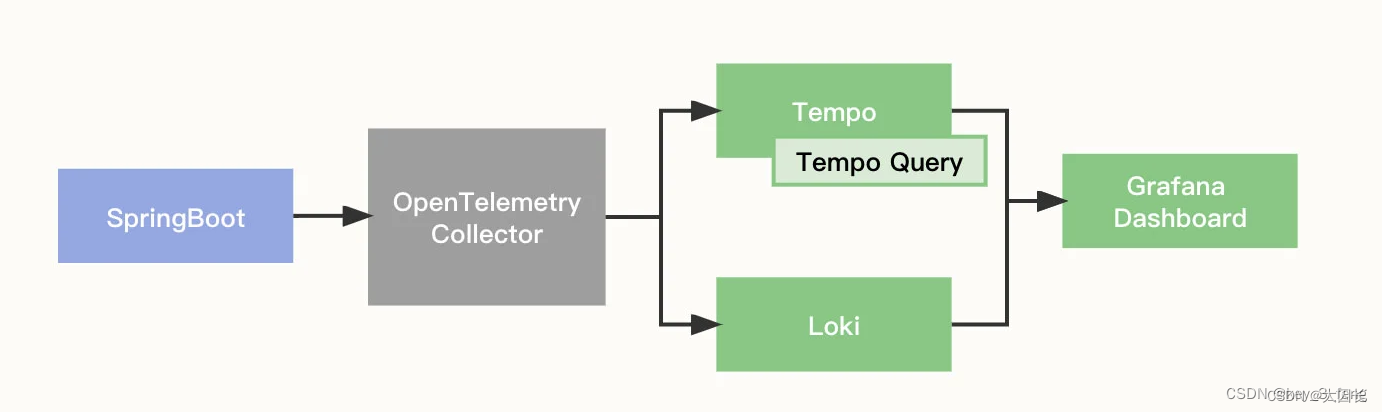
文章目录
- 问题
- 分析
问题
大家耳熟能详的最常见的问题就是 为什么不用 index 做 key ,在刚开始学习的时候,只是知道在 v-for 做循环遍历的时候需要加上唯一标识 key,但好像都是这么写的 v-for="(item,index) in dictList" :key="index",至于为什么在这里用index又不太好了,突然脑子空白了,直到我在掘金上榜的一篇文章中看到了答案,接下来我结合他的想法和我的想法用大白话讲两句

分析
-
我们在做渲染遍历的时候,是可以用
index作为key这样的一个唯一标识,但是当对代码有一定的理解后,是不建议用它的,那应该用什么呢?应该用遍历生成的每一项的唯一标识,例如:key="item,id"或者其他可以唯一标识的字段名。那么,新问题来了,为什么??? -
举一个例子,现在有一个列表list,我们已经将它渲染在了我们页面上,现在呢,要修改list,比如将某个值给他换了个数据,这个时候我们知道DOM要被重新渲染的,也就是我们常说的列表发生变化,DOM树重新被渲染,那我们频繁改变呢,而这个列表生成的虚拟DOM树又很大的情况下怎么办,浪费资源,浪费性能,怎么办!!!
-
尤雨溪 想到办法了,Vue 将新生成的新虚拟 DOM 与上一次渲染时生成的旧虚拟 DOM 进行比较,对比出是哪个虚拟节点更改了,找出这个虚拟节点,并只更新这个虚拟节点所对应的真实节点,而不用更新其他数据没发生改变的节点。这样一来是不是就性能好很多了
-
这个呢就是 Diff 算法,这时候有人会问:那跟index作为
key有什么关系。别着急,听我往下讲 -
运用这个 Diff 算法呢,我们节省了性能,节省了资源,那我绑定
index和item.id有区别吗 -
当然有,我们再举个例子,循环遍历生成的一个数组,我们在头部添加一个元素,这个索引
index是不是就要变,index 变了,是不是整个DOM就要重新渲染一遍, -
而我们用
item中的某个唯一标识去作为key时,Diff 算法就会进行遍历比较,发现其他节点并未变化,只是某个节点发生了变化,就不用去重新渲染其他DOM结构了,这也有点像 “有则改之无则加勉” 这句话。 -
那 Diff 算法是如何工作的呢
- 新旧虚拟DOM对比的时候,Diff 算法比较只会在同层级进行,不会跨层级比较。
- 首先比较两个节点的类型,如果类型不同,则废弃旧节点并用新节点替代。
- 对于相同类型的节点,进一步比较它们的属性。记录属性差异,以便生成相应的补丁。
- 如果两个节点相同,继续递归比较它们的子节点,直到遍历完整个树。
- 如果节点有唯一标识,可以通过这些标识来快速定位相同标识的节点。
- 如果节点的相同,只是顺序变化,不会执行不必要的操作。
-
以下是我总结的 不推荐使用索引作为
key,使用索引作为key可能会引发一些问题- 更新性能问题:当列表中的项目发生变化时,如果使用索引作为key,Vue可能会错误地识别和处理这些变化,导致出现意外行为和性能问题。
- 动态数据问题:如果列表中的项目可能会动态增加或减少,使用索引作为key可能导致Vue在更新时出现混乱,因为索引并不代表每个列表项的唯一身份。
- 稳定性问题:如果列表项的顺序可能发生改变,使用索引作为key可能导致Vue在重新渲染时出现错误,因为索引并不能保证列表项的唯一性。
- 相反,Vue也推荐使用每个列表项在数据集中的唯一标识作为key,比如一个具有唯一ID的数据库记录的ID字段。这样可以保证在列表发生变化时,Vue能够准确地识别每个列表项,并且能够更高效地进行更新和重渲染。
- 使用唯一标识作为key的好处是,它能够确保在更新过程中每个列表项都能正确地被跟踪和识别,从而避免潜在的问题。
- 总之,为了避免可能出现的问题,最好不要使用索引作为key,而是使用具有唯一性的标识符作为key,以确保Vue能够正确地管理和更新列表。
-
要是还没有理解 Diff 算法,我也总结了一波:Diff算法是用来比较两个文本或数据结构之间的差异,并找出它们之间的变化部分。Diff算法的工作原理可以简单概括为以下几个步骤:
- 分解:将输入的文本或数据结构分解成更小的片段,比如将文本拆分成单词或句子。
- 比较:对两个输入进行逐个元素的比较,找出它们之间的差异。
- 匹配:尝试找到最长的相同子序列,以减少差异的数量。
- 生成差异:根据比较结果生成描述性的差异表示,通常是一系列操作(如插入、删除、替换等)。
- 应用变更:根据生成的差异,可以在需要的地方进行相应的更新操作,以反映两个输入之间的变化。
通过Diff算法,我们可以高效地识别出两个文本或数据结构之间的变化,