40.组合总和II

题目

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明： 所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

解题思路

• 这题需要注意的点是数组中存在重复元素。比如 [1,1,2,2]，target=3；正常遍历会发现，存在多个重复的结果[1,2]。那么就能得出结论，第一次循环：第一个1选择后进行遍历得到一遍结果；第二次循环：这个1不可以选择。

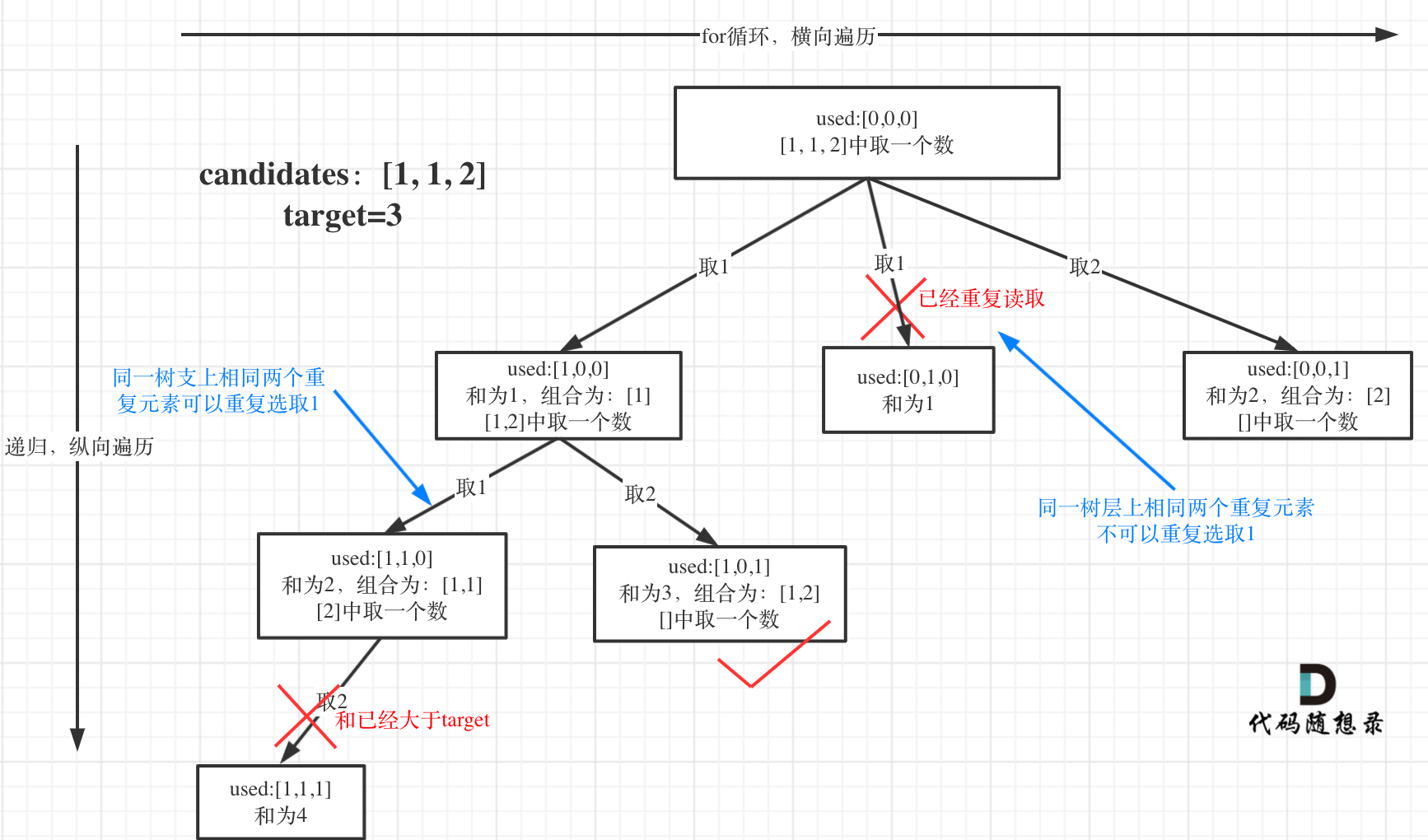
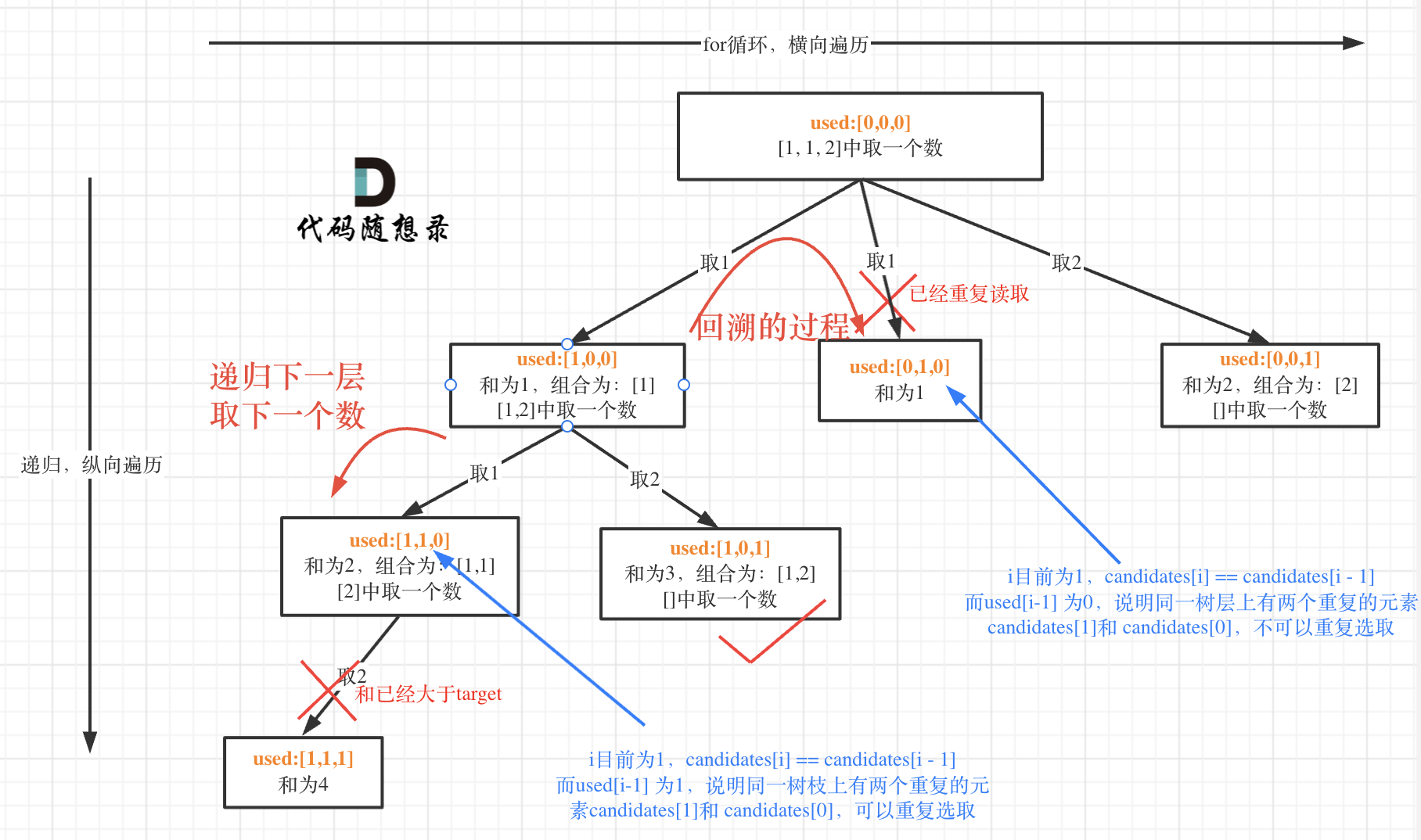
• 重点： 如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。

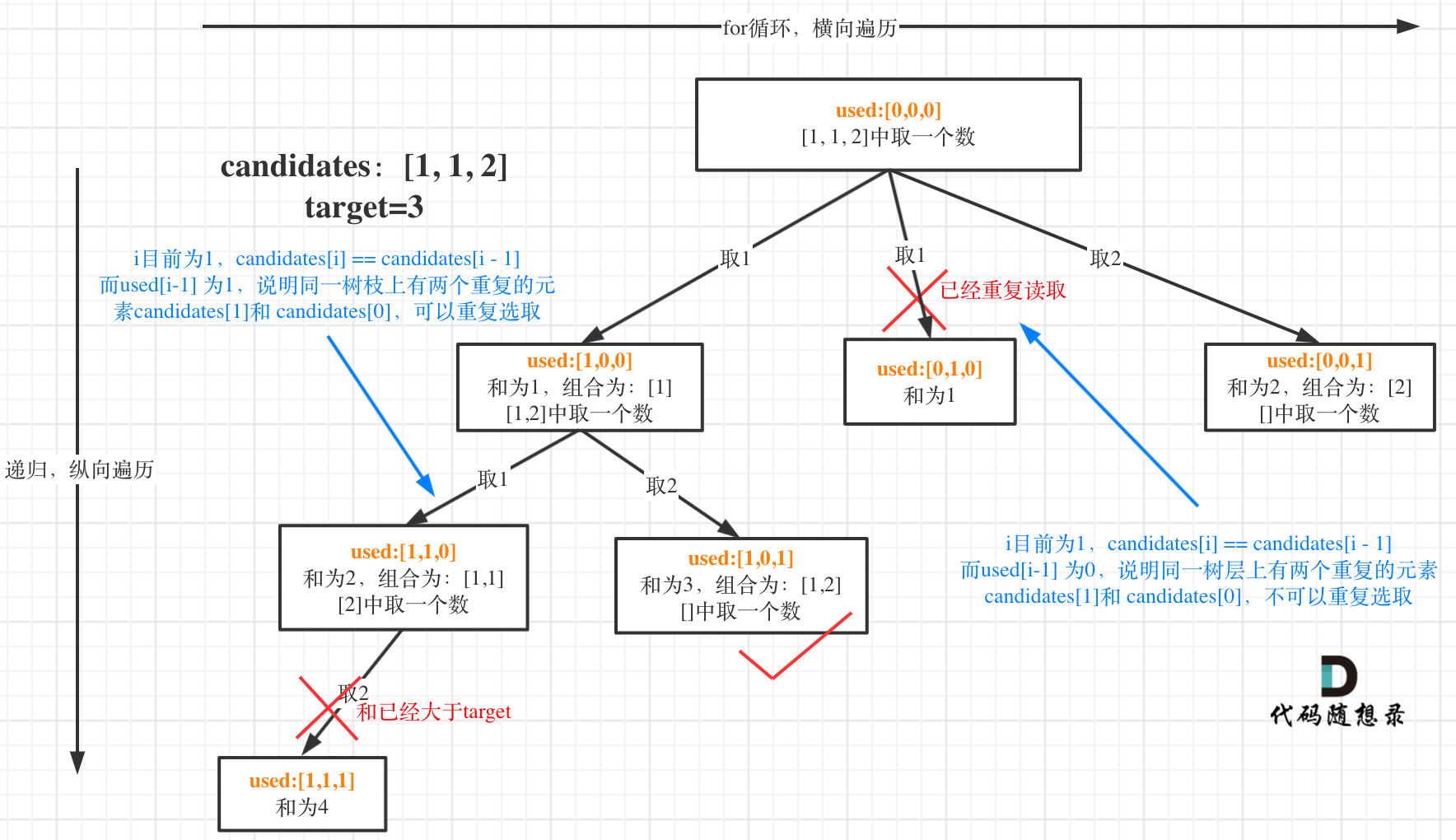
used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
used[i - 1] == false，说明同一树层candidates[i - 1]使用过

代码

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {
        if (sum == target) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            // 要对同一树层使用过的元素进行跳过
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
                continue;
            }
            sum += candidates[i];
            path.push_back(candidates[i]);
            used[i] = true;
            backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次
            used[i] = false;
            sum -= candidates[i];
            path.pop_back();
        }
    }

public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<bool> used(candidates.size(), false);
        path.clear();
        result.clear();
        // 首先把给candidates排序，让其相同的元素都挨在一起。
        sort(candidates.begin(), candidates.end());
        backtracking(candidates, target, 0, 0, used);
        return result;
    }
};