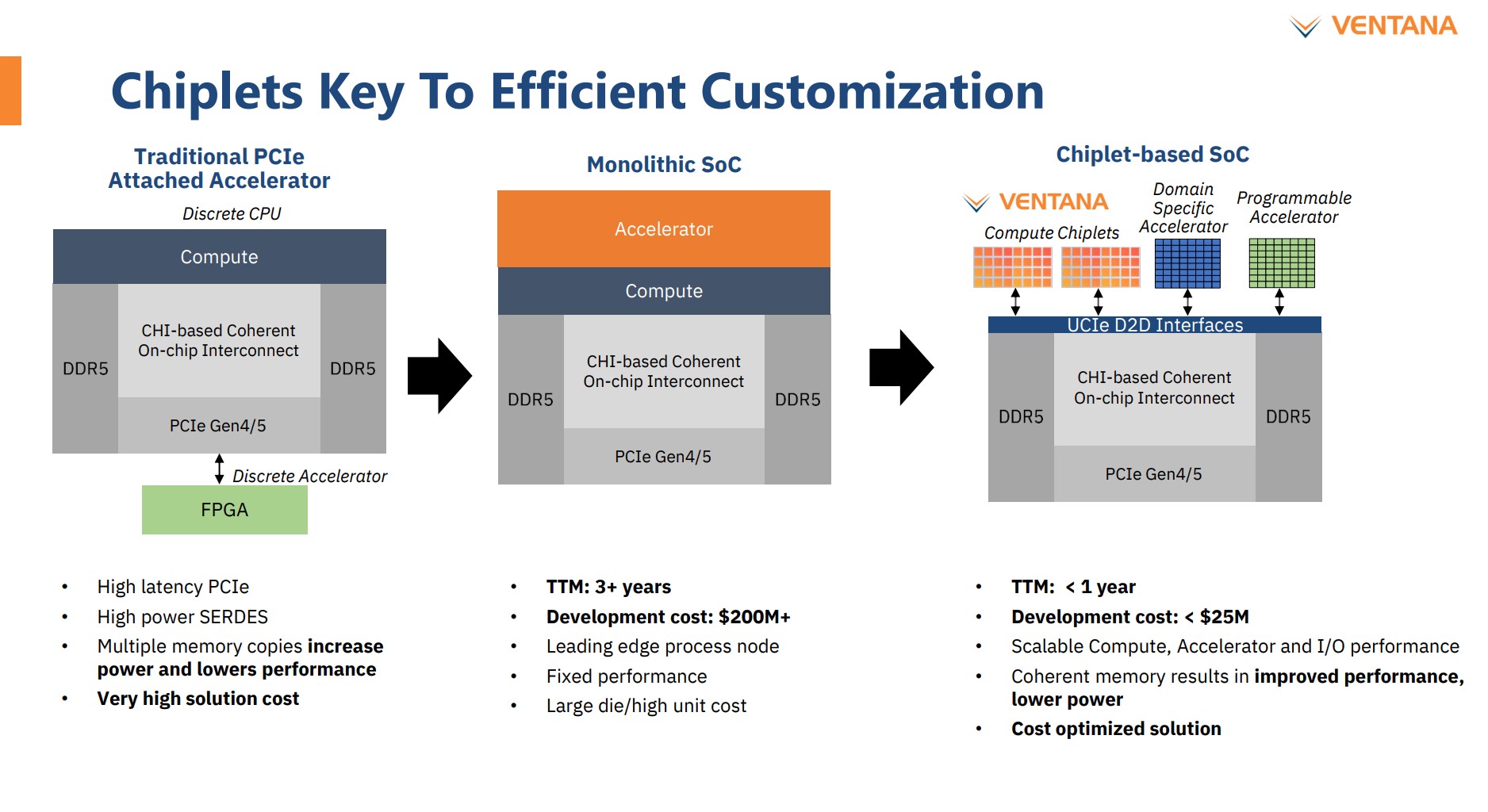
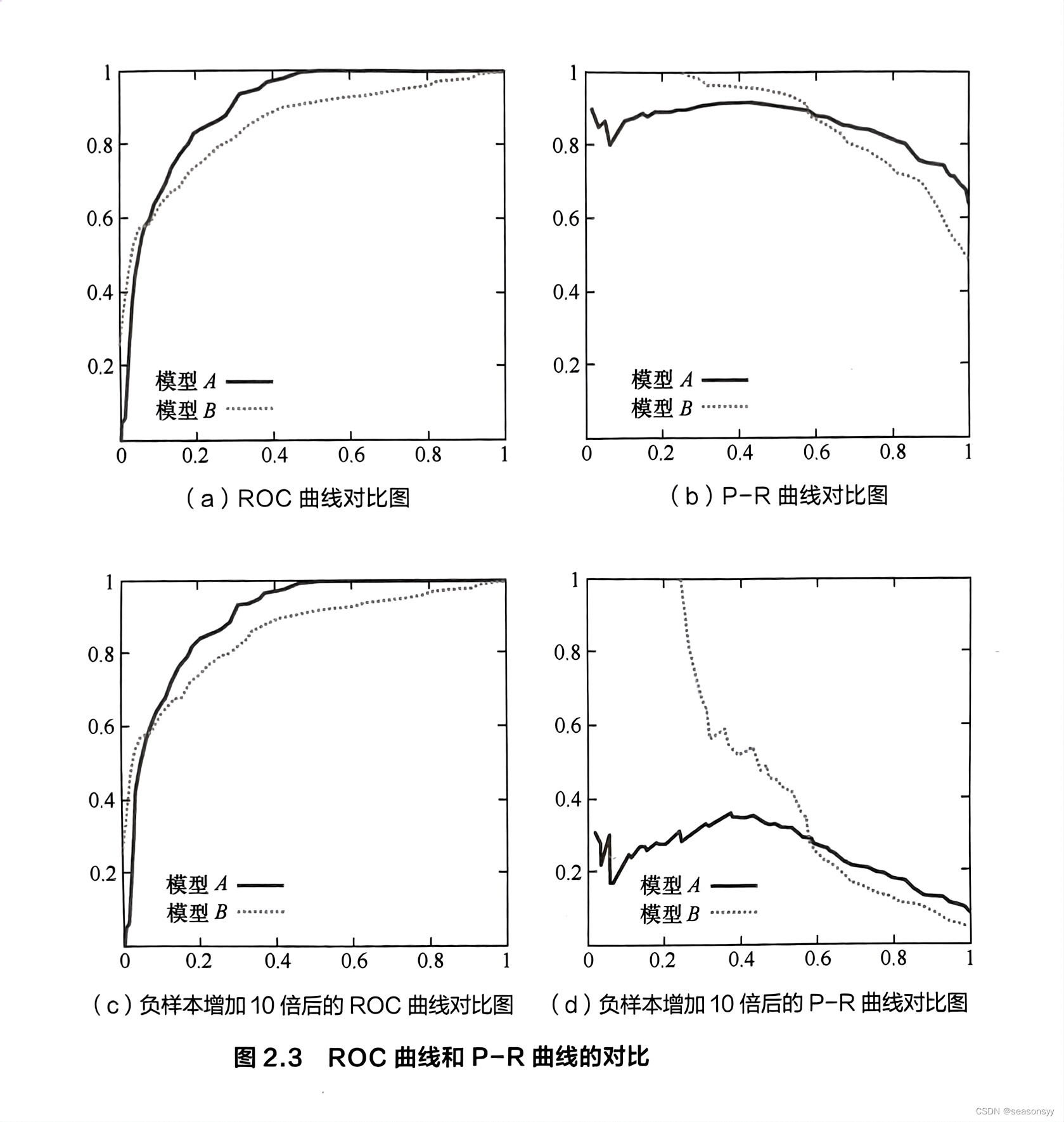
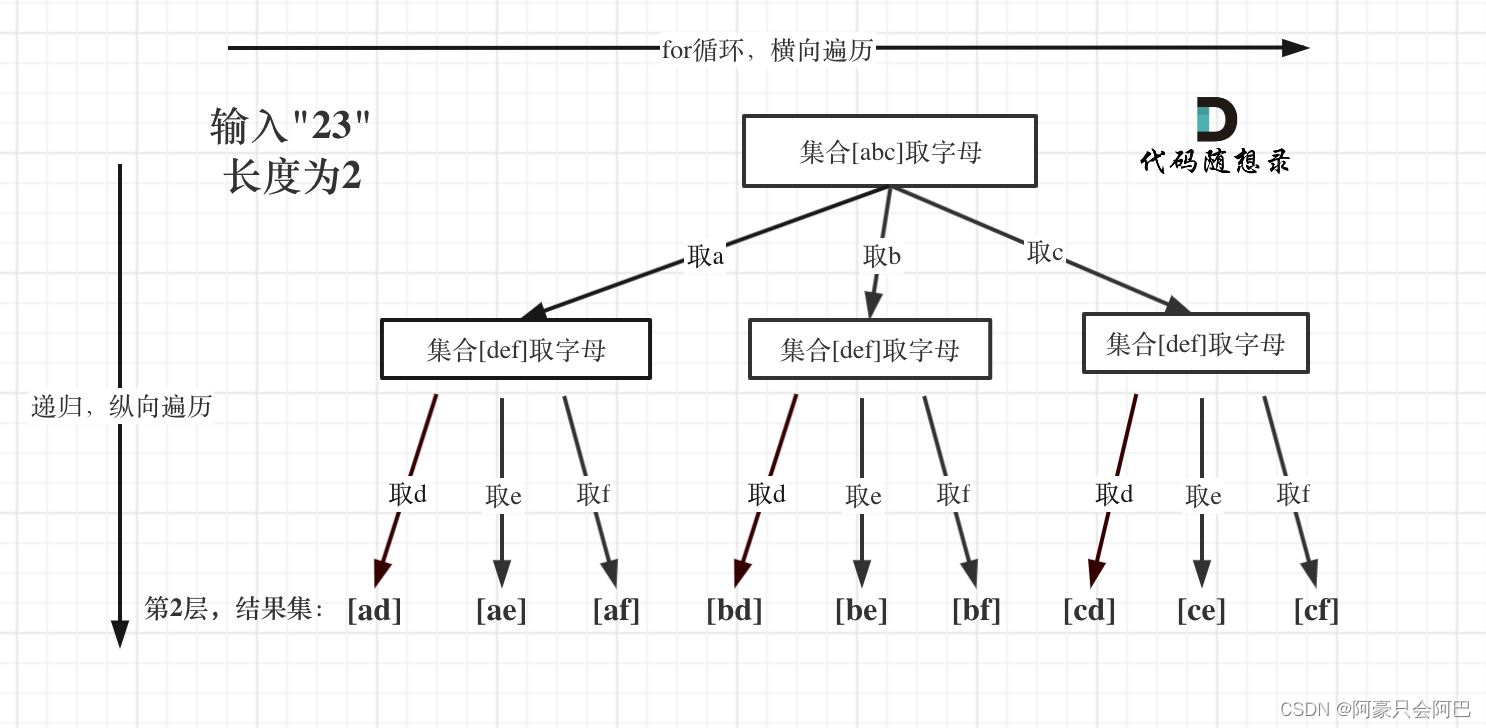
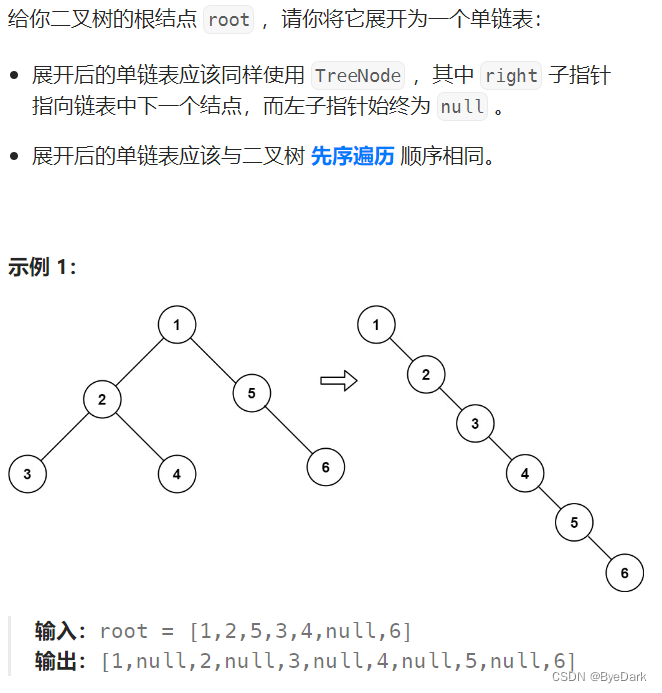
问题一：二叉树展开成单链表

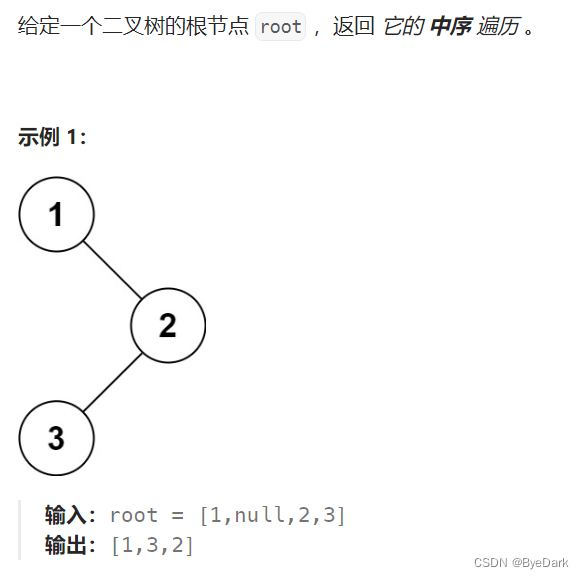
问题二：二叉树中序遍历

咋一看非常简单的两道题，但是如果我们加以一些限制，这两题就不简单了。对于这两道题，我们的空间复杂度都必须控制在O(1)。也就是说，迭代和递归全部失效了，这怎么办呢？
于是我们的主角Morris就出现了。

Morris算法 Morris 遍历算法是另一种遍历二叉树的方法，它能将非递归的中序遍历空间复杂度降为 O(1)。

Morris 中序遍历算法整体步骤如下：（力扣描述）

动画显示：
可视化的Morris

核心思想是什么？
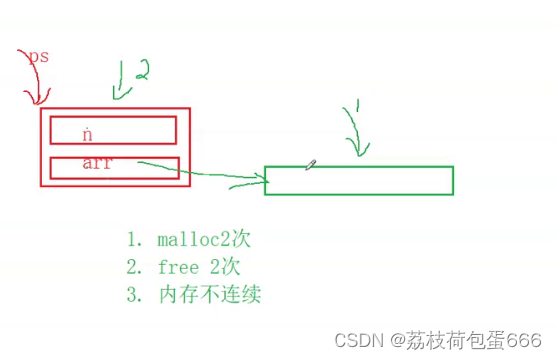
就是将叶子节点指向他的后驱节点。就是阉割版的线索二叉树啊。这样子我们就不需要通过栈来进行存储节点。直接遍历到尾部用指针指回去就行了。
那么第一题是不是也有想法了。我们怎么展开呢。找到一个节点的前驱节点，然后全部拼接到原来的右边，原来的右边节点直接拼到前驱节点的右边即可。
题目一代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public void flatten(TreeNode root) {
        //O(1)的Morris法，找curr的前驱进行拼凑
        TreeNode curr = root;
        TreeNode pre = null;
        while(curr!=null){
            if(curr.left!=null){
                pre = curr.left;
                while(pre.right!=null){
                    pre = pre.right;
                }
                //进行拼凑
                TreeNode left = curr.left;
                TreeNode right = curr.right;
                curr.right = left;
                curr.left = null;
                pre.right = right;
            }
            curr = curr.right;
        }
        return;
    }
}

题目二代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        //Morris
        List<Integer> ans = new ArrayList<>();
        TreeNode pre = null;
        while(root!=null){
            if(root.left!=null){
                pre = root.left;
                while(pre.right!=null&&pre.right!=root){
                    pre = pre.right;
                }
                if(pre.right==null){
                    pre.right = root;
                    root = root.left;
                }
                else{
                    pre.right = null;
                    ans.add(root.val);
                    root = root.right;
                }
            }else{
                ans.add(root.val);
                root = root.right;
            }
        }
        return ans;
    }
}