文章目录
- 前言
- 参考目录
- 学习笔记
- 0:引入介绍
- 1:APIs
- 1.1:API:加权有向边
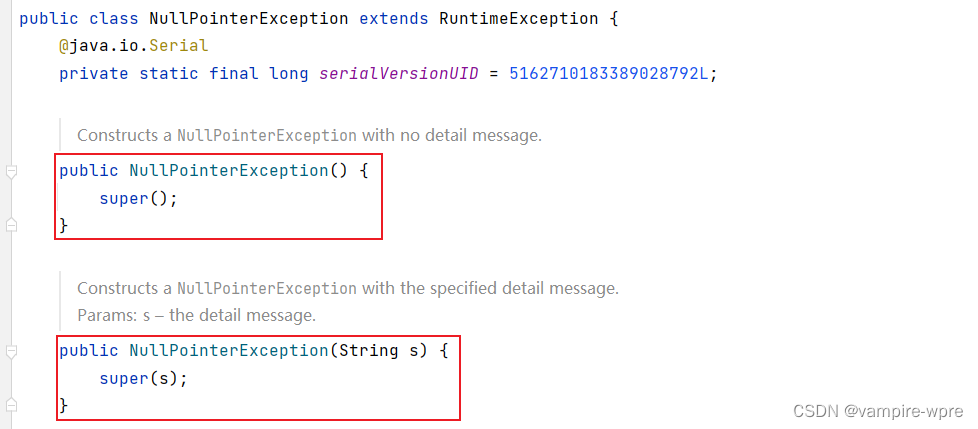
- 1.2:Java 实现:加权有向边
- 1.3:API:加权有向图
- 1.4:Java 实现:加权有向图
- 1.5:API:最短路径
- 2:最短路径性质
- 2.1:最短路径的数据结构
- 2.2:边的松弛 edge relaxation
- 2.3:最优性条件 optimality conditions
- 2.4:通用算法 generic shortest-paths algorithm
- 3:Dijkstra 算法
- 3.1:demo 演示
- 3.2:证明
- 3.3:Java 实现
- 3.4:计算图生成树
- 3.5:运行时间
- 4:无环加权有向图 edge-weighted DAGs
- 4.1:demo 演示
- 4.2:证明
- 4.3:Java 实现
- 4.4:最长路径
- 5:负权重 negative weights
- 5.1:失败尝试
- 5.2:负权重环 negative cycles
- 5.3:Bellman-Ford 算法
- 5.3.1:demo 演示
- 5.3.2:算法分析
- 5.4:成本开销小结
- 6:小结
前言
本篇主要内容包括:APIs、最短路径性质、Dijkstra 算法 、无环加权有向图 以及 负权重。
参考目录
- B站 普林斯顿大学《Algorithms》视频课
(请自行搜索。主要以该视频课顺序来进行笔记整理,课程讲述的教授本人是该书原版作者之一 Robert Sedgewick。) - 微信读书《算法(第4版)》
(本文主要内容来自《4.4 最短路径》) - 官方网站
(有书本配套的内容以及代码)
学习笔记
注1:下面引用内容如无注明出处,均是书中摘录。
注2:所有 demo 演示均为视频 PPT demo 截图。
注3:如果 PPT 截图中没有翻译,会在下面进行汉化翻译,因为内容比较多,本文不再一一说明。
0:引入介绍
加权有向图的最短路径(shortest paths in an edge-weighted digraph):
最短路径的应用:
![L15-44ShortestPaths_03]
- PERT/CPM:计划评审技术/关键路径法
- 地图路线规划
- 接缝雕刻(图像缩放中的内容感知算法)
- 纹理映射(计算机图形学中将图像纹理贴到三维模型表面的技术)
- 机器人导航技术
- TeX 中的排版设置
- 城市交通规划
- VLSI 芯片的最佳流水线设计
- 电话营销员操作员调度问题
- 电信消息的路由选择
- 网络路由协议(如 OSPF、BGP、RIP)
- 利用货币兑换市场中的套利机会
- 根据既定交通拥堵模式确定卡车最优行驶路线
Shortest path is a really interesting and important problem solving model. There’s all kinds of important practical problems that can be recast as shortest paths problems. And because we have efficient solutions to the shortest path, efficient algorithms for finding shortest paths, we have efficient solutions to all these kinds of problems.
最短路径是一个非常有趣且重要的问题解决模型。许多重要的实际问题都可以被重新表述为最短路径问题。正因为如此,我们拥有寻找最短路径的有效解决方案,即高效的最短路径算法,因此也就拥有了解决这类各种问题的有效方法。
最短路径的不同类型:
顶点类型:
- 单源:从一个顶点 s 到其他所有顶点。
- 单汇点:从每个顶点到另一个特定顶点 t。
- 源汇点:从一个顶点 s 到另一个顶点 t。
- 全对全:在所有顶点对之间。
边权重限制:
- 非负权重:所有边的权重都是非负数。
- 欧几里得权重:边权重基于欧几里得距离。
- 任意权重:边的权重可以是任意数值。
循环条件:
- 无有向循环:图中不存在有向循环。
- 无负权循环:图中不存在权重总和为负值的循环。
简化假设: 从顶点 s 到每个顶点 v 都存在最短路径。
1:APIs
1.1:API:加权有向边
1.2:Java 实现:加权有向边
edu.princeton.cs.algs4.DirectedEdge
![![image-20240315085631710]](https://img-blog.csdnimg.cn/direct/72925db556b34db0977660ea5efdba36.png)
![![image-20240315085644190]](https://img-blog.csdnimg.cn/direct/8954a831802d443b8da39f4122698d9c.png)
1.3:API:加权有向图
1.4:Java 实现:加权有向图
edu.princeton.cs.algs4.EdgeWeightedDigraph
![![image-20240315092205110]](https://img-blog.csdnimg.cn/direct/a85032c7817044d88d1ddd8425a0f49e.png)
![![image-20240315092241700]](https://img-blog.csdnimg.cn/direct/3f9a7e0f3ec84d979bbe9da97f4bcb0c.png)
1.5:API:最短路径
2:最短路径性质
2.1:最短路径的数据结构
目标: 找到从顶点 s 到其他所有顶点的最短路径。
观察结论: 存在一种最短路径树(Shortest Paths Tree, SPT)解法。为什么?
结果: 可以通过两个以顶点索引为键的数组来表示 SPT:
distTo[v]表示从顶点 s 到顶点 v 的最短路径长度。edgeTo[v]表示从顶点 s 到顶点 v 的最短路径上的最后一段边。
对应书本的介绍:
2.2:边的松弛 edge relaxation
对边 e = v → w 进行松弛操作时:
distTo[v]保存已知从源点 s 到顶点 v 的最短路径长度。distTo[w]保存已知从源点 s 到顶点 w 的最短路径长度。edgeTo[w]记录已知从源点 s 到顶点 w 的最短路径上最后经过的边。- 若通过边
e = v → w能够到达顶点 w,并且这条路径比之前已知的从 s 到 w 的最短路径更短,则更新distTo[w]以及edgeTo[w]。
2.3:最优性条件 optimality conditions
命题: 设G是一个带权有向图(edge-weighted digraph),则 distTo[] 数组存储的是从源点 s 到各顶点的最短路径距离,当且仅当满足以下条件:
distTo[s] = 0,即源点s到自身的最短路径距离为0。- 对于每个顶点 v,
distTo[v]表示从源点 s 到顶点 v 的某条路径的长度。 - 对于每条边
e = v → w,distTo[w]的值小于等于从源点 s 经由顶点 v 再到顶点 w 的路径长度,即distTo[w] ≤ distTo[v] + e.weight(),其中e.weight()表示边v → w的权重。
对应书本命题 P:
必要性证明:
对应书本的证明:
充分性证明:
对应书本的证明:
2.4:通用算法 generic shortest-paths algorithm
对应书本命题 Q:
3:Dijkstra 算法
3.1:demo 演示
- 按照离源点 s 的距离递增顺序考虑顶点(选取具有最低
distTo[]值的非树顶点)。 - 将该顶点添加至树结构中,并对其指向的所有边执行松弛操作。
初始状态:
距离 s 最近是顶点 0,从顶点 0 开始:
对从顶点 0 开始的边进行松弛操作:
顶点 0 到 1 为最短路径,继续选择顶点 1:
对从顶点 1 开始的边进行松弛操作:
顶点 0 到 7 为最短路径,继续选择顶点 7:
对从顶点 7 开始的边进行松弛操作:
顶点 0 到 4 为最短路径,继续选择顶点 4:
对从顶点 4 开始的边进行松弛操作:
顶点 4 到 5 为最短路径,继续选择顶点 5:
对从顶点 5 开始的边进行松弛操作:
顶点 5 到 2 为最短路径,继续选择顶点 2:
对从顶点 2 开始的边进行松弛操作:
顶点 2 到 3 为最短路径,继续选择顶点 3:
对从顶点 3 开始的边进行松弛操作:
顶点 2 到 6 为最短路径,继续选择顶点 6:
对从顶点 6 开始的边进行松弛操作:
s 开始的最短路径树:
3.2:证明
对应书本命题 R:
3.3:Java 实现
edu.princeton.cs.algs4.DijkstraSP
![![image-20240315115804455]](https://img-blog.csdnimg.cn/direct/f5515da674fc46e6a5824fe1f6db679b.png)
![![image-20240315115855899]](https://img-blog.csdnimg.cn/direct/ddcdab54a8464c999608ebb439f0fc4a.png)
edu.princeton.cs.algs4.DijkstraSP#relax
![![image-20240315120026331]](https://img-blog.csdnimg.cn/direct/458c0b7a9c2d4e6ca78a795470993146.png)
3.4:计算图生成树
Dijkstra 算法应该相当熟悉吧?
- Prim 算法在本质上是相同的算法。
- 两者都属于计算生成树的一类算法。
主要区别在于 选择下一个加入树中的顶点时所依据的规则:
- Prim 算法选择的是距离当前生成树最近的顶点(通过无向边);
- 而 Dijkstra 算法选择的是距离源点最近的顶点(通过有向路径)。
注: 深度优先搜索(DFS)和广度优先搜索(BFS)也属于这一类用于生成树或遍历图的算法。
3.5:运行时间
(同 Prim 算法)
核心要点:
- 采用数组实现对稠密图(Dense graphs)而言是最佳方案。
- 对于稀疏图(Sparse graphs),二叉堆在性能上要快得多。
- 在对性能要求极高的情况下,使用四路堆(4-way heap)是值得投入精力提升性能的。
- 斐波那契堆在理论上的优越性虽高,但在实际开发中却未必值得进行具体实现。
4:无环加权有向图 edge-weighted DAGs
4.1:demo 演示
- 按拓扑排序考虑顶点。
- 从该顶点出发对所有指向的边进行松弛操作。
初始状态:
首先对顶点进行拓扑排序:
从顶点 0 开始,对从顶点 0 开始的边进行松弛操作:
继续选择顶点 1,并进行松弛操作:
继续选择顶点 4,并进行松弛操作:
继续选择顶点 7,并进行松弛操作:
继续选择顶点 5,并进行松弛操作:
继续选择顶点 2,并进行松弛操作:
继续选择顶点 3,并进行松弛操作:
继续选择顶点 6,并进行松弛操作:
s 开始的最短路径树:
4.2:证明
对应书本命题 S:
4.3:Java 实现
edu.princeton.cs.algs4.AcyclicSP
![![image-20240316151408099]](https://img-blog.csdnimg.cn/direct/97f3d28dc3f04373b5b70dfa4a5dc92a.png)
![![image-20240316151431446]](https://img-blog.csdnimg.cn/direct/5bbd129d91e14d47ba2cad3afa914ba4.png)
4.4:最长路径
带权重有向无环图(DAG)中的最短路径问题:
- 对所有边的权重取反。
- 找出这些取反权重后的最短路径。
- 在得到的结果中再次对边的权重取反。
(等价于:在 relax() 函数中反转相等性判断的方向)
关键点: 拓扑排序算法即使在存在负权边的情况下也能正常工作。
5:负权重 negative weights
5.1:失败尝试
Dijkstra 算法: 该算法无法处理具有负权重的边。
重赋权重法: 对所有边权重增加一个常数值的方法无效。
结论: 我们需要采用一种不同的算法来解决此问题。
5.2:负权重环 negative cycles
对应书本定义以及命题 W:
5.3:Bellman-Ford 算法
对应书本命题 X:
5.3.1:demo 演示
重复 V 次:松弛有向图 E 所有边。
初始状态:
初始化,将到源的距离设置为 0:
对顶点 0 所有有向边进行松弛操作:
对顶点 1 所有有向边进行松弛操作:
对顶点 2 所有有向边进行松弛操作:
对顶点 3 所有有向边进行松弛操作:
对顶点 4 所有有向边进行松弛操作:
对顶点 5 所有有向边进行松弛操作:
对顶点 7 所有有向边进行松弛操作:
以上完成第一轮操作。
再次进行松弛操作。
大部分操作与第一轮类似,但也有可以更新的部分:
同理进行后续的循环:
没有更加优化的路径,完成所有松弛操作。
最终得到 s 开始的最短路径树:
5.3.2:算法分析
对应书本命题 Y:
5.4:成本开销小结
- 注释1: 存在有向循环会使问题求解难度增大。
- 注释2: 负权重边的存在会使问题变得更加复杂。
- 注释3: 负权重环会导致问题无法有效解决或无解状态。
6:小结
非负权重:
- 在许多应用中出现。
- Dijkstra 算法的时间复杂度接近线性时间。
无环带权有向图:
- 在某些应用中出现。
- 通过拓扑排序算法可以在线性时间内求解。
- 边的权重可以为负。
负权重和负权重环:
- 在某些应用中出现。
- 如果不存在负权重环,可以通过 Bellman-Ford 算法找到最短路径。
- 若存在负权重环,仍可通过 Bellman-Ford 算法找到一条路径(但可能不是最短路径)。
最短路径问题是广泛应用于问题求解的一个模型。
(完)
![![image-20240315082159395]](https://img-blog.csdnimg.cn/direct/71af863f96e84630a98565c4f63b729c.png)

![![L15-44ShortestPaths_04]](https://img-blog.csdnimg.cn/direct/14c2e051dd4f4550840fc73a40831276.png)
![![image-20240315085348075]](https://img-blog.csdnimg.cn/direct/abef7b3d9de94218b771642d46667db0.png)
![![image-20240315085915603]](https://img-blog.csdnimg.cn/direct/7ef5478d5be04ac18f9f494add25c9cd.png)
![![image-20240315090301981]](https://img-blog.csdnimg.cn/direct/29dd6a098e2f47939d82b558441bc167.png)
![![image-20240315090431816]](https://img-blog.csdnimg.cn/direct/4ce94dbc2548477dbe1ebc8250d60b63.png)
![![image-20240315092512628]](https://img-blog.csdnimg.cn/direct/ea9912577ead4e64967a8d5d70d19a05.png)
![![L15-44ShortestPaths_14]](https://img-blog.csdnimg.cn/direct/813dda20576840029f05073abd03cf2c.png)
![![image-20240315094302501]](https://img-blog.csdnimg.cn/direct/7fe845cd3e79492285b5593eaa01c52f.png)
![![image-20240315093903240]](https://img-blog.csdnimg.cn/direct/c6af2ffc4b444ccdaddd4718b408f7ff.png)
![![L15-44ShortestPaths_16]](https://img-blog.csdnimg.cn/direct/5e1a5752c3bd4c4c9ea76a011987deda.png)
![![image-20240315095849401]](https://img-blog.csdnimg.cn/direct/61fe0831cef64594a46958f4d3db3d15.png)
![![image-20240315100606867]](https://img-blog.csdnimg.cn/direct/67a4b4ac2b4147ccbe001cf915104614.png)
![![image-20240315100652432]](https://img-blog.csdnimg.cn/direct/612c7a543ddf443baa8842cd9e37c656.png)
![![image-20240315101018144]](https://img-blog.csdnimg.cn/direct/cd03fc98146f4283be754677e5f4c34f.png)
![![image-20240315101424511]](https://img-blog.csdnimg.cn/direct/c3209df5b320476ab35c147e09085bd5.png)
![![image-20240315101504323]](https://img-blog.csdnimg.cn/direct/b60232008db74928935ed260f8f18aa8.png)
![![image-20240315101559185]](https://img-blog.csdnimg.cn/direct/c059a76608ff400d864bc334f7ec0852.png)
![![image-20240315102227890]](https://img-blog.csdnimg.cn/direct/6f4afdcd61e4492ea66fcfddc72f10d2.png)
![![image-20240315103616581]](https://img-blog.csdnimg.cn/direct/02a12244a43549379f39d0f79d5e0dd7.png)
![![image-20240315103812262]](https://img-blog.csdnimg.cn/direct/4363ea2f444e4563a5736c6fa45e8945.png)
![![image-20240315103957761]](https://img-blog.csdnimg.cn/direct/814d3daf25cc4b9f912da9dbb946a179.png)
![![image-20240315104159042]](https://img-blog.csdnimg.cn/direct/b102a6854b3342389eb84caa6638d64c.png)
![![image-20240315110732282]](https://img-blog.csdnimg.cn/direct/39cc6b3da2fe4c059948df9cd209c70e.png)
![![image-20240315110937592]](https://img-blog.csdnimg.cn/direct/b942c55099bf4db885691608b135ea44.png)
![![image-20240315111120815]](https://img-blog.csdnimg.cn/direct/166091d9d4084966a19f4c48aafe29e9.png)
![![image-20240315112458304]](https://img-blog.csdnimg.cn/direct/48afdbed71fd407bbb57e862b6d03364.png)
![![image-20240315112525900]](https://img-blog.csdnimg.cn/direct/2293e4d15af64b9eb56090d57b0e2bbb.png)
![![image-20240315112605879]](https://img-blog.csdnimg.cn/direct/ab9c918b1fd0408ca73694ac02f04881.png)
![![image-20240315112740572]](https://img-blog.csdnimg.cn/direct/5642241bd25b47babff03f0d7bf17ca7.png)
![![image-20240315112842144]](https://img-blog.csdnimg.cn/direct/6b96be4cafef46bcadb29b185b94669d.png)
![![image-20240315112904984]](https://img-blog.csdnimg.cn/direct/15b4d73b69ed44a498cb9e000d427642.png)
![![image-20240315113029552]](https://img-blog.csdnimg.cn/direct/78e4009f61944e0cbee4c3ba5b0e9f94.png)
![![image-20240315113110077]](https://img-blog.csdnimg.cn/direct/0608256ed0214ca2849ba8ff6cfd77d6.png)
![![image-20240315113126024]](https://img-blog.csdnimg.cn/direct/5cd4470dae2a4b9d9400da8ef6c8047e.png)
![![image-20240315113207365]](https://img-blog.csdnimg.cn/direct/0c4c5364a58e43f3849dc49890c0b9bb.png)
![![image-20240315113236950]](https://img-blog.csdnimg.cn/direct/1097b5019a5144d9973d97f8cc83bf33.png)
![![image-20240315113249721]](https://img-blog.csdnimg.cn/direct/bcdbda6aee1c470eb720233b63807481.png)
![![image-20240315113329032]](https://img-blog.csdnimg.cn/direct/e46813ec513e44d2bfe08ac31316e36b.png)
![![image-20240315113348502]](https://img-blog.csdnimg.cn/direct/4b6dd50881674645ac865f18bf25672b.png)
![![image-20240315113406022]](https://img-blog.csdnimg.cn/direct/1415af10fbf74b2ca9dadab040fdcc28.png)
![![image-20240315113446235]](https://img-blog.csdnimg.cn/direct/5738541f977e47c08e9d386c742d65c2.png)
![![image-20240315113534275]](https://img-blog.csdnimg.cn/direct/3b12edf2ccda44888870f5c1f72145ec.png)
![![image-20240315113948791]](https://img-blog.csdnimg.cn/direct/79d428dbf0c74dcfbaabd5c05af47992.png)
![![L15-44ShortestPaths_29]](https://img-blog.csdnimg.cn/direct/8473fb330d17487e8e288a635ea38417.png)
![![image-20240315114148251]](https://img-blog.csdnimg.cn/direct/4038387ce98b416f8c8241e05976047d.png)
![![L15-44ShortestPaths_33]](https://img-blog.csdnimg.cn/direct/2bb4123065b644a896612dc4f7320510.png)
![![L15-44ShortestPaths_32]](https://img-blog.csdnimg.cn/direct/198bc1999dcc40ef888a109df417334f.png)
![![image-20240316134718054]](https://img-blog.csdnimg.cn/direct/50a6e799c8f7419a97cda1e61356ff24.png)
![![image-20240316134854048]](https://img-blog.csdnimg.cn/direct/a4781aadb2a5403f8793c0152a4f3a16.png)
![![image-20240316135043894]](https://img-blog.csdnimg.cn/direct/8e033cb288744dc792c53849491dab94.png)
![![image-20240316135324509]](https://img-blog.csdnimg.cn/direct/17cefad7da10455a97908ce9e5b4a5b4.png)
![![image-20240316135515915]](https://img-blog.csdnimg.cn/direct/0565bbdd64064bd38ce857d22b7a51b6.png)
![![image-20240316141338821]](https://img-blog.csdnimg.cn/direct/dffea7266da54569893164eca2db74dc.png)
![![image-20240316141608117]](https://img-blog.csdnimg.cn/direct/d7714b04b3a045ff91c9f08c9ddb4bd9.png)
![![image-20240316141644511]](https://img-blog.csdnimg.cn/direct/f5d3c690ce424795ba7c6deb5eb814aa.png)
![![image-20240316141819644]](https://img-blog.csdnimg.cn/direct/fe1d957d5c954fcfacd35449177fe2a3.png)
![![image-20240316143812156]](https://img-blog.csdnimg.cn/direct/86213373ff414fecb389816bdf52f338.png)
![![image-20240316143839873]](https://img-blog.csdnimg.cn/direct/179f0fc58c67484a81a72142a5117635.png)
![![image-20240316144501557]](https://img-blog.csdnimg.cn/direct/2c75c90a698942dbb1033a7bb8cfca47.png)
![![L15-44ShortestPaths_38]](https://img-blog.csdnimg.cn/direct/0e7ea39cc86945fbbe75f9603ef2cac4.png)
![![image-20240316145708486]](https://img-blog.csdnimg.cn/direct/4820138f06ad4c08b6fbd30fb4aa8c29.png)
![![L15-44ShortestPaths_46]](https://img-blog.csdnimg.cn/direct/33184a2e5a374cf99b40c19fb77c18f8.png)
![![L15-44ShortestPaths_51]](https://img-blog.csdnimg.cn/direct/3c0cd0f677884062b9932d8d7b18b36d.png)
![![L15-44ShortestPaths_52]](https://img-blog.csdnimg.cn/direct/118b29641e664bb6a1910ecf0af5620f.png)
![![image-20240316161032461]](https://img-blog.csdnimg.cn/direct/68fa7882ac854b4184b7529cebe39991.png)
![![image-20240316161058157]](https://img-blog.csdnimg.cn/direct/70aedc6b38064bdba5e468b086d406fa.png)
![![L15-44ShortestPaths_53]](https://img-blog.csdnimg.cn/direct/84ae007c78ce422c926381b71479450d.png)
![![image-20240316163337743]](https://img-blog.csdnimg.cn/direct/fe819d7a1c404c7ba73660820506a1bd.png)
![![image-20240316163457806]](https://img-blog.csdnimg.cn/direct/d2858e92b8c04a72821923c7c06754d1.png)
![![image-20240316163628062]](https://img-blog.csdnimg.cn/direct/179f918f96f845e89ea58c41160d1bbe.png)
![![image-20240316163838365]](https://img-blog.csdnimg.cn/direct/6df1e884728f4a019c094f81cd01ec5e.png)
![![image-20240316164534404]](https://img-blog.csdnimg.cn/direct/ce2483b6c01f45a79a2e0a099fafc417.png)
![![image-20240316164759986]](https://img-blog.csdnimg.cn/direct/7d817deac2474dd5aa28047db515ef79.png)
![![image-20240316164813178]](https://img-blog.csdnimg.cn/direct/4d4b7ab3312e43ad823e9555780305d8.png)
![![image-20240316164925311]](https://img-blog.csdnimg.cn/direct/1449d97e2b33468da66448daa2f381ec.png)
![![image-20240316164943422]](https://img-blog.csdnimg.cn/direct/3514f34c52c14953bdf112812154918e.png)
![![image-20240316165014037]](https://img-blog.csdnimg.cn/direct/31bd8432363c40d09a247c879952c7fb.png)
![![image-20240316165052683]](https://img-blog.csdnimg.cn/direct/dfed563ac53a4a898a8ce3da829a6573.png)
![![image-20240316165128407]](https://img-blog.csdnimg.cn/direct/0a3f1923cf5542d0b2fc43bdd97254b4.png)
![![image-20240316165152695]](https://img-blog.csdnimg.cn/direct/0c3a28445b1e439e86f45732664cec80.png)
![![image-20240316165252427]](https://img-blog.csdnimg.cn/direct/9e53da1be51644d98ed06a9d12aa1988.png)
![![image-20240316165320702]](https://img-blog.csdnimg.cn/direct/238eaae8405b45bf842d5017d4d5bd6b.png)
![![image-20240316165349289]](https://img-blog.csdnimg.cn/direct/f109a669b5dd49be84934c2957d244d1.png)
![![image-20240316165439474]](https://img-blog.csdnimg.cn/direct/b0654da51036476bbec39ac86e8baf1f.png)
![![image-20240316165504694]](https://img-blog.csdnimg.cn/direct/a74dc9303f0744f5ad0e4b05a831bdd6.png)
![![image-20240316165531693]](https://img-blog.csdnimg.cn/direct/c5ee07377a064e3cbcbb3c972b1b40ae.png)
![![image-20240316165552335]](https://img-blog.csdnimg.cn/direct/48e0bc7a8d1949cdbb8fc43536b0481e.png)
![![image-20240316165907917]](https://img-blog.csdnimg.cn/direct/c7e824b9056649e582b634fd05fb4496.png)
![![image-20240316170050428]](https://img-blog.csdnimg.cn/direct/c72e46b814b948909967fab2b3f6e9c9.png)
![![image-20240316170146032]](https://img-blog.csdnimg.cn/direct/7d94ff75e645408ea103333902799df8.png)
![![image-20240316170308062]](https://img-blog.csdnimg.cn/direct/51f8fd001d824785865782d5937dd0c5.png)
![![L15-44ShortestPaths_57]](https://img-blog.csdnimg.cn/direct/7c784759410d4740a8f252deb2a3276d.png)
![![image-20240316181217238]](https://img-blog.csdnimg.cn/direct/b5ca824a05d14347a334cb8bb8bb0109.png)
![![L15-44ShortestPaths_59]](https://img-blog.csdnimg.cn/direct/beb6d1beeee6476da146739bb8db15bf.png)
![![L15-44ShortestPaths_65]](https://img-blog.csdnimg.cn/direct/818fced60a9d4098bffb256a99584e88.png)
![![image-20240316183053632]](https://img-blog.csdnimg.cn/direct/303bebeca469466ab56969244a031bc6.png)



![[RAM] RAM 突发传输(Burst ,Burst size, length) | Burst 读写过程与时序 精讲](https://img-blog.csdnimg.cn/direct/fb683d54959448ff83e1cd1c1b34a757.png)