题目

有 n个小朋友坐成一圈，每人有 a[i]个糖果。

每人只能给左右两人传递糖果。

每人每次传递一个糖果代价为 1。

求使所有人获得均等糖果的最小代价。

输入格式

第一行输入一个正整数 n，表示小朋友的个数。

接下来 n 行，每行一个整数 a[i]，表示第 i 个小朋友初始得到的糖果的颗数。

输出格式

输出一个整数，表示最小代价。

数据范围

1≤n≤1000000,
0≤a[i]≤2×10的9次方,
数据保证一定有解。

输入样例：

4
1
2
5
4

输出样例：

4

思路

1. 糖果不会凭空增加或者消失；本题只考虑一定有解的情况，也就是总数一定能够整除n；不会出现环形给的情况：a->b->c->a;
2. 数据范围是1e6,所以要做到nlogn或者是O(n)的情况;
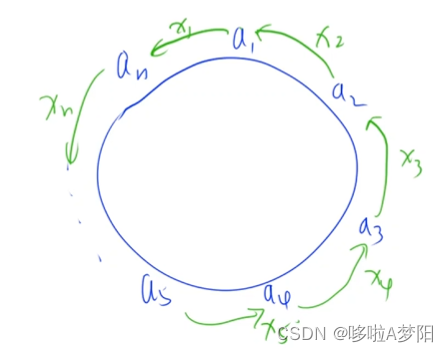
3. 建立数学模型：
   1. xi可正可负；
   2. 目标：使所有xi的绝对值相加之和最小
   3. 限制：

      

   4. n-1个独立的方程，n个未知数，可以用某一个的x来表示其他的x
      
   5. 目标函数转化为：（类似上一题的货物运输：求中位数+求Ci）
      
   6. 

代码

n = int(input())
a=[int(input()) for _ in range(n)]
# print(l1)
c=[0 for _ in range(n)]
avg=sum(a)//n
for i in range(n-1,0,-1):
    c[i-1] = c[i]+avg-a[i] 
    # 注意下标范围是从0开始的，题解下标从1开始
c.sort()
res=0
for i in range(n):
    res+=abs(c[i]-c[(n-1)//2])
print(res)