一维插值是指对一维函数进行插值。已知n+1个结点(x,y,),其中x,互不相同(j=0,1,2,... n),求任意插值点x*处的插值y*。
求解一维插值问题的主要思想是:设结点由未知的函数g(x)产生,函数g(x)为连续函数且g(x)=y;(j=0,1,...,n);接着构造相对简单的且容易实现的函数f(x)来逼近函数g(x),使f(x)可以经过n+1个结点,即f(x)=y;(j=0,1,2,,n), 接着使用函数f(x)计算插值点x*处的插值,即y* =f(x*)。
在MATLAB中,使用interp1函数可以实现一维插值,该函数是利用多项式插值函数,将被插值的函数近似为一个多项式函数,其调用格式如下。
yi= interpl(x,y ,xi, method) %对数据向量x和y依次选用合适的方法进行插值函数的构造,并计算xi
%处的函数值,返回给yi, “method"为指定的插值方法。其中,x必须是矩
%阵,y既可以是向量也可以是矩阵。若y是向量,则长度必须与x相同,
%此时xi可以是标量、向量或任意维矩阵,yi与xi大小相同;若y是矩阵, %则其大小必须是[ n,d1 ,d2,.",dk],n为向量x的长度,函数对d1 *d2*
%...*dk组y值都进行插值
yi= interpl(x,y ,xi,method, 'extrap ' ) % 对数据向量x和y依次选用合适的方法进行插值函数的构
%造,并计算xi处的函数值,返回给yi,"method"为指定的插值
%方法,并对超出数据范围的插值数据指定外推方法
yi= interpl(x,y ,xi,method, extrapval) % 对数据向量x和y依次选用合适的方法进行插值函数的构
%造,并计算xi处的函数值,返回给yi," method"为指定的插 %值方法,并对超出数据范围的插值数据返回extrapval 值,一 %般设为NaN或者0
yi=iterp1(x,y,xi,'pp ') %对数据向量 x和y依次选用合适的方法进行插值函数的构造,并计算xi
%处的函数值,返回给yi,"method"为指定的插值方法,返回值pp为数据y
%的分段多项式形式
yi= interpl(y,xi) %ox 和method均为默认设置,即x=1:N,其中N=size( Y); method= linear
%此外,若数据点是不等间距分布式,则interplq函数比interp1函数执行的速度快,
%因为前者是不检查已知数据点是否等间距,但inteplq函数要求x必须是单调递增的
在一维插值方法中,具有多种不同的指定插值方法,每种插值方法在速度、平滑性、内存使用方面都是有所不同的,下面将对“method”中这些指定的插值方法进行介绍。
1)最邻近插值法( nearest): 在已知数据的最邻近点设置插值点,对插值点的数进行四舍五人,对超出范围的点将返回NaN。该插值方法速度最快,但结果的平滑性差。
2)线性插值法(linear): 对未指定插值方法时所采用的方法。直接连接相邻的两点,对超出范围的点将返回NaN,占用的内存比最邻近插值法多,运行时间略长,生成的结果是连续的且在顶点处存在坡度变化。
3)三次样条插值(spline):使用三次样条丽数获取插值点。在已知点为端点的情况下,插值函数至少具有相同的一阶和二阶导数,为非常有用的插值方法。该方法处理速度最慢,占用内存小于分段三次厄米多项式插值,产生最光滑的结果,但当输人的数据分布不均匀或数据点间距过近时将产生错误。
4)三次插值( eubic):该参数取值的特点可参考帮助文档,需要更多内存,运行时间比最邻近法和线性插值要长;需要插值数据及其导数都是连续的。
5)三次多项式插值( v5eubic):该参数取值的特点可参考帮助文档,相比线性插值,其处理速度慢、内存消耗较多,使用三次多项式函数对已知数据进行拟合。
6)分段三次厄米多项式插值(pchip): 该参数取值的特点可参考帮助文档,在处理速度和内存消耗方面比线性插值差,插值得到的数据和--阶导数是连续的。
在MATALAB中常用的4种插值方法分别是最邻近插值法.线性插值法、三次样条插值法和三次插值法,其特点见表。

通常,插值运算分为以下两种。
1)内插值是指只对已知数据点集内部的点进行插值。该插值方法可以根据已知的数据点分布,构建可以代表分布特性的函数关系,可以较为准确地估计插值点上的函数值。
2)外插值是指对已知数据点集外部的点进行插值。想要较为准确地估计外插丽数值是很难的。
例:使用不同的方法对cos函数进行插值。
输人以下代码,生成的结果如图所示。
>>x=0:10;
y=cos(x);
xi=0:.25:10;
yi= interp1(x,y,xi);
subplot(221);
plot(x,y,'o',xi,yi);
xlabel( '(a)linear插值算法');
yi = interp1(x,y,xi, nearest ');
subplo(222);
plot(x,y,'o' ,xi,yi);
xlabel('(b) nearest插值算法');
yi= interp1(x,y,xi, ' v5cubic ');
subplot(223) ;
plot(x,y,'o',xi,yi);
xlabel('(c) v5cubic插值算法');
yi= interp1(x,y,xi, ' spline ');
subplot( 224) ;
plot(x,y,'o',xi,yi);
xlabel( '(d) spline插值算法');

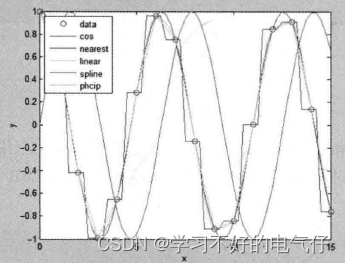
例:外插运算的方法。
输人以下代码,生成的结果如图所示。
x=0:15;
y=cos(x);
xi=0:.25:15;
yi=sin(xi);
y1=interp1(x,y,xi,'nearest','extrap');
y2=interpl(x,y,xi,'linear','extrap');
y3=interp1(x,y,xi,'spline','extrap');
y4=interp1(x,y,xi,'vScubic','extrap');
y4=interpl(x,y,xi,'pchip','extrap');
plot(x,y,'o',xi,yi,xi,yl,xi,y2,xi,y3,xi,y4);
legend('data','cos','nearest','linear','spline','pheip',2);
xlabel('x');
ylabel('y');