算法复杂度中大O的含义
推荐教程:北大硕士带你手撕Leetcode算法题
大O复杂度表示法
算法面试中, 经常会被问到,你写的算法复杂度是多少, 或者设计一个复杂度为 O(nlogn) 的算法复杂度分析是估算算法执行效率的方法,公式O(f(n))表示算法的复杂度,此方法即为大O复杂度表示法O(f(n))中n表示数据规模,f(n)表示运行算法所需要执行的指令数。
下面的代码非常简单,求 1,2,3…n 的累加和,我们来估算它的执行效率

假设每行代码执行的时间都一样为t:
•执行第2行代码需要时间t,第3,4行代码运行了n遍,需要的时间为2n*t
•这段代码总执行时间为(2n+1)* t
结论:代码执行的总时间T(n)与每行代码的执行次数成正比
看下面的代码,估算该段代码的执行时间

同样假设每行代码执行的时间都一样为t:
•执行第2行代码需要时间t
•第3行代码运行了n遍,需要时间为n*t
•第4、5行代码运行了n2次,需要时间为2n2 * t
•执行所有代码的总时间为 (2n2 + n + 1)* t
结论:代码执行的总时间T(n)与每行代码的执行次数成正比
用O(f(n))来表示算法复杂度

T(n) = O(f(n)) , O表示代码的执行时间T(n) 与 f(n)表达式成比例。
大O复杂度表示法:上面例子中的T(n) = O(2n+1), 另一个 T(n) = O(2n2 + n + 1)。
大O时间复杂度并不表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,也叫作渐进时间复杂度
(asymptotic time complexity),简称时间复杂度
当数据量特别大, 也就是n的取值很大的时候,大O表示法中低阶、常量、系数三部分并不会左右增长趋势,可以忽略

上面例子中的T(n) = O(2n+1), 另一个 T(n) = O(2n2 + n + 1)
用大O表示法表示上面两段代码的时间复杂度,可以记为O(n),O(n2)

数据规模
通过下面的例子,我们来体会一下数据规模对程序运行时间的影响

通过刚才的例子我们可以得出如下结论,如果想在1s之内解决问题
O(n2) 的算法可以处理大约104级别的数据
O(n) 的算法可以处理大约108 级别的数据
O(nlogn)的算法可以处理大约107级别的数据
有的时候,自己写的算法认为是O(nlogn), 但是在线判题系统提示超时,可以先估计一下,前面提到标准降低一个数量级
O(n2) 的算法可以处理大约103级别的数据
O(n) 的算法可以处理大约107 级别的数据
O(nlogn)的算法可以处理大约106级别的数据
自己写代码实验,数据每增加一个数量级看看耗时的变化
空间复杂度
解决问题时,多创建了一个数组:O(n)
解决问题时,多创建了一个二维数组:O(n2)
解决问题时,用到了几个临时的变量:O(1)

时间复杂度分析
如何分析一段代码的时间复杂度?
1.在分析一个算法、一段代码的时间复杂度时,只关注循环执行次数最多的那一段代码就可以了

上面的代码中,我们只需要关注内层for循环的时间复杂度就可以了
内层for循环的两行代码被执行了n2次,所以总的时间复杂度就是O(n2)
2.总复杂度等于量级最大的那段代码的复杂度

上面的代码分为两部分,分别是求 sum_、sum_1
计算sum_部分的代码段时间复杂度O(n),计算sum_1部分的代码段时间复杂度为O(n2)
总的时间复杂度由复杂度最大的部分决定, 所以上面代码复杂度为O(n2)
3.嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

上面的代码中第二个函数调用了第一个函数, 如果把fn函数调用当作一个普通操作, 那么第二个函数的时间复杂度为O(n)
Fn函数的时间复杂度为O(n),那么函数整体的时间复杂度为O(n*n) = O(n2)
4. 当两段代码的数据规模不同时,不能省略复杂度低的部分

上面的代码分为两部分,分别是求 sum_、sum_1
计算sum_部分的代码段时间复杂度O(n),计算sum_1部分的代码段时间复杂度为O(m2)
总的时间复杂度由复杂度最大的部分决定, 所以上面代码复杂度为O(m2+n)
需要注意的地方:
看见双重for循环,算法的复杂度一定是O(n2)么?

关于O(logn)
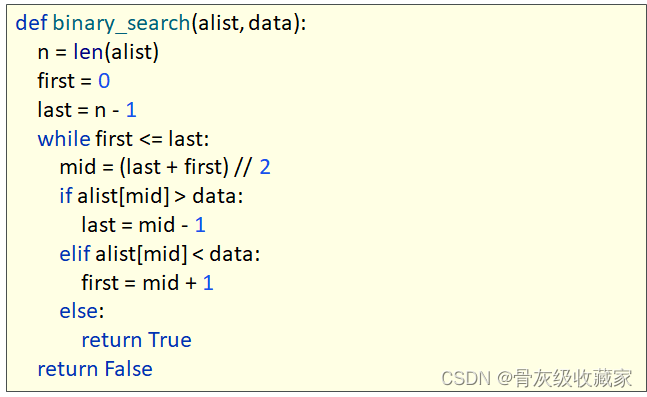
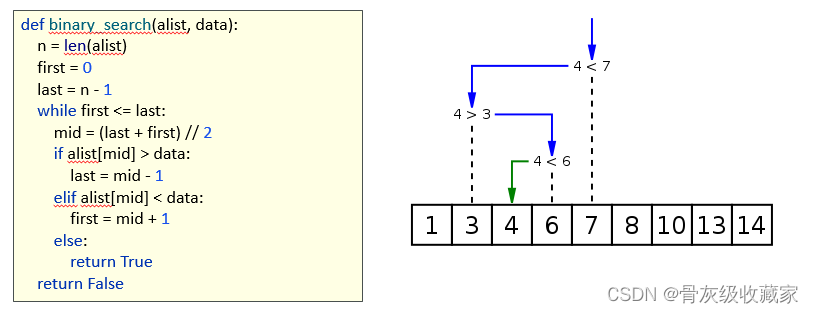
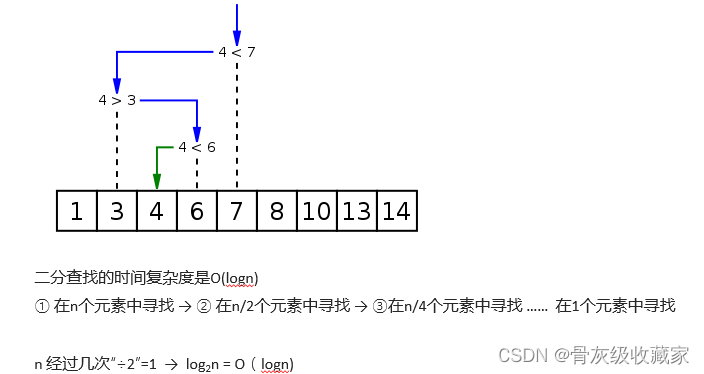

上面代码的时间复杂度 O(logn)
n 经过几次“÷10”=0 → log10n = O(logn)
关于O(logn)
logaN logbN 之间是什么关系?
logaN = logab * logbN
上面式子当中,logab 为常数,可以忽略
下面代码的复杂度:O(n2)

简单复杂度分析:
① 关注循环执行次数最多的那一段代码
② 总复杂度等于量级最大的那段代码的复杂度
③ 嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
④ 当两段代码的数据规模不同时,不能省略复杂度低的部分
⑤ 复杂度中对数的部分通常忽略底数
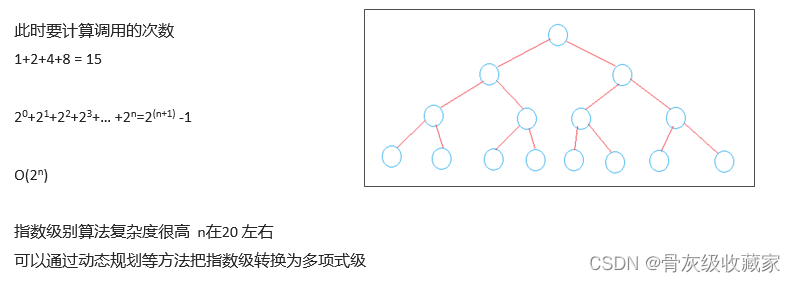
递归算法复杂度分析
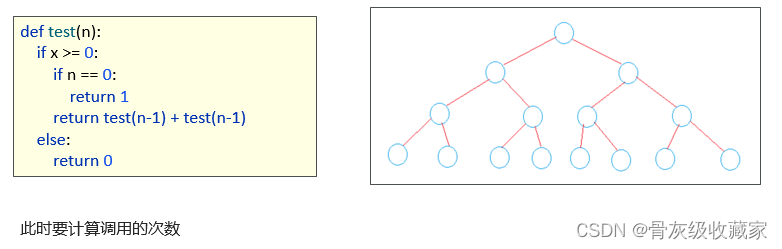
在递归中只做了一次递归调用时间复杂度:O(logn)

在递归中只做了一次递归调用
递归深度为D
在每个递归函数中, 时间复杂度为T
总体时间复杂度为O(T*D)


最好、最坏、平均时间复杂度分析
算法复杂度在有些情况下是用例相关的
插入排序算法O(n2) 最好情况:O(n)
快速排序算法O(nlogn) 最差情况:O(n2)
算法面试复杂度分析一般指的就是平均情况
均摊复杂度分析
某些复杂耗时操作是为了辅助其它操作,可以将这个复杂操作的时间平摊到其它操作中

每一次添加耗时O(1), 初始长度填满之后,再添加1个元素,此时需要开辟一块长度为2n的新的空间,并将之前的N个元素复制过来,这一步的操作复杂度为n,平均来看 O(2)
均摊复杂度:就是把过程复杂操作所耗费时间分担到简单操作上
对一个数据结构进行一组连续操作,大部分情况下时间复杂度都很低,只有个别情况下时间复杂度比较高,而且这些操作之间存在前后连贯的时序关系,这个时候,适合运用均摊复杂度分析代码