问题:从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径——最短路径。在博客动态规划算法中介绍了动态规划的基本思想已经建立动态规划模型的步骤,下面将其中的方法分析最短路径问题。
最短路径有一个重要特性:
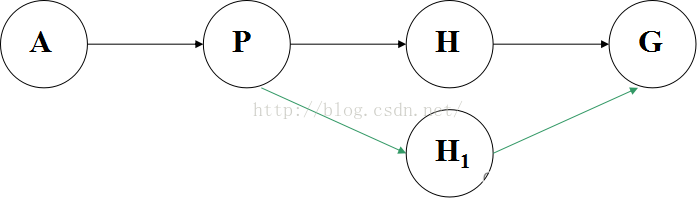
如果由起点A经过P点和H点而到达终点G是一条最短路线,则由点P出发经过H点到达终点G的这条子路线,对于从点P出发到达终点的所有可能选择的不同路线来说,必定也是最短路线。如下图:
例题分析:求从A到G的最短路径。
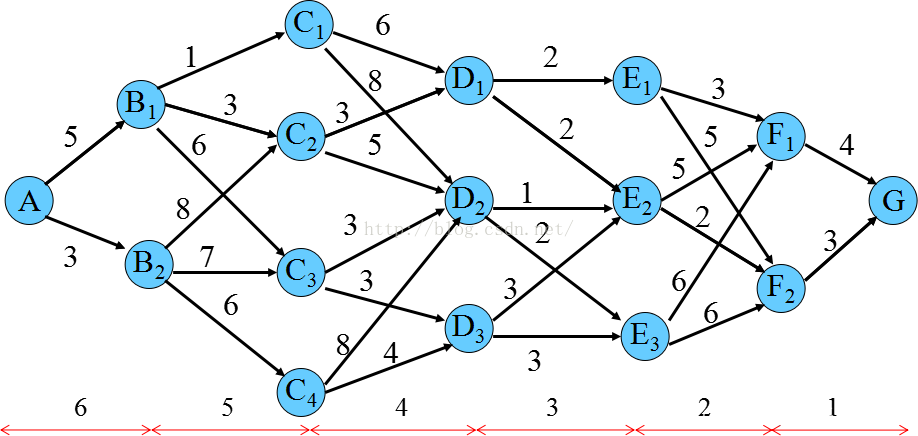
如上图,采用反向阶段编号,采用反向递推,状态为各阶段初始位置,目标函数:

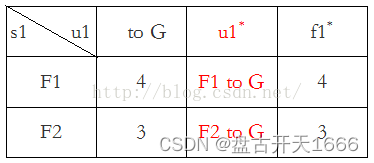
第一阶段:k = 1,s1有F1、F2两种可能状态,最优决策表如下
目标函数:

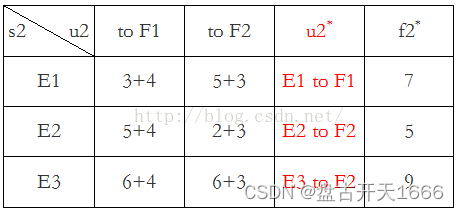
第二阶段:k = 2,s2有E1、E2、E3三种可能状态,最优决策表如下
目标函数:
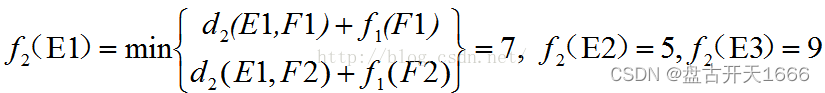
第三阶段:k = 3,s3有D1、D2、D3三种可能状态,最优决策表如下
目标函数:
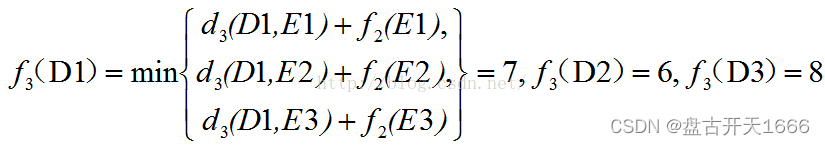
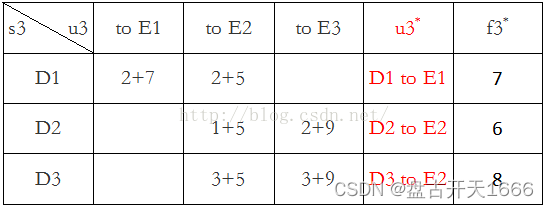
第四阶段:k = 4,s4有C1、C2、C3、C4四种可能状态,最优决策表如下
目标函数:
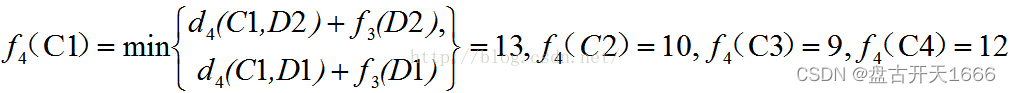
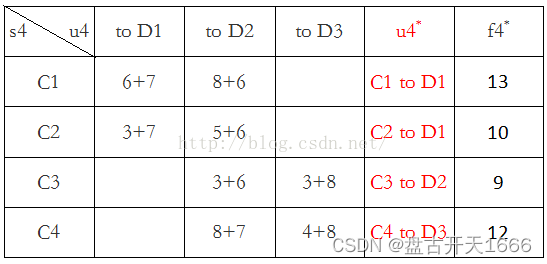
第五阶段:k = 5,s5有B1、B2两种可能状态,最优决策表如下
目标函数:
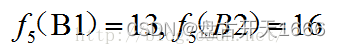
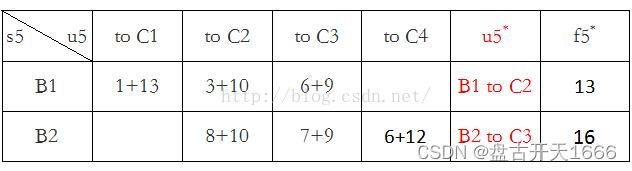
第六阶段:k = 6,s6有一种状态,最优决策表如下
目标函数:

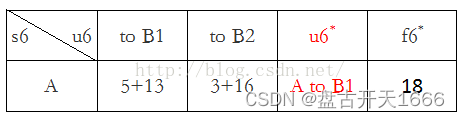
最短路径长度:18,最优策略:
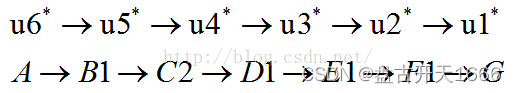
上面只是提供一种求解最短路径问题的方法,后续我还会编程实现最短路径问题的求解。