机器学习-04-分类算法-02贝叶斯算法

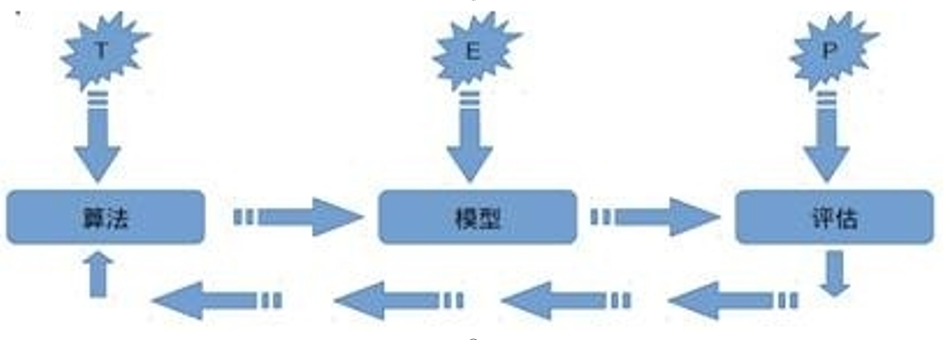
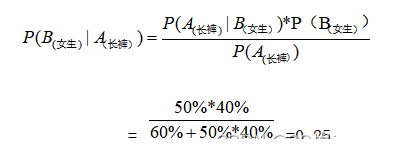总结

本系列是机器学习课程的系列课程，主要介绍机器学习中分类算法，本篇为分类算法与贝叶斯算法部分。

本门课程的目标

完成一个特定行业的算法应用全过程：

懂业务+会选择合适的算法+数据处理+算法训练+算法调优+算法融合
+算法评估+持续调优+工程化接口实现

参考

机器学习最易懂之贝叶斯模型详解与python实现

机器学习之朴素贝叶斯算法原理+Python实现

图解机器学习 | 朴素贝叶斯算法详解

图解机器学习算法：从入门到精通系列教程

简单，却又反直觉的“三门问题”，暴露出很多人根本不懂“概率”

大数据中的统计学基础——Day3

机器学习定义

关于机器学习的定义，Tom Michael Mitchell的这段话被广泛引用：
对于某类任务T和性能度量P，如果一个计算机程序在T上其性能P随着经验E而自我完善，那么我们称这个计算机程序从经验E中学习。

贝叶斯算法

预备知识

先验概率、条件概率、后验概率

条件概率: 就是事件A在事件B发生的条件下发生的概率，表示为P(A∣B)，读作“在B发生的条件下A发生的概率。

先验概率: 在贝叶斯统计中，某一不确定量 p的先验概率分布是指：在考虑"观测数据"前，也就是没有样本集的情况下，能表达 p不确定性的概率分布。先验概率是指根据以往的经验和分析得到的概率，往往作为“由因求果”问题中的“因”出现。

后验概率: 在贝叶斯统计中，一个随机事件或者一个不确定事件的后验概率是在考虑和给出相关证据或数据后所得到的条件概率。同样，后验概率分布是一个未知量（视为随机变量）基于试验和调查后得到的概率分布。“后验”在本文中代表考虑了被测试事件的相关证据。

现有两个随机变量A,B，其中A表示西瓜的颜色，B表示西瓜的好坏：

条件概率：
在瓜颜色是青绿的情况下，瓜是好瓜的概率，记为 P(B=好瓜∣A=青绿)；
在瓜是好瓜的情况下，瓜的颜色是青绿色的概率，记为P(A=青绿∣B=好瓜)。

先验概率：
瓜的颜色是青绿的概率，即 P(A=青绿)，称作是A的先验概率，因为它不用考虑任何B方面的因素；
瓜是好瓜的概率，即P(B=好瓜)，称作是B的先验概率，因为它不用考虑任何A方面的因素。

后验概率:

P(A=青绿∣B=好瓜)是在瓜是好瓜的情况下，瓜的颜色是青绿色的概率，也是由于得知B的取值后知道A的概率，所以是 A的先验概率；
P(B=好瓜∣A=青绿)是在瓜颜色是青绿的情况下，瓜是好瓜的概率，也是由于得知 A的取值后知道 B 的概率，所以是 B的先验概率

贝叶斯公式

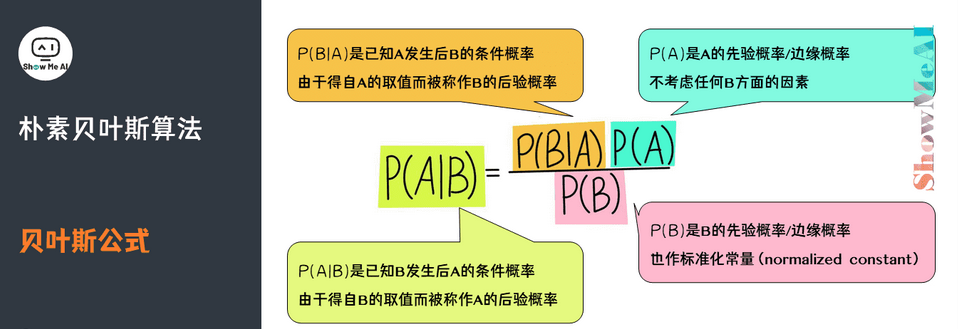
在这里插入图片描述

先验概率，在贝叶斯的很多应用中不重要（因为只要最大后验不求绝对值），需要时往往用全概率公式计算得到。P(A)叫做A事件的先验概率，即一般情况下，认为A发生的概率。
条件概率，又叫似然概率，一般是通过历史数据统计得到。P(B|A)叫做似然度，是A假设条件成立的情况下发生B的概率。
后验概率，一般是我们求解的目标。P(A|B)叫做后验概率，在B发生的情况下发生A的概率，也就是要求的概率。P(B)叫做标准化常量，即在一般情况下，认为B发生的概率。

贝叶斯定理（Bayes Theorem，也称贝叶斯公式）是基于假设的先验概率、给定假设下观察到不同数据的概率，提供了一种计算后验概率的方法。

穿裙子的概率

在这里插入图片描述
求： P(女生|长裤)—穿长裤人数中是女生的概率？

要知道穿长裤的人是女生的概率，要知道穿长裤女生的人数，也要知道穿长裤的总人数，两者相除就是长裤中女生的概率。假设学校人数为U

穿长裤总人数 = 穿长裤的男生人数+穿长裤的女生人数
= 60% * U + 40% * U *50%

穿长裤女生的人数 = 40% * U * 50%

随机抽取一个穿长裤的学生是女生的概率
= 穿长裤女生的人数/穿长裤总人数
= 40% * U * 50% / ( 60% * U + 40% * U *50%)
= 0.25

假设学生穿长裤记作事件A，学生穿长裤的概率就是P(A)。学生是女生记作事件B，学生是女生的概率是P(B)，求:抽取的这个穿长裤学生是女生的概率（P(B|A)）？

抽奖活动

某公司年终决定丼行抽奖活动，从全部员工中选取一名特等奖。公司人事架构如下：
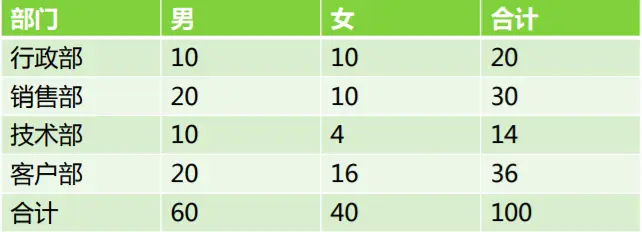
在这里插入图片描述

（1）若被抽中的人是销售部的，问该员工是女性的概率？
（2）若被抽中的人是女生的，问该员工是销售部的概率是？
解题上来要设事件！！

解：设A={被抽中的是销售部的}，B={被抽中的是女生}

(1)P(B|A)=P(AB)/P(A)=(10/100)/(30/100)=1/3

(2)P(A|B)=P(AB)/P(B)=(10/100)/(40/100)=1/4

病树浇水问题

病树的主人外出,委托邻居浇水,设已知如果不浇水,树死去的概率为0.8.若浇水则树死去的概率为0.15.有0.9的把握确定邻居会记得浇水.

(1)求主人回来树还活着的概率.

(2)若主任回来树还活着，求邻居忘了浇水的概率.

在这里插入图片描述

p=(0.10.8)/（0.10.8+0.9*0.15）=0.372

朴素贝叶斯算法核心思想

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素贝叶斯（Naive Bayes）分类是贝叶斯分类中最简单，也是常见的一种分类方法。
在这里插入图片描述

一般挑西瓜时通常要「敲一敲」，听听声音，是清脆声、浊响声、还是沉闷声。所以，我们先简单点考虑这个问题，只用敲击的声音来辨别西瓜的好坏。根据经验，敲击声「清脆」说明西瓜还不够熟，敲击声「沉闷」说明西瓜成熟度好，更甜更好吃。
在这里插入图片描述

所以，坏西瓜的敲击声是「清脆」的概率更大，好西瓜的敲击声是「沉闷」的概率更大。当然这并不绝对——我们千挑万选地「沉闷」瓜也可能并没熟，这就是噪声了。当然，在实际生活中，除了敲击声，我们还有其他可能特征来帮助判断，例如色泽、跟蒂、品类等。

朴素贝叶斯把类似「敲击声」这样的特征概率化，构成一个「西瓜的品质向量」以及对应的「好瓜/坏瓜标签」，训练出一个标准的「基于统计概率的好坏瓜模型」，这些模型都是各个特征概率构成的。

这样，在面对未知品质的西瓜时，我们迅速获取了特征，分别输入「好瓜模型」和「坏瓜模型」，得到两个概率值。如果「坏瓜模型」输出的概率值大一些，那这个瓜很有可能就是个坏瓜。

条件独立假设与朴素贝叶斯

于贝叶斯定理的贝叶斯模型是一类简单常用的分类算法。在「假设待分类项的各个属性相互独立」的情况下，构造出来的分类算法就称为朴素的，即朴素贝叶斯算法。

所谓「朴素」，是假定所有输入事件之间是相互独立。进行这个假设是因为独立事件间的概率计算更简单。

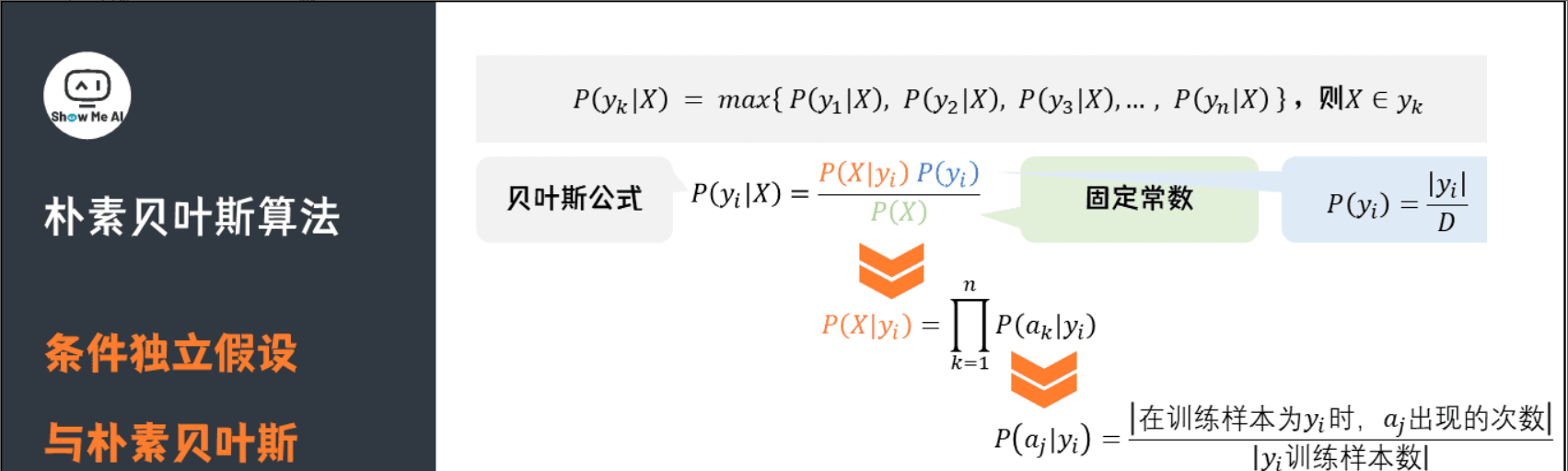
朴素贝叶斯模型的基本思想：对于给定的待分类项
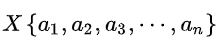
在这里插入图片描述

，求解在此项出现的条件下各个类别 yi 出现的概率，哪个 P(yi,X) 最大，就把此待分类项归属于哪个类别。

朴素贝叶斯算法的定义：设
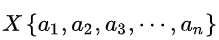
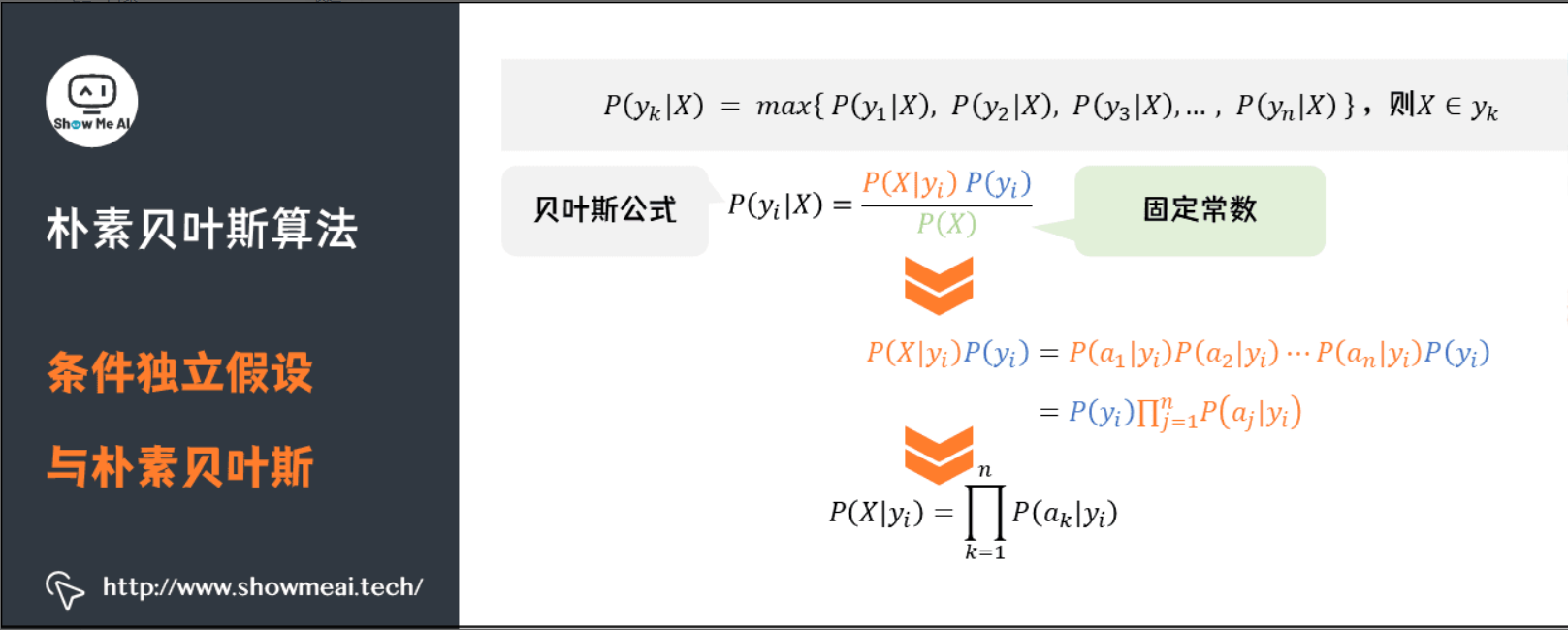
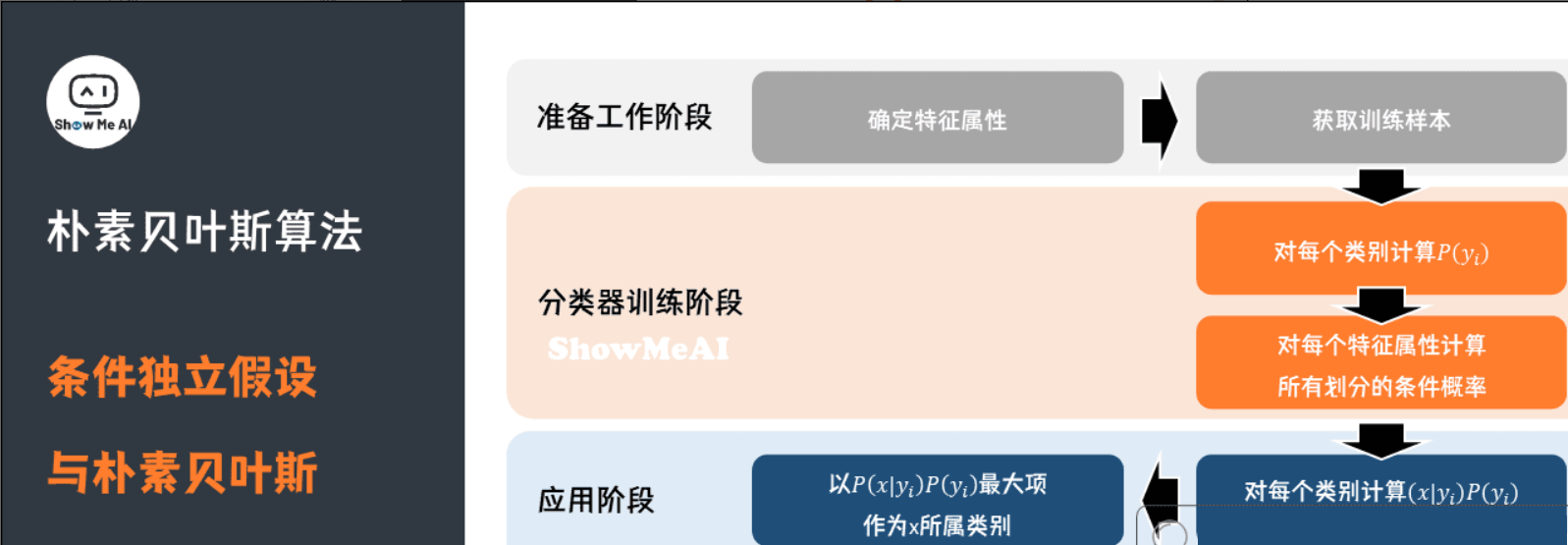
在这里插入图片描述

在这里插入图片描述

总结一下，朴素贝叶斯模型的分类过程如下流程图所示：
在这里插入图片描述

伯努利与多项式朴素贝叶斯
1）多项式vs伯努利朴素贝叶斯

大家在一些资料中，会看到「多项式朴素贝叶斯」和「伯努利朴素贝叶斯」这样的细分名称，我们在这里基于文本分类来给大家解释一下：
在这里插入图片描述

在文本分类的场景下使用朴素贝叶斯，那对应的特征 aj 就是单词，对应的类别标签就是 y ，这里有一个问题：每个单词会出现很多次，我们对于频次有哪些处理方法呢？

如果直接以单词的频次参与统计计算，那就是多项式朴素贝叶斯的形态。
如果以是否出现(0和1)参与统计计算，就是伯努利朴素贝叶斯的形态。

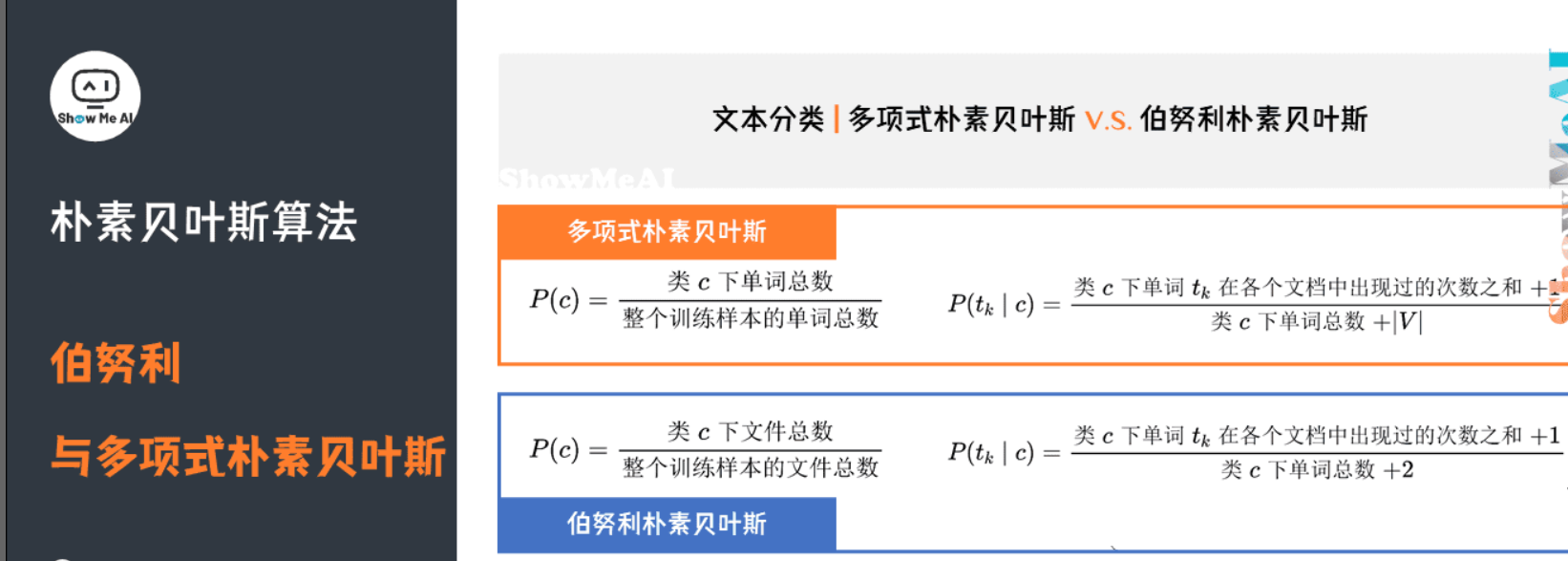
在这里插入图片描述

回到上述例子，如果身高是我们判定人性别（男/女）的特征之一，我们可以假设男性和女性的身高服从正态分布，通过样本计算出身高均值和方差，对应上图中公式就得到正态分布的密度函数。有了密度函数，遇到新的身高值就可以直接代入，算出密度函数的值。
在这里插入图片描述

最烧脑的悖论，意识为什么会影响未来

参考：最烧脑的悖论，意识为什么会影响未来？颠覆你认知的三门问题

今天的内容足以颠覆你对世界的认知。在一道极为简单的数学问题上，98%的人都做了错误的选择。我们先从法外狂徒张三说起，张三落网后，和李四、王麻子关押在同一所天牢。恰逢新皇登基，大赦天下，要对一批死囚犯进行赦免。然而张三、李四、王麻子这三个死囚中，只能释放一个人，另外两个人将被处死。当消息传到天牢的时候，这三个人都喜出望外，因为都有被释放的一线可能。但在欢喜过后，又是无尽的恐怖，他们不知道谁会被释放。法外狂徒张三的大脑在飞速的运转，他便跟看守套近乎，欲获得情报。可是看守根本就不吃这一套，半个字都没说。
在这里插入图片描述

于是他启动逆向思维问看守：现在都知道3个囚犯当中有两个会被处死，只有一个人被释放。李四和王麻子这两个人中必有一人被处死，即便我知道这二人当中，谁会被处死，对我来说也并没有什么好处。那么，你能不能告诉我，谁还会被处死呢？”看守听后觉得很有道理，就告诉他，李四会被处死。得到这个消息后，张三兴奋不已。
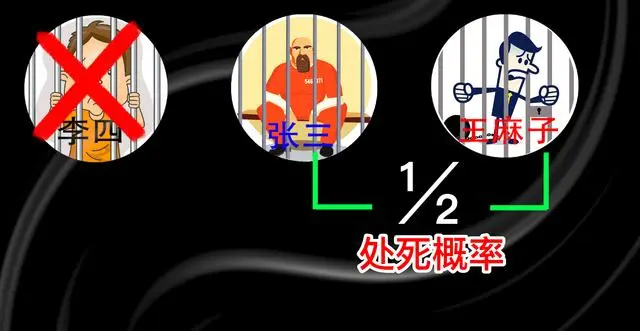
在这里插入图片描述

他认为李四被处死，自己和王麻子被释放的概率就从1/3上升到了1/2。按照张三的逻辑，他被处死的概率同样也会变为1/2。屏幕前的你，是不是和张三算出的概率一样呢？但是你知道吗这个结果是错误的。正确的答案是：李四被处死，张三被释放的概率不变，王麻子被释放的概率将提升至2/3。这是为什么呢？稍后我会专门讲到。现在我们还得从全世界智商最高人说起。
在这里插入图片描述

三门问题-让我们做个交易吧

其实这个问题源自1970年，美国纽约电视台创办的一个电视游戏节目，叫做《让我们做个交易吧》。主持人在台上放置了三扇关闭了的门，其中一扇门的后面藏着一辆跑车，其余两扇门的后面藏的则是更为便宜的东西，比如说其它两扇门的后面藏的是羊。游戏的规则就是让参与者从这三扇关闭的门中做出选择，如果参与者选中了藏有跑车的门，那么他将会获得奖品就是这辆跑车，如果选择的门后面没有跑车而是羊，
则挑战失败，没有任何奖品。对于每一个参与者来说，肯定是想选中藏着跑车的那扇门。
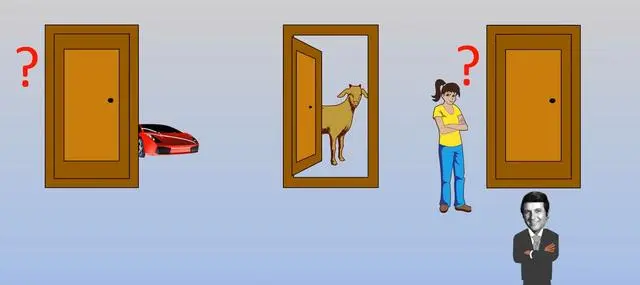
在这里插入图片描述

刚开始的时候，游戏规则还是比较简单的，就是嘉宾随意选一个门，主事人打开。要是抽中跑车，那就赚到了。大家看明白了吗？不论你选择开哪一扇门，中奖的概率都是1/3。几期节目之后，主持人认为这样的规则太过单调，缺乏舞台的活力。于是他在游戏环节中和参与者打心理战，经常突如其来地变换游戏规则，给参赛人和观众都来个猝不及防，既使得观众们困惑不已，又迫使参赛者“脑筋急转弯”。具体操作是这样的，在参与者选定一扇门之后，主持人并不急于的打开参与者选择的那扇门，宣布游戏的结果。而是选择打开另一扇藏着山羊的门。这里需要说明的是，主持人是知道跑车在哪扇门后面的。然后问参与者是否换门。
在这里插入图片描述
比如当一位参与者选中了1号门之后，主持人则打开了2号门，2号门后门则是一只羊。这个时候主持人就会问参与者，你要不要换门？我想大部分人的第一反应，和参与者是一样的，换门和不换门有什么区别吗？一共就只有三扇门，打开了一扇藏着羊的门。剩下的两扇门中，必定有一扇能够中奖，一扇不能。换不换的概率不都是1/2吗？这个时候你会作何选择呢？大部分的观众都支持不换门，参与者也认为换门没有意义，于是就没有换门。结果1号门的后面是一只羊。
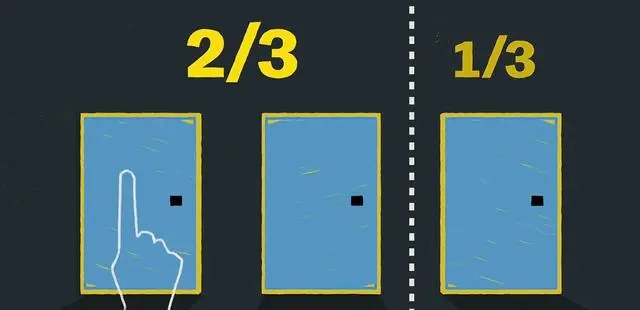
在这里插入图片描述

这个节目非常的火爆，但是参与者却没有严肃的思考过是否应该选择换门这个问题。这个时候有人就想到了智商最高的人玛丽莲·沃斯·莎凡特。并写信问她，你帮忙给推算推算，从科学的角度，到底该不该换门呢？经过一番思索之后，玛丽莲回复的是“应该换门”。玛丽莲认为换门后获胜的概率是不换门的两倍。也就是说换门的取胜概率为2/3，不换门则为1/3。
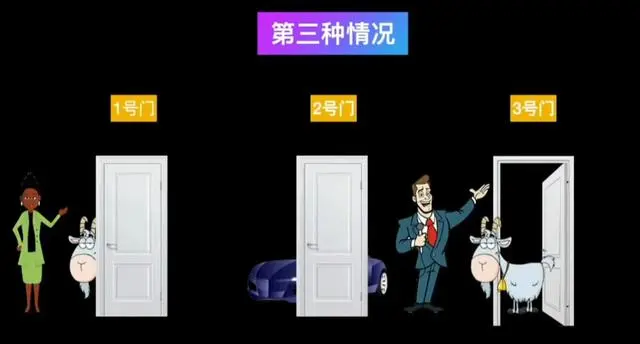
在这里插入图片描述

在玛丽莲收到读者的信后，就根据游戏画了一张图，她认为这个游戏只能出现以下的三种情况。参与者选择了一扇门，主持人打开了藏有羊的门，如果参与者换门出现的第一种情况，参与者选中了有跑车的门，换到了有羊的门；
在这里插入图片描述

第二种嘉宾选择了一扇有羊的门，主持人打开了一扇有羊的门，如果这个时候换门，刚好获得跑车。
在这里插入图片描述

第三种情况和第二种情况差不多，参与者选择了一扇有羊的门，主持人打开了有羊的门，那只要参与者选择换门，就会获得跑车。
在这里插入图片描述

在第二种或第三种的情况里，参与者只要选择换门，就会获胜。所以玛丽莲得出的答案就是，只要参与者选择换门，获胜的概率就会提升到2/3。
在这里插入图片描述

玛丽莲计算的结果，和我们的直觉似乎背道而驰，直觉告诉我们换门与不换门中奖的概率都是1/2，玛丽莲的答案却是2/3。这和前面张三被释放的概率一模一样。

在这里插入图片描述
1978年5月11日，《光明日报》发表本报特约评论员文章《实践是检验真理的唯一标准》，这句话放在任何国家或任何领域，永远都不会过时。网上有一个网名叫做西到咸鱼的计算机大神，他认为检验玛丽莲计算的结果是否正确的唯一办法，就是通过计算机对游戏进行反复的演算。于是他单独编写了一套程序，取名为《三门问题的验证》。
在这里插入图片描述

他用这个程序进行了10万次的推演，不换门赢得跑车的次数是33115次，换门后赢得跑车的次数为66885次。根据西到咸鱼实验的数据来看，换门后获奖的概率和玛丽莲计算出的概率很相似，提升到2/3。看来玛丽莲没有算错。

在这里插入图片描述

将3个门记为1,2,3号，假设参赛者先选择的是1号门。

假设主持人开启了2号门，这个事件记为D。那么参赛者坚持选择或是改变选择而赢得汽车的概率又是多少？
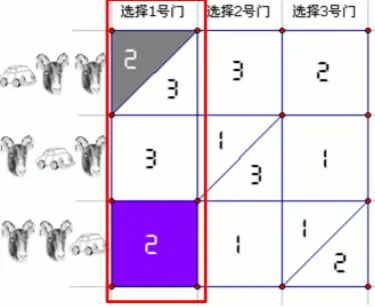
在这里插入图片描述
从图中的第一列看出，当参赛者选择了1号门， 2号门被打开的概率P(D)=1.5/3；汽车在1号门并且主持人打开了2号门的概率P(AD)=0.5/3 。
坚持选择：P(A|D)=P(AD)/P(D)=1/3
改变选择：P(CD)=1/3 P(C|D)=P(CD)/P(D)=2/3