287.给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
示例 1：
输入：nums = [1,3,4,2,2]
输出：2
示例 2：
输入：nums = [3,1,3,4,2]
输出：3
示例 3 :
输入：nums = [3,3,3,3,3]
输出：3
提示：
1 <= n <= 10^5
nums.length == n + 1
1 <= nums[i] <= n
nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次
进阶：
如何证明 nums 中至少存在一个重复的数字?
你可以设计一个线性级时间复杂度 O(n) 的解决方案吗？

• 为了只使用 O(1) 的额外空间，我们借用原数组的空间做标记，找到结果后复原数组。具体思路如下：由于数组中的数都小于数组长度 n+1，所以每个 nums[i] 都能对应一个数组下标，比如 nums[0]=3，我们令其指向数组下标为 3 的地方，将 nums[3] 标记为负数，这就表示数组中存在一个数为 3，若所有数不重复，那么最后每个 nums[i] 都会指向对应的位置且位置不重复；而如果存在重复的数就会有：要标记时被标记数已为负数

•   public int findDuplicate(int[] nums) {
        int res = nums[0];
        for(int n:nums){
        	// 因为这个位置上的数可能被标记为负数，所以取绝对值
            int a = Math.abs(n);
            // 将对应位置上的数标记为负数
            if(nums[a]>0)nums[a]=-nums[a];
            // 否则说明已经标记过了，此时 a 为结果
            else res = a;
        }
        // 复原
        for(int i=0;i<nums.length;i++){
            nums[i]=Math.abs(nums[i]);
        }
        return res;
    }
  

• 他人题解：把数组看做环形链表，上面说了每个 nums[i] 都能对应一个数组下标，那么就把 nums[i] 看做下一个节点的下标，我们把数组下标与值一一对应，可以得到类似链表的结构，例如[1,3,4,2,2]我们可以得到：

• 0 -> 1
  1 -> 3
  2 -> 4
  3 -> 2
  4 -> 2

• 我们从下标 0 开始，根据 nums[0] 得到一个值 n，然后从这个值继续，以他为下标，可以得到 nums[n]，他就是新的 n，然后继续得到 nums[n]…
• 也就是说上面例子可以看做 0->1->3->2->4->2->4->2->…，其中的 2->4 为一个循环，可以看做如下链表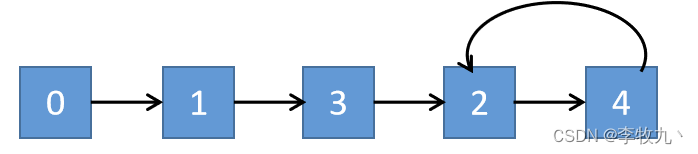
• 由于有重复的数，所以一定会产生多对一的映射，并且因为 nums[i] 的范围为 [1,n]，而数组长度为 n+1，所以不可能导致链表中断，一定会得到环。
• 举个不符合规则的测试用例 [1,3,2,4]，会得到链表 0->1->3->4->null，这里就是没有 nums[4] 所以链表中断了，但是实际上 nums[i] 的范围被限制为 [1,3]，所以不会出现这个例子的情况
• 那么最后本题中找到重复的数就被我们转化为了找到环的入口，因为只有重复的数才能满足环的起点和终点一样的特点
• 接下来分析怎么得到环的入口，使用快慢指针，首先当两个点相遇时，能相遇的原因就是快指针进行了无用功，比如跑了一个环的长度回到了原地，所以被慢指针追上了，设环长度为 m，慢指针走了 x 步，那么快指针和它相遇肯定是走了 x+ym 步（y=1,2,3…，表示比慢指针多跑了 y 圈环的长度）。那么两点第一次相遇时，慢指针步数为 x，快指针步数为 x+m，这个 x 是多少步？因为快指针的速度是慢指针的两倍，所以快指针步数 x+m 等于慢指针步数 x 的两倍 => x+m=x+x => x=m，也就是说快慢指针第一次相遇时慢指针走了 m 步，设相遇点离环起点 n 步，环起点离原点就有 m-n 步，同时，从相遇点继续走到环起点也需要 m-n 步，那么此时就让慢指针回到原点，快指针开始一步一步走，最后经过 m-n 步，两个指针就同时到达了环起点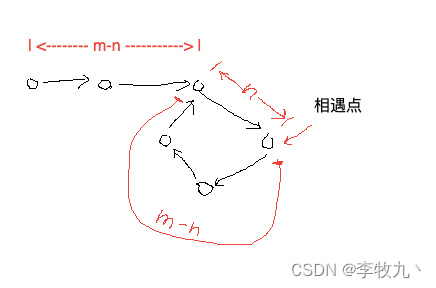
• 如上图的例子，两点会在环的长度也就是第四个点处第一次相遇，此时快指针再走三步到环起点，慢指针也是走三步到环起点

•   public int findDuplicate(int[] nums) {
        int slow = 0,fast = 0;
        // 初始走一下，不然直接相等了
        slow = nums[slow];
        fast = nums[nums[fast]];
        // 第一次相遇时停止
        while(slow != fast){
            slow = nums[slow];
            fast = nums[nums[fast]];
        }
        // slow 回原点
        slow = 0;
        // 共同走 m-n 步在环起点相遇
        while(slow != fast){
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }