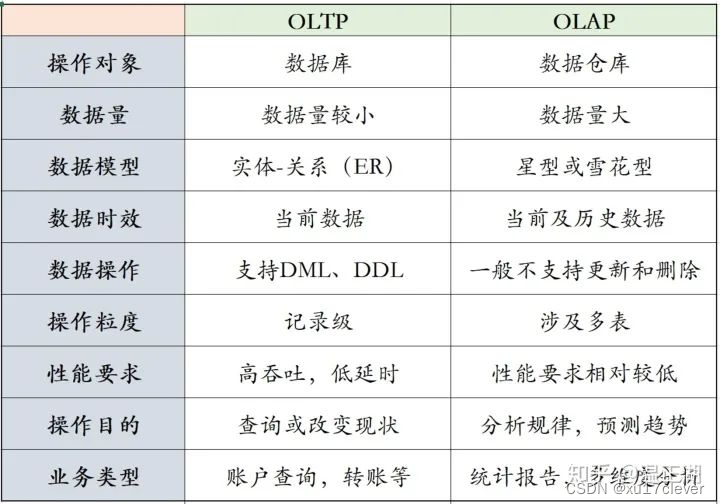
总结
(PS:这次竞赛的奖励对我诱惑力感觉没多大,因为高级背包不久前才收到一个,邹老师的两本签名书也早就拿到了,程序员杂志、帆布包也都有了,扑克牌都拿了几副了,所以还是换点其他的书比较好,拿那么多的背包也用不上)。建议后面奖励如果拿重了可以换其他的,多来点深度学习之类的书籍就好了。
这次的题目难度偏低,只有T2可能数据有点问题,开始提交一个代码通过了部分用例,检查下发现有bug,修改后用例通过率变成0了,到最后没时间了只好用最开始的代码提交了。提交后发现大家都还没得分,就挺诧异的,看来还是得看运气。
题目列表
1.合并序列
题目描述
有N个单词和字符串T,按字典序输出以字符串T为前缀的所有单词。
输入描述:
输入文件第一行包含一个正整数N;
接下来N行,每行一个单词,长度不超过100;
最后一行包含字符串T。
所有字符均为小写字母。
输出描述:
按字典序升序输出答案。
输入样例:
6
na
no
ki
ki
ka
ku
k
输出样例:
ka
ki
ki
ku
分析
求前缀第一反应是trie树,当然本题只需要读入后使用string的sunstr方法直接判断前缀是否相等即可,将前缀等于T的单词存入vector中,排下序就可以输出了。主要本题的输入可能有重复的字符串,因此不能使用set存储。
代码
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
int n;
vector<string> str;
string x, T;
cin>>n;
for (int i = 0; i < n; i++) {
cin>>x;
str.push_back(x);
}
cin>>T;
int len = T.size();
vector<string> res;
for (auto t : str) {
if (t.substr(0, len) == T) res.push_back(t);
}
sort(res.begin(), res.end());
for (auto t : res) cout<<t<<endl;
return 0;
}
2.千问万问
题目描述
给定大小为n的整数序列A.
现在会有q次询问,询问子区间的不同整数的数量。
输入描述:
第一行输入整数n,q.(1<=n,q<=1000)
第二行输入n个整数.(1<=a<=100000)
以下q行每行两个整数l,r。(1<=l,r<=100000)
输出描述:
输出区间内的整数数量。
输入样例:
10 3
1 2 3 4 5 6 7 8 9 10
1 1
1 2
1 3
输出样例:
1
2
3
分析
本题数据范围给定不大,完全可以使用hash存储10w以内每个数出现的次数,然后再使用一个前缀和数组来维护hash数组的前缀和,就可以在O(1)的时间内求出区间内的整数数量了,这样以来总的计算次数也是 O ( 1 0 5 ) O(10^5) O(105)的。
再来说下题目的bug,题目描述里说要统计不同整数的数量,而输出描述里则是说统计区间内整数的数量,这两个语义是不一致的。至于题目输入模板的bug,一开始我就删掉了模板自己写了,倒是没有注意到。这里我按照统计整数的数量去写,不管整数是否重复,可以通过三成的用例,当然我记得竞赛题目的输入范围不是从1开始的,而是从0开始的,所以下面的代码没有统计0是有问题的,但是奇怪的是如果我统计上0,用例通过率就变成0了,大概是标杆程序对区间的处理存在问题,所以存在bug的代码误打误撞的过了几个用例。
代码
#include <iostream>
#include <string>
#include <sstream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int N = 100005;
int a[N], s[N];
int main() {
int n, m, x;
cin>>n>>m;
memset(a, 0, sizeof a);
memset(s, 0, sizeof s);
for (int i = 0; i < n; i++) {
cin>>x;
a[x]++;
}
for (int i = 1; i <= N - 1; i++) s[i] = s[i - 1] + a[i];
while(m--) {
int l, r;
cin>>l>>r;
cout<<s[r] - s[l-1]<<endl;
}
return 0;
}
3.连续子数组的最大和
题目描述
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和 。(测试用例仅做参考,我们会根据代码质量进行评分)
输入描述:
第一行输入整数数组的大小n。(1<=n<=1000)
第二行给出n个整数a。(-1e5<=a<=1e5)
输出描述:
输出答案。
输入样例:
9
-2 1 -3 4 -1 2 1 -5 4
输出样例:
6
分析
很有纪念意义的一题,经典的DP题目。第一次遇见是在17年912的考卷上,那时候DP都还没有学习。
维护一个变量存储和,当和不小于0时,就加上当前的数,否则和就等于当前的数,取遍历过程中和的最大值即可。
代码
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 100005;
int a[N];
int main() {
int n;
cin>>n;
for(int i = 0; i < n; i++) cin>>a[i];
int res = a[0];
int cnt = 0;
for (int i = 0 ; i < n; i++) {
if (cnt >= 0) cnt += a[i];
else cnt = a[i];
res = max(res, cnt);
}
cout<<res<<endl;
return 0;
}
4.降水量
题目描述
给定n个柱面的高度,表示降雨某地n块区域的海拔高度。
计算降雨之后该地最大储水面积。如果低于地平线,也就是小于0,则一定积水
输入描述:
第一行输入整数n.(1<=n<=10000)
第二行输入n个高度整数h。(-10000<=h<=10000)
输出描述:
输出答案。
输入样例:
12
0 1 0 2 1 0 1 3 2 1 2 1
输出样例:
6
分析
本题属于接雨水的变形,与接雨水问题不同的是,柱面的高度可能小于0,小于0的一定储水。
首先,考虑下什么情况下一定会储水,只要柱子左边和右边都存在比它高的柱子,就一定会储水,n个柱子的两边可以认为有两个高度为0的柱子哨兵,这样一来,高度小于0柱子的积水也会被统计上。
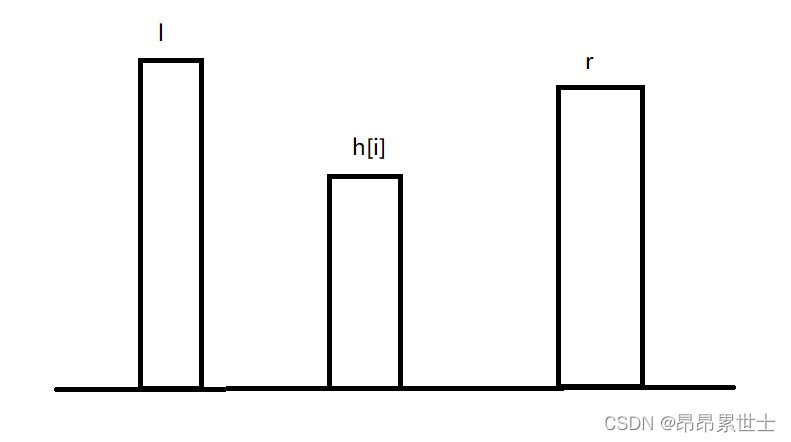
如图所示,第 i i i柱子上的积水高度等于 m i n ( l , r ) − h [ i ] min(l,r)-h[i] min(l,r)−h[i],其中 l l l表示 i i i左边柱子的最大高度, r r r表示 i i i右边柱子的最大高度,只要 h [ i ] h[i] h[i]比左右两边最高的柱子高度都小,就可以积水了。因此,比较简单的一种做法就是统计下自左向右和自右向左的柱子最大高度,然后遍历一下求出每根柱子的积水之和即可。
代码
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 10005;
int h[N], l[N], r[N];
int main() {
int n;
cin>>n;
for (int i = 1; i <= n; i++) cin>>h[i];
int t = 0;
for (int i = 1; i <= n; i++) {
l[i] = t;
t = max(t, h[i]);
}
t = 0;
for (int i = n; i >= 1; i--) {
r[i] = t;
t = max(t, h[i]);
}
int res = 0;
for (int i = 1; i <= n; i++) {
t = min(l[i], r[i]);
if (h[i] < t) res += t - h[i];
}
cout<<res<<endl;
return 0;
}