目录

💥1 概述

📚2 运行结果

🎉3 参考文献

👨‍💻4 Matlab代码

---

💥1 概述

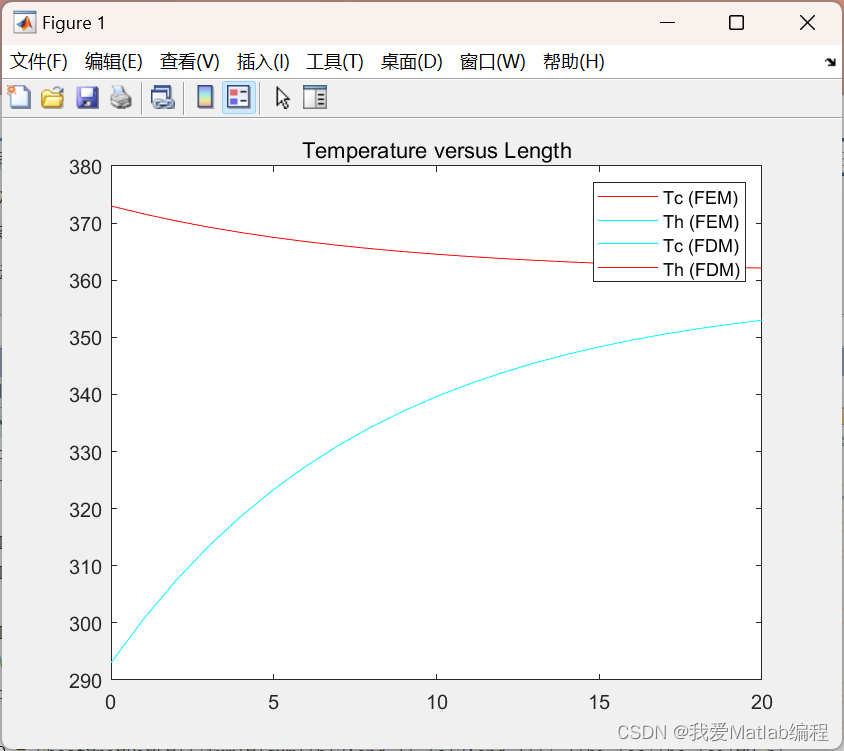
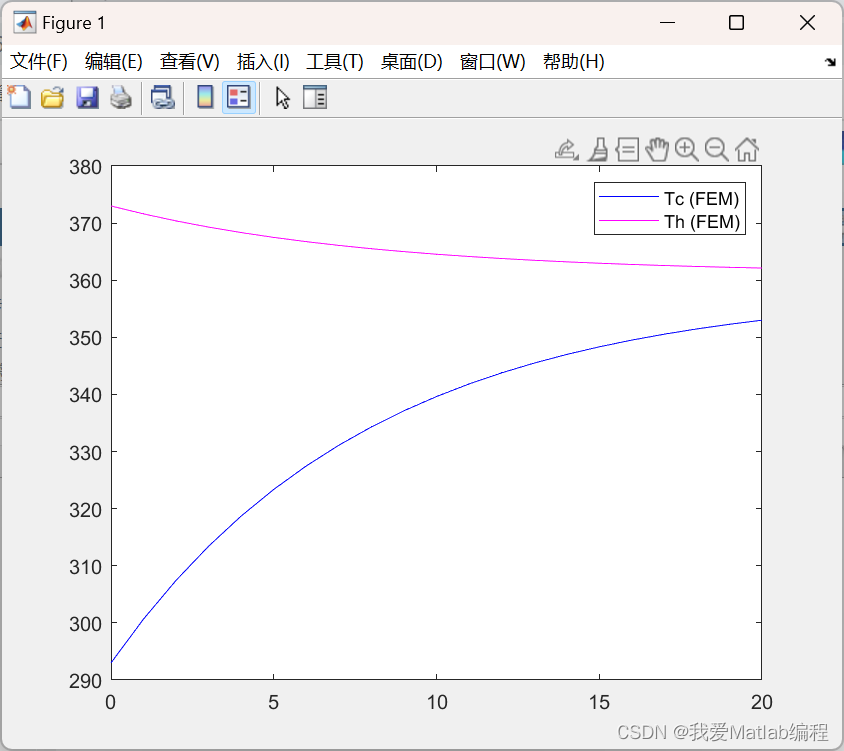
1. 首先试图对热交换器的设置进行建模，并获得该过程的控制方程。
2. 使用相应的控制方程并设置边界条件并获得适当的边界值问题。
3. 执行案例研究并将设置建模为上述 BVP。
4. 使用有限元法或有限差分法，找出未知温度分布并求解未知。
5. 找出与问题相关的其他物理量。

📚2 运行结果

 

 

🎉3 参考文献

[1]王子介,G.KRAUSS,张丛智.热交换器的微元模拟法及求解[J].制冷学报,2000(01):33-39.

👨‍💻4 Matlab代码

主函数部分代码：

rhoc = 1060; %kg/m3
rhoh = 1000; %kg/m3

Cpc = 805; %J /Kg-K
Cph = 4187;%J /Kg-K

kc = 0.38;  %W/m-K
kh = 0.6408;%W/m-K

vc = 1; % m/s
vh = 2; % m/s

D0 = 0.01;
Di = 0.008;
Dhyd = D0 - Di;

Vdotc = pi*(Di^2)*0.25*vc;
Vdoth =  pi*(D0^2 - Di^2)*0.25*vh;

hc = 4.36*kc/Di;
hh = 4.36*kh/Dhyd;

Uheat = 1/((1/hc)+(1/hh));

mc = rhoc*Vdotc*Cpc; %W/K
mh = rhoh*Vdoth*Cph; %W/K

eta = 1 + (mc/mh);
Uc = Uheat*pi*Di*eta; %W/m-K

M = mc;
U = Uc;
L = 20;
Num = 20;
l = L/Num ;
Tci = 293;
Tco = 353;

Thi = 373;

mt0 = mc*Tci + mh*Thi;

a = (M/(l^2)) + (U/(2*l));
b = (M/(l^2)) - (U/(2*l));
c = 2*M/(l^2) ;
T = zeros(Num+1,1);
T(1,1) = Tci;
T(end,1) = Tco;
T(2:end-1,1) = 0.5*(Tci + Tco);
N = 500 % Number of Iterations
for i = 1 : N
    for j = 2:(Num)
        T(j,1) = (a/c)*T(j+1,1) + (b/c)*T(j-1,1);
    end
    
end