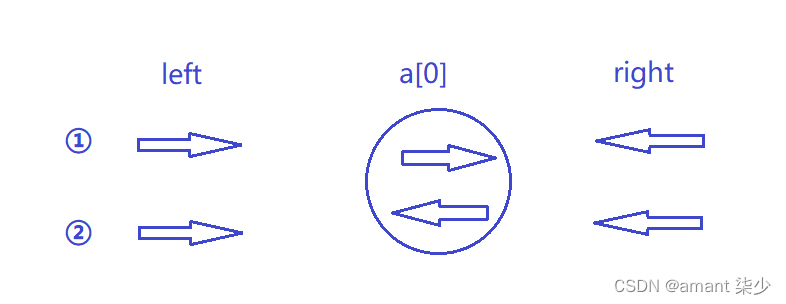
二叉树的遍历
遍历二叉树, 是指按一定的规则和顺序访问二叉树的所有结点, 使每一个结点都被访问一次, 而且只被访问一次.
由于二叉树是非线性结构, 因此, 二叉树的遍历实质上是将二叉树的各个结点排列成一个线性序列.
DFS: 前序, 中序及后序.
BFS: 是指沿着二叉树的宽度优先遍历二叉树的结点, 即从上到下从左到右逐层遍历二叉树的结点.
前序遍历
访问根结点(N), 前序遍历左子树(L), 前序遍历右子树®, 也即NLR.
也可以是NRL, 因为这两种遍历方法都是先访问根结点, 所以没有区别, 掌握其中一种, 另一种也随之掌握.
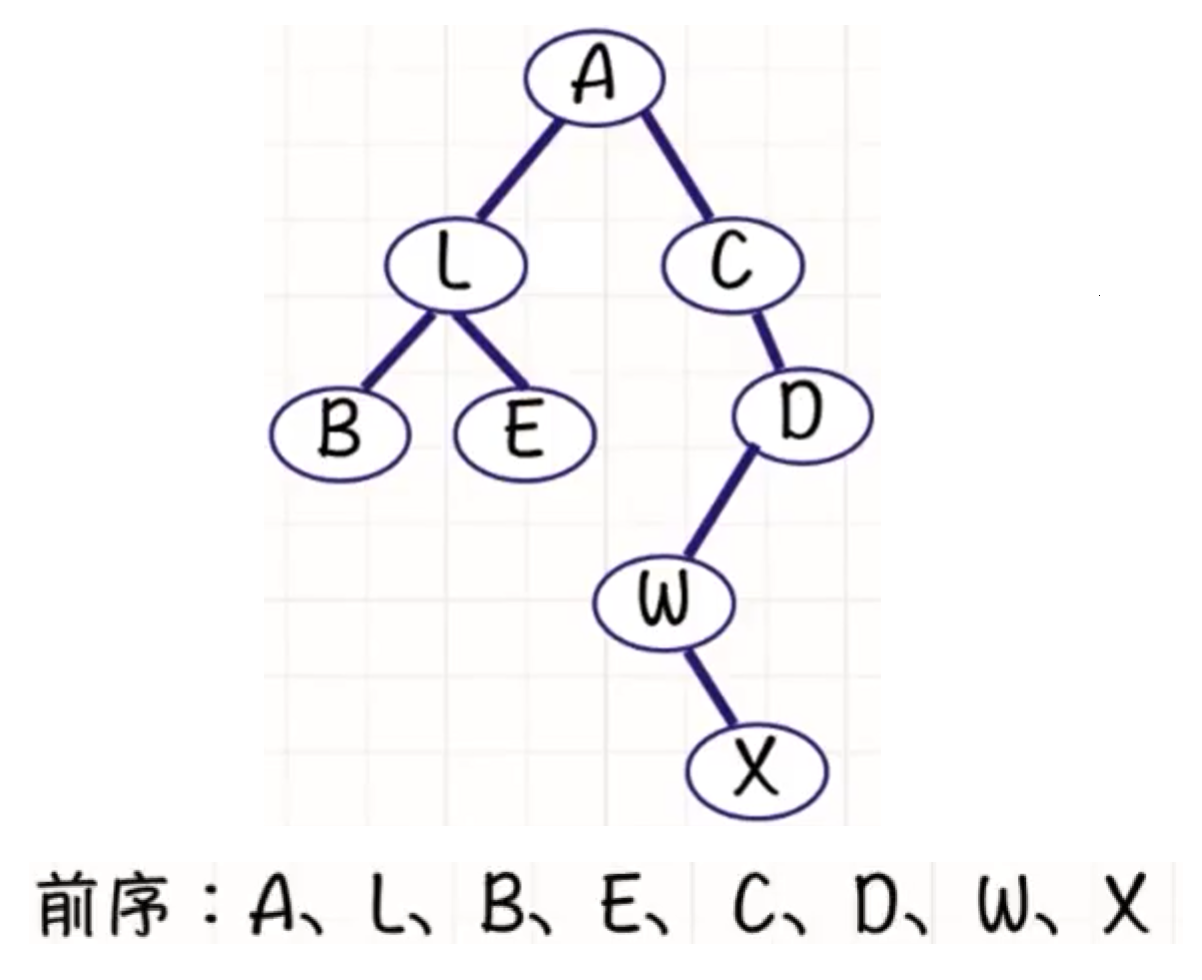
给你二叉树的根节点
root,返回它节点值的 前序 遍历。
非递归思路: 二叉树的前序遍历
- 对于给定根结点root, 依次从根结点root向左路结点遍历, 直到curr为空并在遍历途中访问对应结点的val, 然后将结点依次入栈.
- 当curr为空时, pop栈顶结点, 将栈顶结点的右子树根结点赋值给curr, 并继续转换成从根向左路遍历.
// 二叉树的前序非递归遍历
vector<int> preorderTraversal(TreeNode* root)
{
stack<TreeNode*> st;
vector<int> v;
TreeNode* curr=root;
while(curr!=nullptr||!st.empty())
{
while(curr!=nullptr)
{
v.push_back(curr->val);
st.push(curr);
curr=curr->left;
}
TreeNode* top=st.top();
st.pop();
curr=top->right;
/*
// 当curr为空时,遍历左路结点的右子树
if(curr==nullptr)
{
TreeNode* top=st.top();
st.pop();
curr=top->right;
}
else // 当curr不为空时,遍历左路结点
{
v.push_back(curr->val);
st.push(curr);
curr=curr->left;
}
*/
}
return v;
}
中序遍历
中序遍历左子树, 访问根结点, 中序遍历右子树, 也即LNR.
或者RNL.
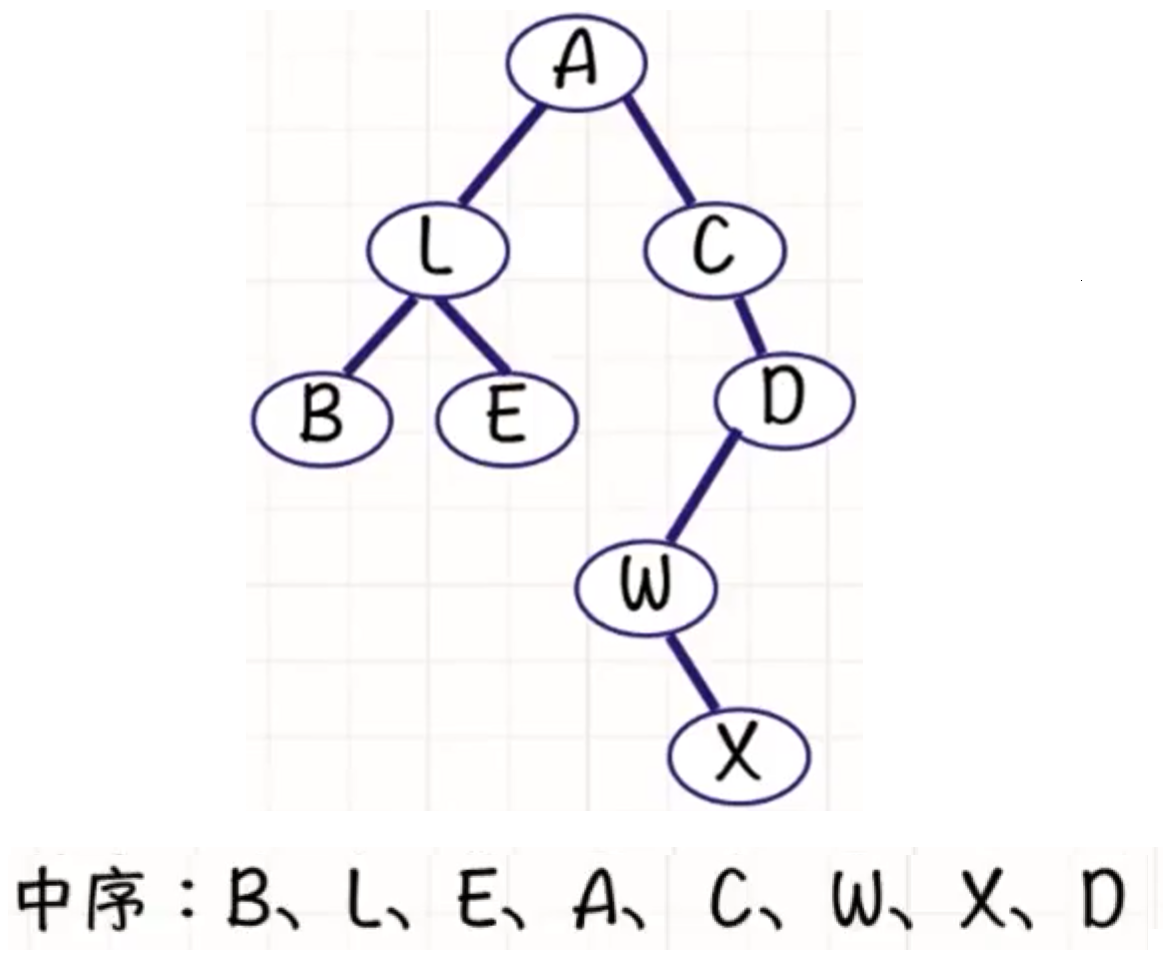
给定一个二叉树的根节点
root,返回 它的 中序 遍历 。
非递归思路: 二叉树的中序遍历
- 中序非递归与前序非递归思路相似, 只是访问结点的val时机不同.
- 对于给定根结点root, 依次从根结点root向左路结点遍历, 直到curr为空并在遍历途中将结点依次入栈.
- 当curr为空时, pop栈顶结点, 先访问栈顶结点的val, 再将栈顶结点的右子树根结点赋值给curr, 并继续转换成从根向左路遍历.
vector<int> inorderTraversal(TreeNode* root)
{
std::vector<int> v;
std::stack<TreeNode*> st;
TreeNode* curr=root;
// 思路与前序遍历相似
while(curr!=nullptr || !st.empty())
{
while(curr!=nullptr)
{
st.push(curr);
curr=curr->left;
}
TreeNode* top=st.top();
st.pop();
// 只是访问TreeNode的val时机不同
v.push_back(top->val);
curr=top->right;
}
return v;
// vector<int> v;
// stack<TreeNode*> st;
// TreeNode* curr=root;
// while(curr!=nullptr || !st.empty())
// {
// if(curr!=nullptr)
// {
// st.push(curr);
// curr=curr->left;
// }
// else
// {
// TreeNode* top=st.top();
// st.pop();
// v.push_back(top->val);
// curr=top->right;
// }
// }
// return v;
}
后序遍历
**后序遍历左子树, 后序遍历右子树, 访问根结点, 也即LRN. **
或者RLN.
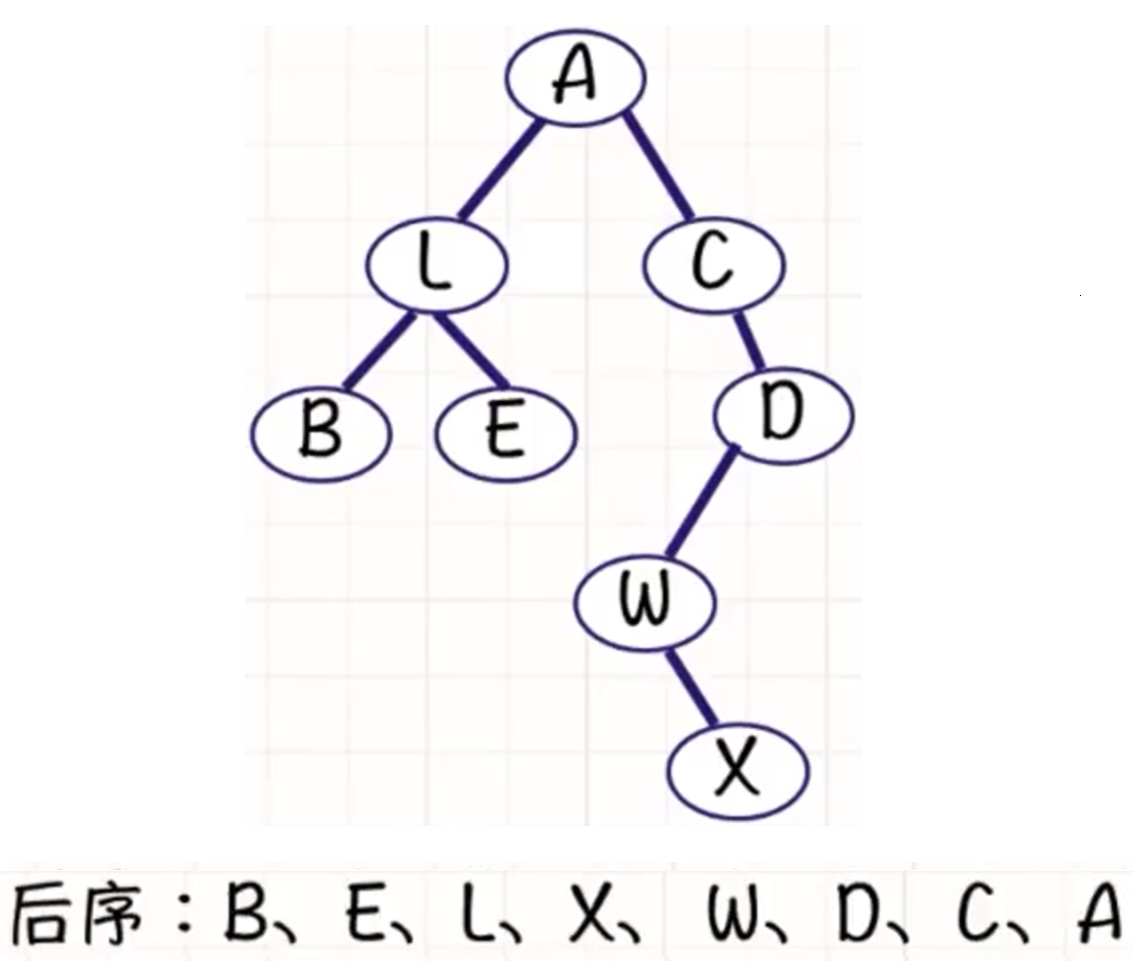
给你一棵二叉树的根节点
root,返回其节点值的 后序遍历 。
非递归思路: 二叉树的后序遍历
- 后序遍历与前中序遍历有一定差异, 在后序遍历过程中, 需要prev来记录访问结点的前一个, 用来判定该不该访问根结点.
- 对于给定根结点root, 依次从根结点root向左路结点遍历, 直到curr为空并在遍历途中将结点依次入栈.
- 当curr为空时, 根据栈顶结点的右孩子right, 来判断是否pop. 如果right为空或者right为prev说明右子树为空或者右子树访问完, 所以可以pop,并访问该栈顶结点的val, 最后更新prev.
- 如果以上两点不满足, 则说明右子树还未访问, 栈顶元素还不能pop, 需要更新curr为栈顶结点的右孩子继续访问.
vector<int> postorderTraversal(TreeNode* root)
{
TreeNode* curr=root;
TreeNode* prev=nullptr; // 记录遍历结点的前一个
vector<int> v;
stack<TreeNode*> st;
while(curr!=nullptr || !st.empty())
{
while(curr!=nullptr)
{
st.push(curr); // 将结点入栈
curr=curr->left;
}
TreeNode* top=st.top();
// 当右子树为空或者右子树被访问过,才pop
if(top->right==nullptr || top->right==prev)
{
prev=top;
v.push_back(top->val);
st.pop();
}
else // 否则先访问右子树,等右子树访问完成,才反过来访问根,不能pop
{
curr=top->right;
}
}
/*while(curr!=nullptr|| !st.empty())
{
if(curr!=nullptr)
{
st.push(curr);
curr=curr->left;
}
else
{
TreeNode* top=st.top();
// 当右子树为空或者右子树被访问过,才pop
if(top->right==nullptr || top->right==prev)
{
v.push_back(top->val);
st.pop();
prev=top;
}
else
{
curr=top->right;
}
}
}*/
return v;
}
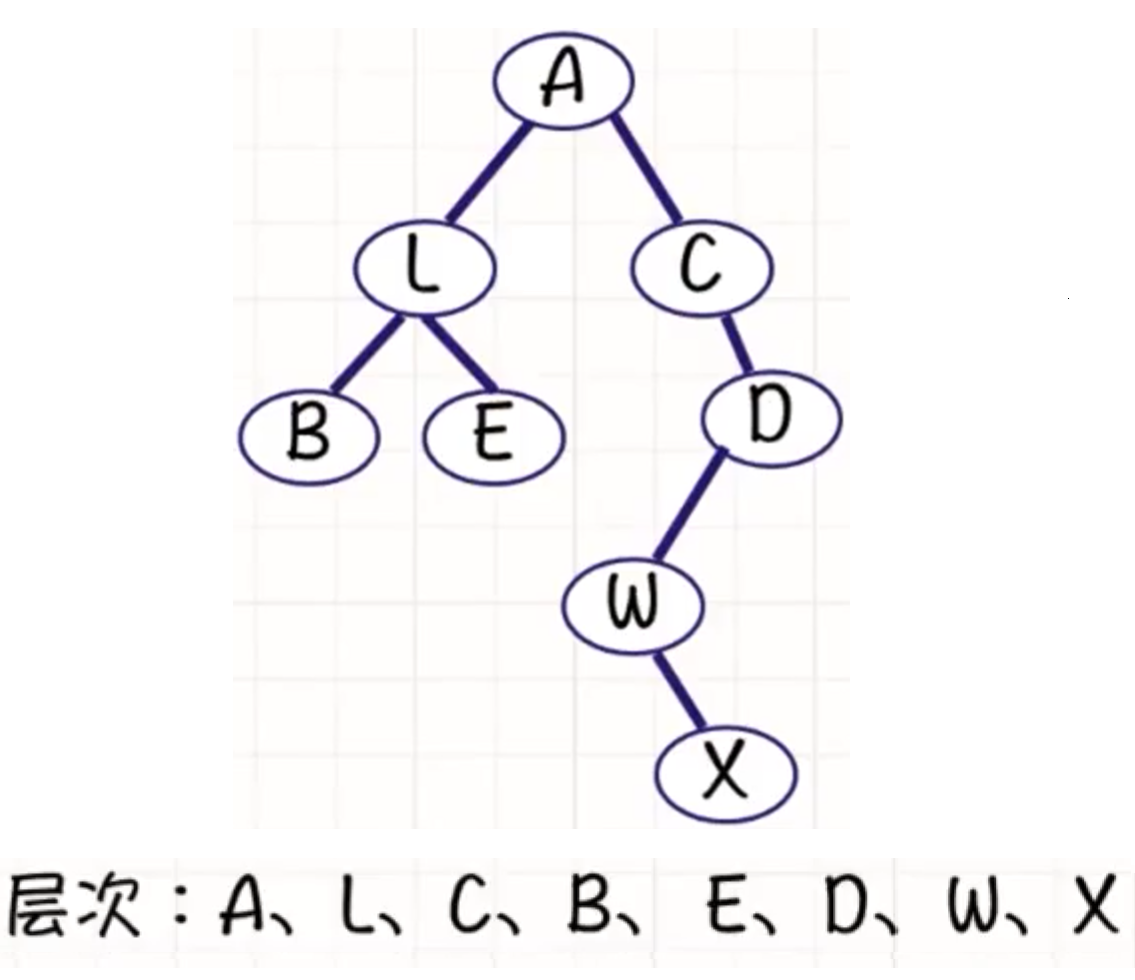
层序遍历
层序遍历就是根据二叉树的结构从上到下从左到右逐层遍历二叉树的结点.
给你二叉树的根节点
root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
基本思路: 二叉树的层序遍历
- 初始化一个队列, 并把根结点入队.
- 当队列非空时, 循环执行步骤3到步骤5, 否则遍历结束.
- 出队一个结点, 并访问该结点.
- 若该结点的左子树非空, 则将其左子树入队.
- 若该结点的右子树非空, 则将其右子树入队.
需要注意: 当某一层走完时, 该层的下一层也随之全部进入队列中.
vector<vector<int>> levelOrder(TreeNode* root)
{
queue<TreeNode*> q;
vector<vector<int>> vv;
int levelSize=0; // 记录某一层有多少个结点
if(root!=nullptr)
{
q.push(root);
++levelSize; // 刚开始根结点这一层就一个结点
}
while(!q.empty())
{
vector<int> v;
// 将该层的结点都遍历完
for(size_t i=0;i<levelSize;i++)
{
TreeNode* front=q.front();
q.pop();
v.push_back(front->val);
if(front->left!=nullptr)
{
q.push(front->left);
}
if(front->right!=nullptr)
{
q.push(front->right);
}
}
// 遍历完成,队列中的个数就是下一层结点的个数
levelSize=q.size();
vv.push_back(v);
}
return vv;
}
if(front->right!=nullptr)
{
q.push(front->right);
}
}
// 遍历完成,队列中的个数就是下一层结点的个数
levelSize=q.size();
vv.push_back(v);
}
return vv;
}