leetcode 209. 长度最小的子数组 | 中等难度

1. 题目详情

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组[numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

进阶：
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

1. 原题链接

leetcode 209. 长度最小的子数组

2. 基础框架

● Cpp代码框架

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {

    }
};

2. 解题思路

1. 题目分析

$(1)$ 本题数组nums都是正整数，target也是正整数。要求找出其中大于等于target的最短连续子数组（序列）。

$(2)$ 暴力遍历算法是我们首先想到的方法，枚举出所有的可能情况，找出符合题目的结果。时间复杂度$O(n^2)$。

$3）$ 在暴力遍历时先定位一个位置left，从这个位置left开始，向右依次遍历所有元素。
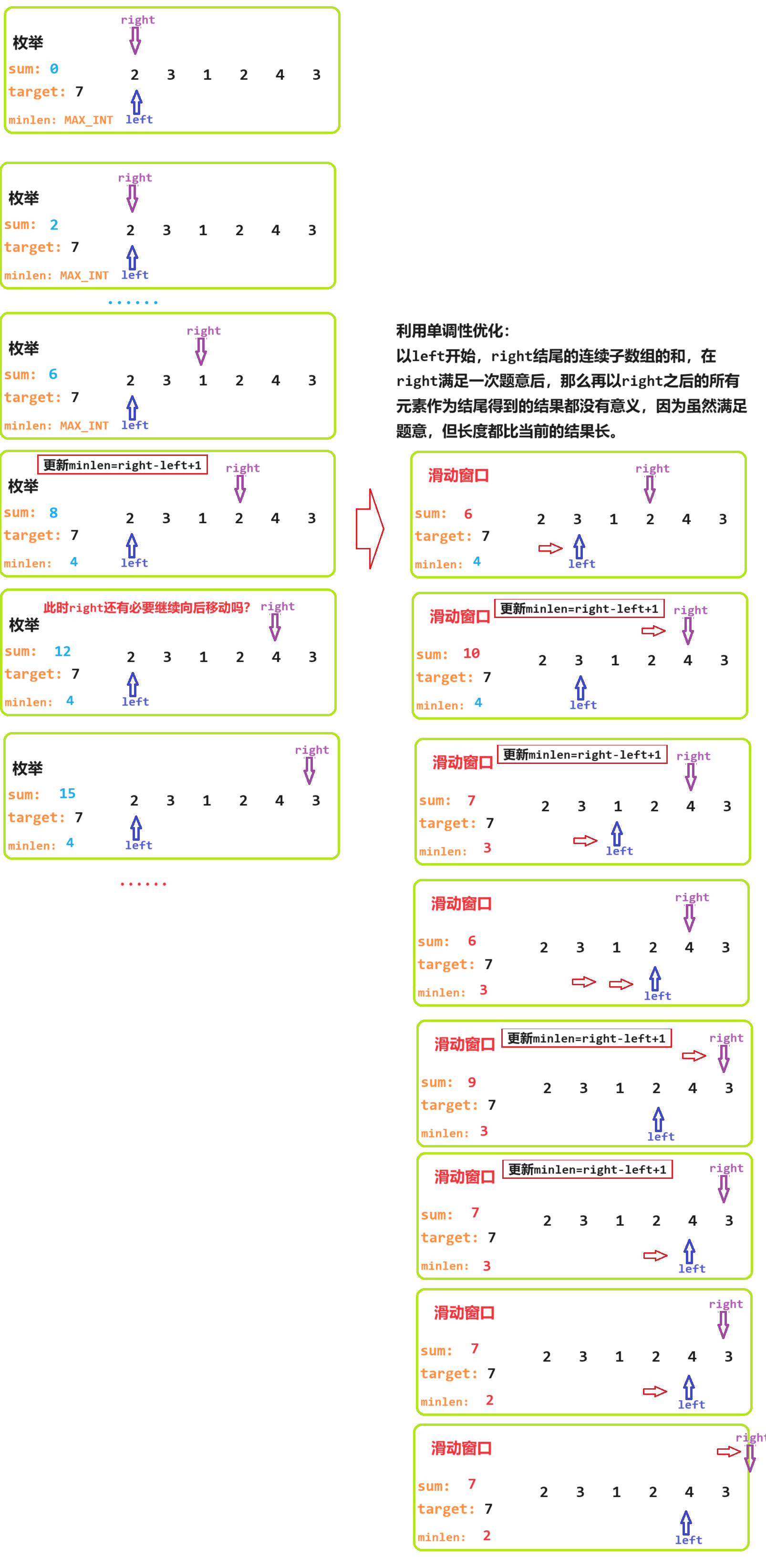
假设在某个位置j满足了连续子数组大于等于target的条件，那么right之后的所有位置都没有必要再遍历了，因为数组的元素全是正整数，连续子数组的和sum一定是增大的，但是连续子数组的长度len也增大了，而题目中是要找最短的。所以i位置相当于已经判断完毕，可以直接判断以left+1位置为起始的连续子数组的是否满足题意了。

$4）$ 优化之法就在隐藏在暴力解法之内：无需重新从left+1位置开始遍历，直至right计算连续子数组的和，而是sum减去left位置的元素就得到了从left+1到right的连续子数组的和。
这里面隐藏的规律是：

1. 单调性：从left开始的连续子数组的和sum一定是增大的，长度len一定是增大的；
2. left和right指针（或者说是下标）移动的方向是同向的，且不会回退到已经移动的位置。
   而上述所说的优化，即同向双指针，又形象的称为滑动窗口。指针left和right分别相当于滑动窗口的左边界和右边界，滑动窗口内的所有元素的特点就是连续且长度最短且之和sum大于target。
   

2. 算法原理

$(1)$ 初始化
左右边界left=0,right=0。
$(2)$ 进窗口
每次进入循环，都让sum+=nums[right]，即让新元素进入窗口。

$(3)$ 判断条件
如果sum < target，即left和right范围内所有元素的和小于目标值，此时需要继续让新元素进窗口，即right++。
如果sum >= target，即窗口内所有元素的和大于等于目标值；

$(4)$ 更新结果
在sum >= target时，连续子数组的和满足了条件，即得到了一个结果长度curlen = right - left + 1，需要把得到的结果长度curlen与当前的最短长度minlen取得最短的更新minlen的值。

$(5)$ 出窗口
在sum >= target时，以left为起点的连续子数组的和到right位置就已经满足题意了，right后的所有元素没有必要判断了，故让当前left位置元素出窗口，即sum-=[left]且left右移left++；之后返回第三步的判断条件处，继续判断sum与target的关系，直到满足sum<target时结束判断，然后进入下一次循环。

$(6)$ 滑动窗口有着基本的解题思路，上述的第四步更新结果不一定是在判断条件满足之后才更新的（本题是这样），这与具体的题目要求相关。也可能是在进入循环且判断条件之前就可以更新结果，也可能是在结束整个循环后才更新结果（全部结束时）。

3. 时间复杂度

$O(n)$

只看代码来说，也许你会认为时间复杂度是$O(n^2)$，其实这并不正确。在我们对滑动窗口进行分析时，left和right同向移动且不回退，最差的情况是left走到n，right走到n，二者是相加的关系，即时间复杂度是O(n)。

3. 代码实现

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int minlen = INT_MAX;
        int l =0, r = 0;
        int sum = 0;
        while(r < nums.size()){
            sum += nums[r];// 1.进窗口
            while(sum >= target){// 2.判断
                minlen = min(minlen, r - l + 1);// 4.更新结果
                sum -= nums[l];// 3.出窗口
                l++;
            }
            r++;
        }
        return minlen == INT_MAX ? 0 : minlen;
    }
};

4. 知识与收获

$(1)$ 滑动窗口（同向双指针）本质就是基于求解过程中隐藏的单调性特点，帮助我们省去了众多无效的判断。
$(2)$ 每一次循环都会让新元素进入窗口，窗口内元素的和也增加；
$(3)$ 在旧元素从左侧出窗口时是循环出去的方式，因为一次只会出一个元素，而出元素之后的和可能还是大于等于目标值；

---

$The$ $End$