循环神经网络 - 参数学习之随时间反向传播算法

本文中，我们以同步的序列到序列模式为例来介绍循环神经网络的参数学习。

循环神经网络中存在一个递归调用的函数 𝑓(⋅)，因此其计算参数梯度的方式和前馈神经网络不太相同。在循环神经网络中主要有两种计算梯度的方式：随时间反向传播(BPTT)算法和实时循环学习(RTRL)算法。

本文我们来学习随时间反向传播算法。

BPTT 算法将循环神经网络看作一个展开的多层前馈网络，其中“每一层”对应循环网络中的“每个时刻”。这样，循环神经网络就可以按照前馈网络中的反向传播算法计算参数梯度。在“展开”的前馈网络中，所有层的参数是共享的，因此参数的真实梯度是所有“展开层”的参数梯度之和。

一、数学推导：

以随机梯度下降为例，给定一个训练样本 (𝒙, 𝒚)，其中 𝒙1∶𝑇 = (𝒙1, ⋯ , 𝒙𝑇 )为长度是𝑇的输入序列，𝑦1∶𝑇 =(𝑦1,⋯,𝑦𝑇)是长度为𝑇的标签序列。即在每个时刻 𝑡，都有一个监督信息 𝑦𝑡 ，我们定义时刻 𝑡 的损失函数为：

其中 𝑔(𝒉𝑡) 为第 𝑡 时刻的输出，L 为可微分的损失函数，比如交叉熵。那么整个序列的损失函数为：

整个序列的损失函数 L 关于参数 𝑼 的梯度为

即每个时刻损失 L𝑡 对参数 𝑼 的偏导数之和。

基于参数 𝑼 和隐藏层在每个时刻 𝑘(1 ≤ 𝑘 ≤ 𝑡) 的净输入有关，通过数学推导（推导过程比较复杂，这里略过，大家着重掌握公式），可以得出：

计算偏导数：

得到整个序列的损失函数 L 关于参数 𝑼 的梯度：

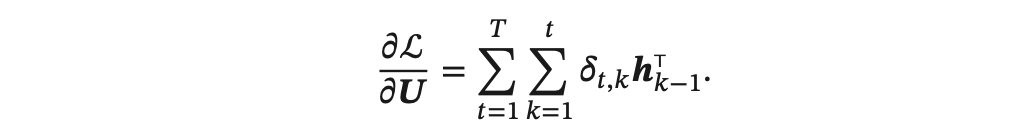
同理可得，L 关于权重 𝑾 和偏置 𝒃 的梯度为：

其中，类似前馈神经网络中的误差项为：

由上可以看出误差项，时刻k的𝛿𝑡,𝑘可以由时刻k+1的𝛿𝑡,𝑘+1得出，即所谓的反向传播。

下图给出了误差项随时间进行反向传播算法的示例：

二、进一步理解随时间反向传播算法BPTT

BPTT 的具体实现核心在于将 RNN 在时间维度上“展开”，从而把整个循环网络视作一个深层的前馈网络，然后利用反向传播算法计算每个时间步的梯度。以下是关键步骤：

（一）前向传播（Forward Pass）

在前向传播阶段，模型从初始隐藏状态开始，按时间顺序依次处理输入序列的每个时间步。在每个时间步 t 中，RNN 会计算出当前隐藏状态 ht：

同时，根据隐藏状态产生输出：

这些中间状态和输出都被存储下来，供之后的反向传播使用。

（二）损失计算

对于整个序列的输出，我们会计算一个总体损失 LL，它通常是所有时间步损失 LtL_t 的求和或平均：

例如，在一个回归或分类任务中，可能使用均方误差或交叉熵作为每个时间步的损失。

（三）时间展开（Unrolling）

为了使反向传播适用于循环结构，我们把 RNN 展开成一个由 T 个层组成的前馈网络，每一层对应一个时间步。虽然这些层共享同一组参数，但在展开的过程中，各个时间步之间的依赖关系（主要是隐藏状态 ht）得以显现。

这样做的目的是为了使我们能够用标准的反向传播算法计算梯度，从而更新整个序列中共享的参数。下面通过一个简单的例子说明这一过程。

假设情景

假设我们有一个 RNN 模型，用来处理一个长度为 3 的输入序列 [x1,x2,x3]（例如数值 1、2、3），初始隐藏状态 h0 设为零。模型的前向计算公式为：

将 RNN 展开成前馈网络

原始的 RNN 是通过循环实现的，即使用同一组参数不断将隐藏状态从前一步传递到下一步。为了直观地理解反向传播的过程，我们将其在时间轴上展开，即把每个时间步看作网络中的一层，这些层之间按照时间顺序相连。

对于我们的序列，有如下展开：

时间步 1
时间步 2
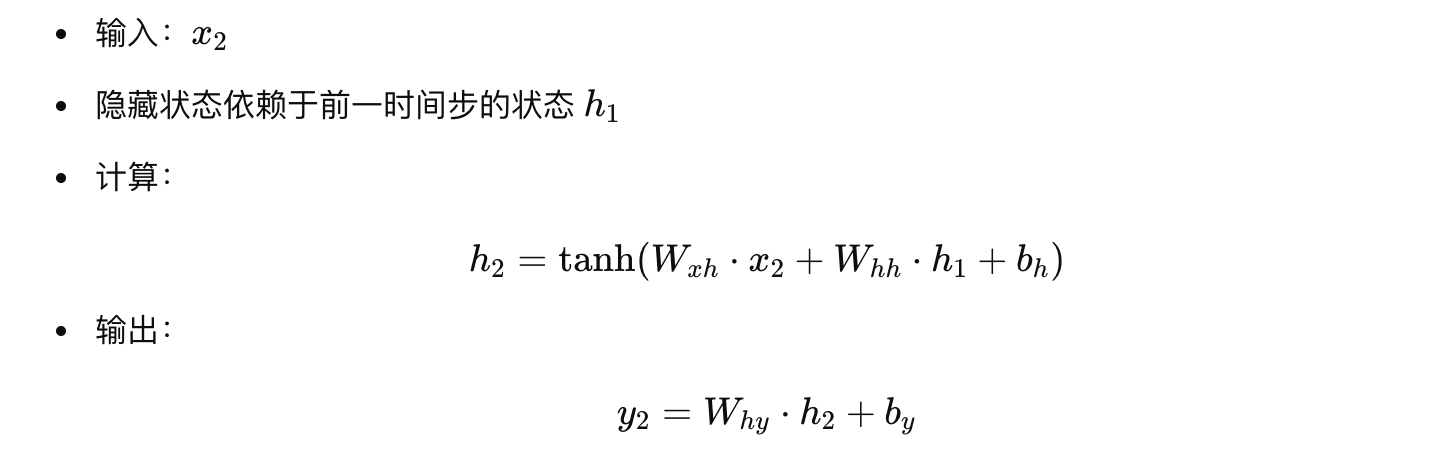
时间步 3

这整个过程就像一个前馈网络，共有 3 层（不包括初始状态），每层的输出 h_t 都依赖于前一层的输出 h_{t-1} 和当前输入 x_t 。注意，虽然在展开过程中每一层对应一个不同的时间步，但所有层共享同一组权重和偏置。

为什么这样展开？

这种展开方式将时序依赖“展开”到层级结构中，使得整个序列可以看成一个深层网络。这样有两个好处：

便于反向传播计算
我们可以像对普通前馈神经网络那样，基于链式法则逐层计算梯度，并且由于参数共享，每层计算的梯度会累积在同一组权重上。
捕捉长距离依赖
通过展开，我们能直观地理解误差如何从最后一层传回到第一层，反映长距离依赖问题，以及梯度消失或爆炸的问题。

总结

展开过程：将 RNN 从时间步 1 到 T 展开，每个时间步视为一层前馈网络，所有层使用同一组参数。
前向传播：依次计算每层隐藏状态和输出。
反向传播：从最后一层开始反向传播，逐层累积梯度，更新共享参数。

这种展开不仅使得梯度计算过程清晰，而且方便我们理解如何利用 BPTT 解决时间依赖问题，确保模型能够捕捉序列中长期和短期的信息。

（四）反向传播（Backward Pass Through Time，BPTT）

从展开后的最后一个时间步 T 开始，依次向前计算梯度：

局部梯度计算：在每个时间步，根据当前输出与目标之间的误差，首先计算当前时间步的输出层梯度，然后通过当前隐藏状态对损失的贡献，计算激活函数（如 tanh⁡）的导数。
梯度传递与累积：由于隐藏状态 hth_t 不仅直接影响当前输出，还间接影响后续所有时间步的输出，因而需要将来自未来时间步传回的梯度（往往称为 “dh_next”）与当前时间步的梯度相加，形成一个总的梯度。
参数梯度更新：利用链式法则，通过隐藏状态梯度计算出对输入到隐藏权重 Wxh 和隐藏到隐藏权重 Whh 以及偏置的梯度。由于这些参数在每个时间步都是共享的，每一步计算出的梯度都会被累加起来。
时间传递：在完成当前时间步梯度计算后，再将梯度通过传递回前一个时间步，继续重复这一过程直到第一个时间步。

下面以一个简单的 RNN 模型展开一个长度为 3 的序列的反向传播过程，来详细说明 BPTT 中的四个关键步骤：局部梯度计算、梯度传递与累积、参数梯度更新、和时间传递。假设模型的前向传播计算如下（激活函数采用 tanh）：

隐藏状态更新：
输出计算：

假设我们的损失函数 L 是所有时间步损失的加和：

其中每个时间步的损失 Lt 是模型输出 yt 和目标 (y_t)^{target} 之间的误差（例如均方误差）。

下面分步详细说明 BPTT 的反向传播过程。

1. 局部梯度计算

在反向传播时，我们需要先计算每个时间步在输出端的局部梯度，然后再传回隐藏层。具体来说：

对于时间步 t，我们先计算输出层的梯度：
接着，通过输出层将梯度传递给隐藏状态：
由于隐藏状态经过 tanh⁡ 激活，，其局部梯度部分需乘上激活函数的导数：

因此，得到当前时间步的局部梯度：

其中“⊙”表示元素级相乘。

这部分称为“局部梯度计算”，即对当前时刻输出误差先求到隐藏层（通过 Why），再结合激活函数求出对 zt 的梯度。

2. 梯度传递与累积

由于 RNN 中隐藏状态间存在依赖，当前时刻 ht 不仅受当前时间步损失 Lt 影响，还间接受到后续时间步的反馈。因此，反向传播时需要将未来时间步传回来的梯度累积在当前时刻。设我们计算总的梯度 dht 对隐藏状态的偏导，其计算方式为：

即当前时刻的总梯度等于当前局部梯度加上由下一时间步传回来的梯度经过隐藏层的权重传递后的结果。

3. 参数梯度更新

有了每个时间步的梯度 δt 和从后续传来的梯度累积，我们可以对各层参数求导。具体来说：

对于 输入到隐藏层权重 Wxh：

其中 ⊗ 表示外积，此处对每个时间步将 δt 与相应的输入 xt 外积，然后累加。
对于 隐藏到隐藏层权重 Whh：

同样每个时间步累加当前梯度与前一隐藏状态的外积。
对于 隐藏层偏置 bh：
对于 隐藏到输出层权重 Why，输出层的梯度已经在局部步骤中计算：
.
对于 输出偏置 by：

这些梯度在反向传播过程中在每个时间步内计算完毕后，通过累加得到整个序列上的梯度，接着就可以用常规优化方法更新参数。

4. 时间传递（从未来到过去）

在反向传播过程中，必须将未来时间步的梯度传递到当前时间步，这就是“时间传递”。具体步骤为：

这种梯度传递过程在整个序列反向迭代中重复执行，从时间步 T 逐层传回到时间步 1。

综合一个详细例子

假设我们有一个时间序列长度为 3 的 RNN，且以时间步 t=3 开始反向传播。简化起见，以下给出各步描述：

时间步 3：
时间步 2：
时间步 1：

总结

局部梯度计算：在每个时间步，根据输出误差乘以输出层权重和激活函数导数，得到对当前隐藏单元输入的梯度（δt）。
梯度传递与累积：从后向前逐步将未来时刻的梯度通过隐藏层（乘以和激活导数）传递给前一时间步，累加成当前时刻的总梯度。
参数梯度更新：利用每个时间步局部梯度与输入（或前一时刻隐藏状态）的外积，累积得到 Wxh、Whh 和 bh 的梯度；输出层参数的梯度也由对应输出误差累积。
时间传递：通过计算隐藏状态之间的依赖（即），将梯度从后续传递给当前，直至序列首端。