62.不同路径

力扣题目链接(opens new window)

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

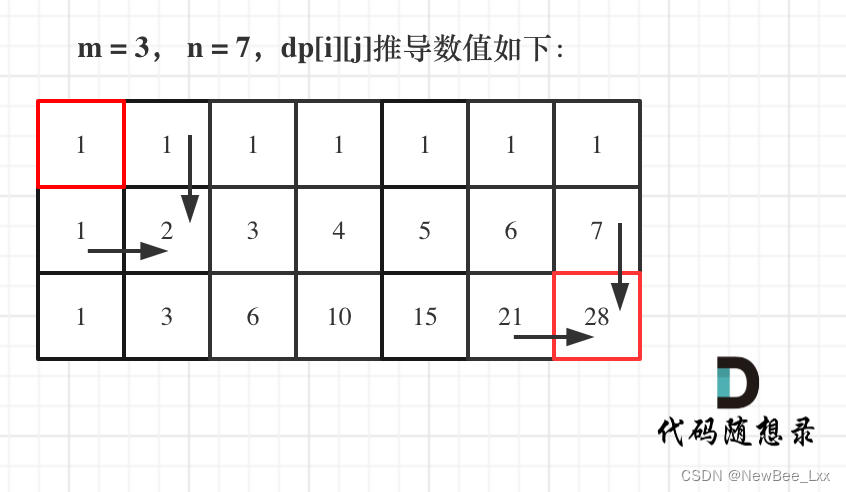
dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。

此时在回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j - 1]同理。

那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。

递推公式 因为到达某一点 只能从上面 或者是从左面来 那么到个点的方法就是 到上面那点的方法总数加上到左面那点的方法总数才是到这个点的方法总数

初始化最上排为1，最左排都为1，因为每次只能向上或者向左走一格，所以到达最上一排的每一个位置都只有一种方法，就是从起点一直往右走，左排同理

起始下标为0 所以终点下表是m-1,n-1

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m; i++) dp[i][0] = 1;
        for (int j = 0; j < n; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

63. 不同路径 II

力扣题目链接

m记录行 n记录列

如果起点和终点有障碍物说明不能到达终点了

定义一个全新的数组 dp 

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径

初始化：第一行和第一列都初始化为1 如果遇到障碍物停止初始化，因为障碍物之后是走不到的位置。

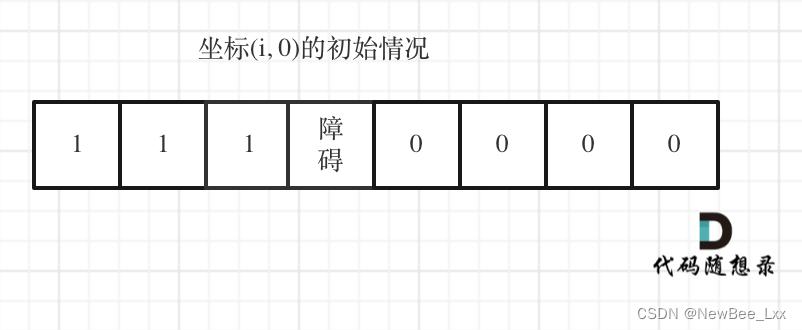
遍历：遇到障碍物直接continue跳过此次循环 因为到不了那里

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
	if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍，直接返回0
            return 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 1) continue;
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

343. 整数拆分

力扣题目链接(opens new window)

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。

可以想 dp[i]最大乘积是怎么得到的呢？

其实可以从1遍历j，然后有两种渠道得到dp[i].

一个是j * (i - j) 直接相乘。

一个是j * dp[i - j]，相当于是拆分(i - j)

也可以这么理解，j * (i - j) 是单纯的把整数拆分为两个数相乘，而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。

max里有dp[i]：因为i是固定的，j不断变换

for (int i = 3; i <= n ; i++) {
    for (int j = 1; j < i; j++) {
        dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
    }
}

优化

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n ; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
            }
        }
        return dp[n];
    }
};