0 基本介绍
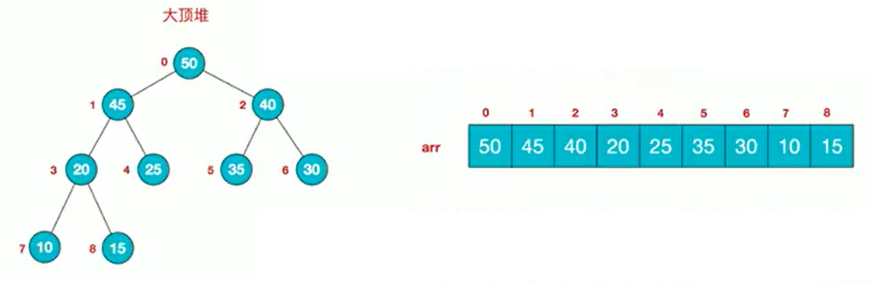
- 堆定义:首先是完全二叉树,分为大顶堆和小顶堆
- 大顶堆:顾名思义,如果将父子节点看成一个堆(三个节点的组合),那么顶的值需要大于其两个子节点的值,即顶大;小顶堆即顶小
- 升序排序使用大顶堆,降序使用小顶堆
- 回顾顺序存储二叉树中,父子节点的关系为:下标为n的节点,它的左子节点下标(2 * n + 1),右子节点(2 * n - 1),父节点(n-1) / 2;
- 回顾:顺序存储二叉树
- 回顾:排序算法-七大内排
1 思路图解
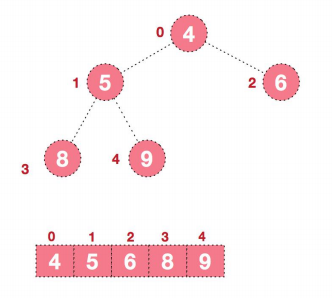
- 拿到n个元素的数组,就是得到了一个普通的顺序存储二叉树,也就是上面提到的普通的堆,堆大小为n
- 将堆调整成大顶堆,那么堆顶就是整个数组中的最大值了,将最大值和堆尾的值交换
- 抛开末尾的最大值,剩余的次小值构成一个大小为 n-1 的堆
- 对 n-1 大小的堆调整成新的大顶堆,堆顶(第二大元素产生)和该新大顶堆末尾交换,回到第3步
说明:
问:整体思路简单,就是不断构建大顶堆,首尾互换,难就难在如何调整,使得构建成满足条件的大顶堆呢?
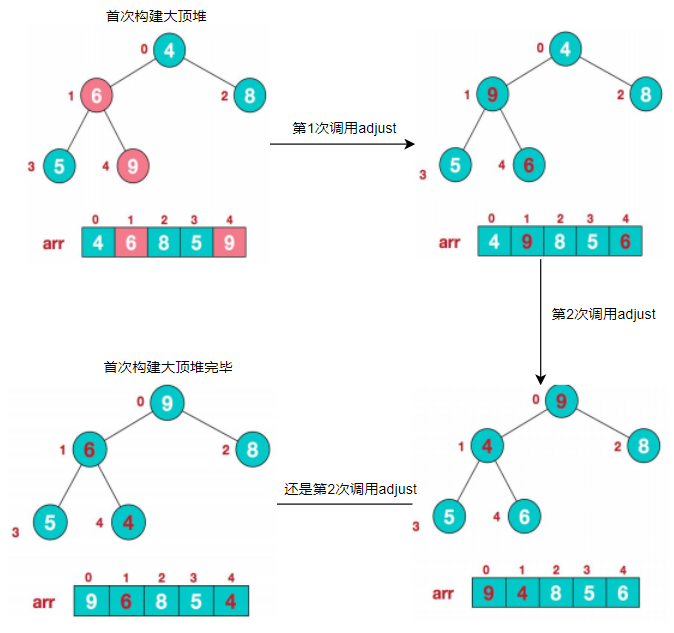
答:编写adjust方法,用以调整当前堆(a)为大顶堆,但是该方法并不是调用一次就能完成大顶堆,举例说明:如果将父子三节点看成是一个小小堆,那么从最后一个小小堆开始,使小小堆满足父值>子值(即大顶堆的要求),从后往前对小小堆的堆顶调用adjust方法,一直到第一个小小堆,从而实现构建大顶堆
注意:第一次调整时,堆(大小为n)是完全无序的,所以需要多次调用adjust,第一次调整完毕且首尾交换后,新堆(大小为n-1)的堆顶其左右子树其实就是两个大顶堆了,所以此时只需调用一次adjust,就能完成构建大顶堆.-----------------看下面图
00000000000000000000000分界线00000000000000000000000000
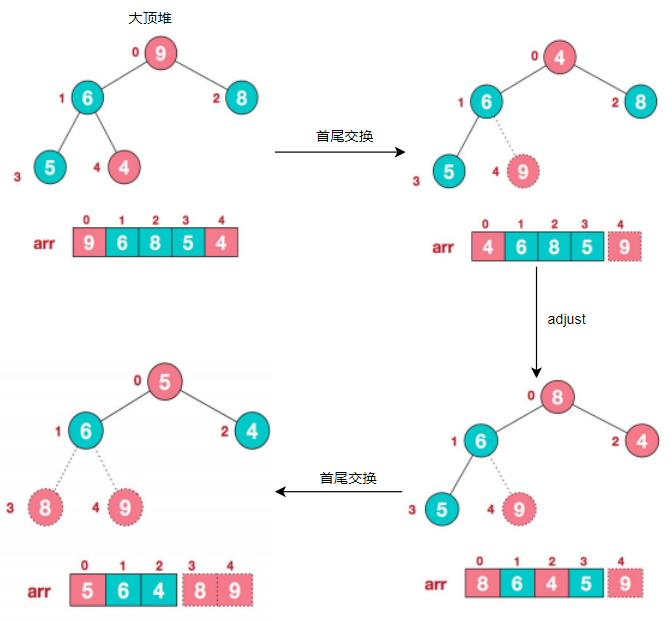
00000000000000继续调整,交换,最终得到升序数组000000000000000000
2 代码实现
//堆排序
public class App01_HeapSort {
public static void main(String[] args) {
int[] arr = {10, 20, 15, 25, 50, 30, 40};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
//堆排序方法
public static void heapSort(int[] arr) {
int temp = 0;
//从最后一个非叶子节点开始,从右往左,从下往上,调整堆,最终得到一个大顶堆
//最后一个非叶子节点下标:arr.length / 2 - 1
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjust(arr, i, arr.length);
}
//将大顶堆的堆顶(最大值)与末尾交换,并缩减调整区间
//调整剩余次小值的堆成为大顶堆,直到最终下标0和1交换,完成堆排序
//问:这里j范围表示堆就一个值,为什么还要执行操作? 因为这里是先交换再调整,因为0和1需要交换,所以j需要取1,只是j=1调整方法没有生效
for (int j = arr.length-1; j >=1; j--) {
temp = arr[0];
arr[0] = arr[j];
arr[j] = temp;
adjust(arr,0,j);
}
}
//调整 堆顶为节点i的堆 为大顶堆,前提是节点i的左右子树都是大顶堆
//问:该方法对传入的i有什么要求?
//答:目的不同,传入i不同
// 1.当初次构建大顶堆时,i应该从最后一个非叶子节点开始自减直到为0 (类似归并排序的先分后治)
// 2.非初次调整时,除了堆顶,下层所有都符合上大下小,就是说目的成了将堆顶元素从上往下找位置插入构建大顶堆,所以i就是堆顶0
public static void adjust(int[] arr, int i, int length) {
//取出堆顶值
int temp = arr[i];
//从上往下寻找插入位置同时,将较大值往上挪
for (int k = 2 * i + 1; k < length; k = 2 * k + 1) {
//使k指向左右子节点中较小的
if (k + 1 < length && arr[k] < arr[k + 1]) {
k++;
}
//类似插值排序的移位法,就是将较大值往上挪,直到找到合适的位置插入堆顶值,从而完成构建大顶堆
if (temp < arr[k]) {//这里为什么得用temp而不是arr[i]
arr[i] = arr[k];
i = k;
//为什么这里可以break?
//答:因为除了堆顶整体都符合上大下小,else表示堆顶比该层的节点大,即堆依然满足大顶堆,则堆无需调整
} else {
break;
}
}
arr[i] = temp;
}
}