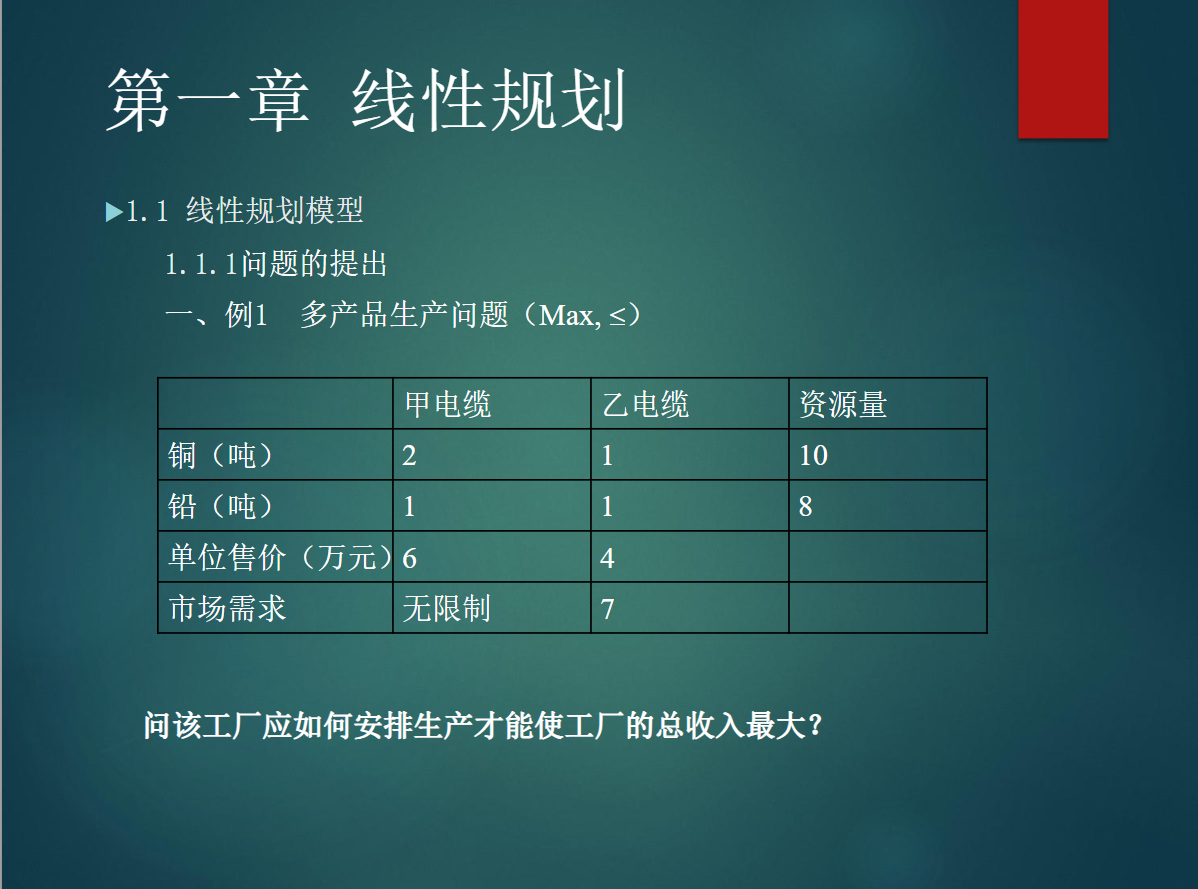
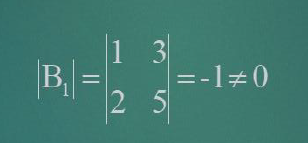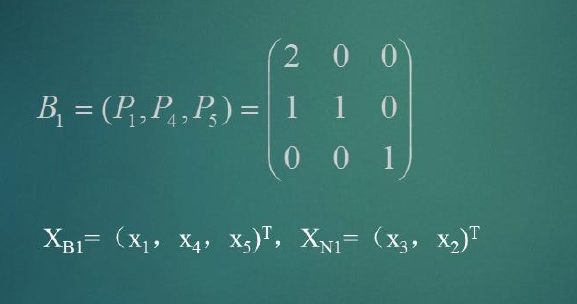第一章.线性规划

1.1例题

根据现实世界中的问题建立模型

一般表达式

①和式

②向量式

1.2变化标准：

1.3线性规划求解的基础原理和单纯解法

1.3.1解

①基础概念

• 基

• 可行解与基础解

• 其他分类

②判断举例

原式子：

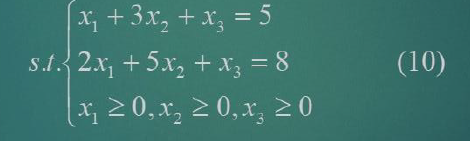
判断标准

将一个未知数作为常熟，其余两个组成矩阵，判断是否为0

结论：（判断解的类别）

1.3.2线性规划的基本定理

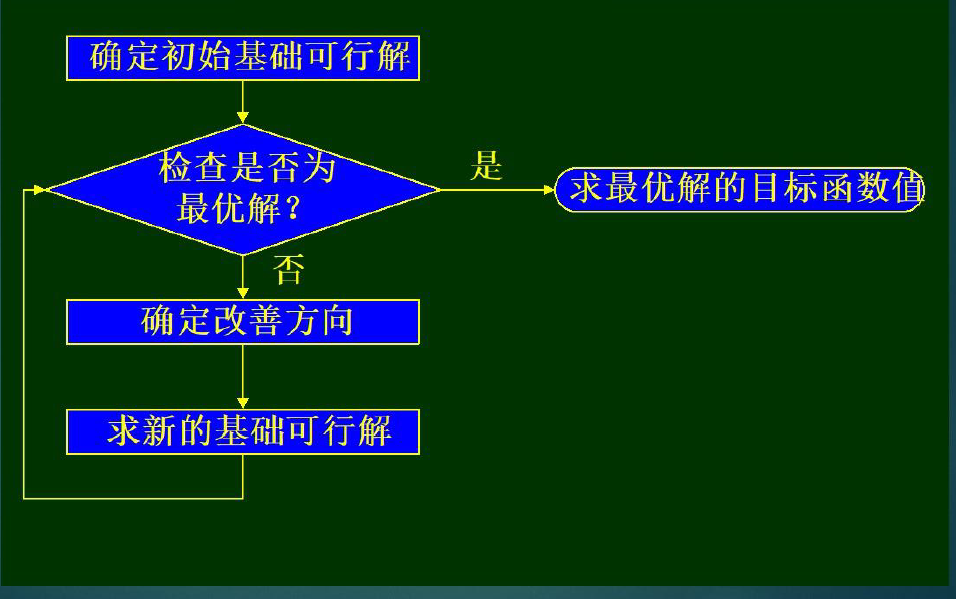
1.3.3单纯形法(求解最优可行解)

1.3.3.1基础步骤

1.3.3.2举例

x1作为基变量换入，x3作为非基变量换出

即：

重复上述操作即可

步骤总结：

符号化简原等式

结果的符号表示

表的形式（重点）

b：右端项

Cb：系数

Xb：基变量

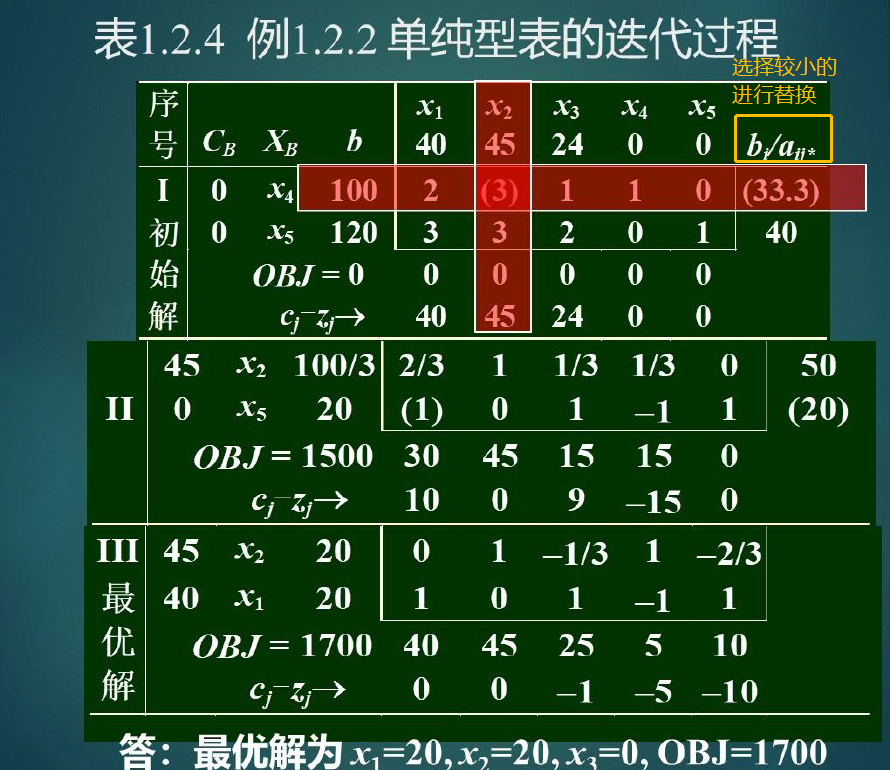
例子

将x4换出，将x2换入

1.3.4人工变量法

例：人工添加x6

假设x6前面系数为无限大（M）

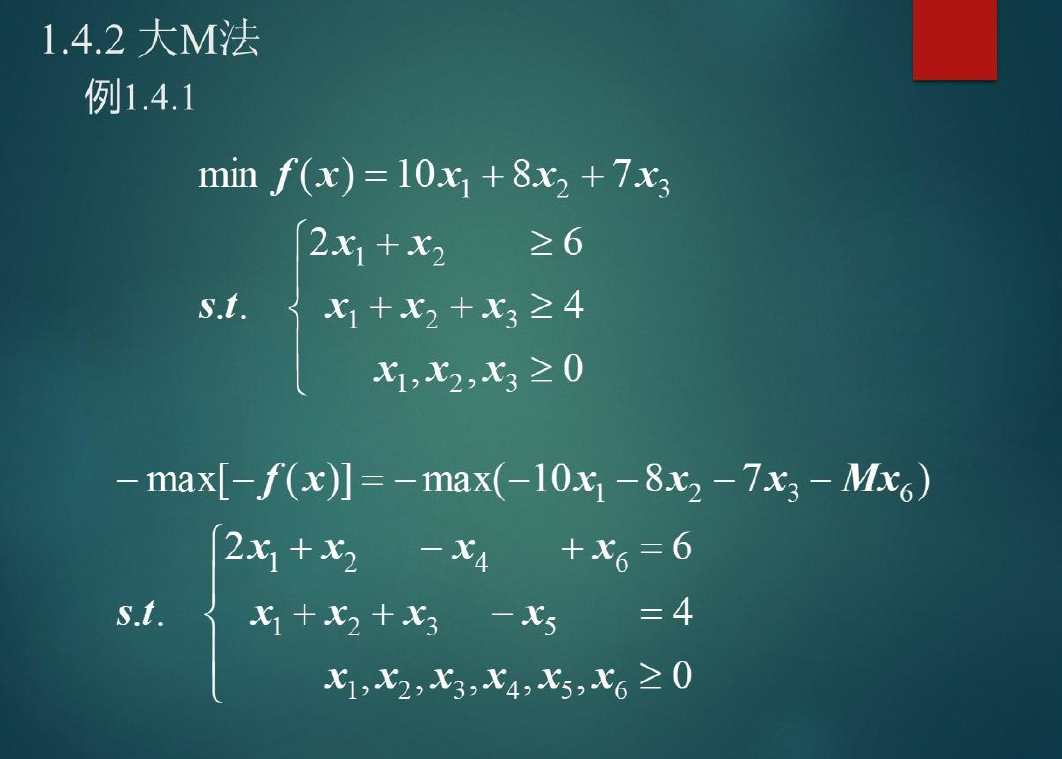
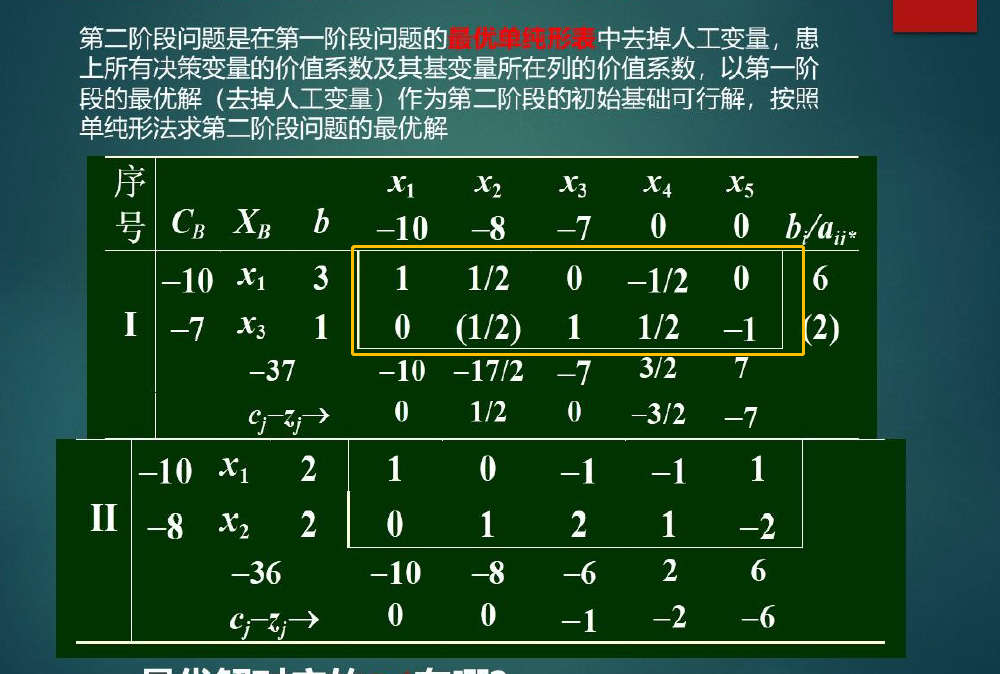
1.3.4.2两阶段法

举例：

第一个阶段:将人工变量去除

• 写第一阶段表 -->

• 第二阶段去掉人工变量x6，正常使用单纯形法计算即可

1.4基础建模步骤

第二章 对偶理论与灵敏度分析

2.1对偶问题

学习：

1. 对偶变换
2. 对偶定理理解
3. 对偶问题和原问题的解的关系

2.1.1背景模型（max，<=）的对偶变化

表总结（重要）

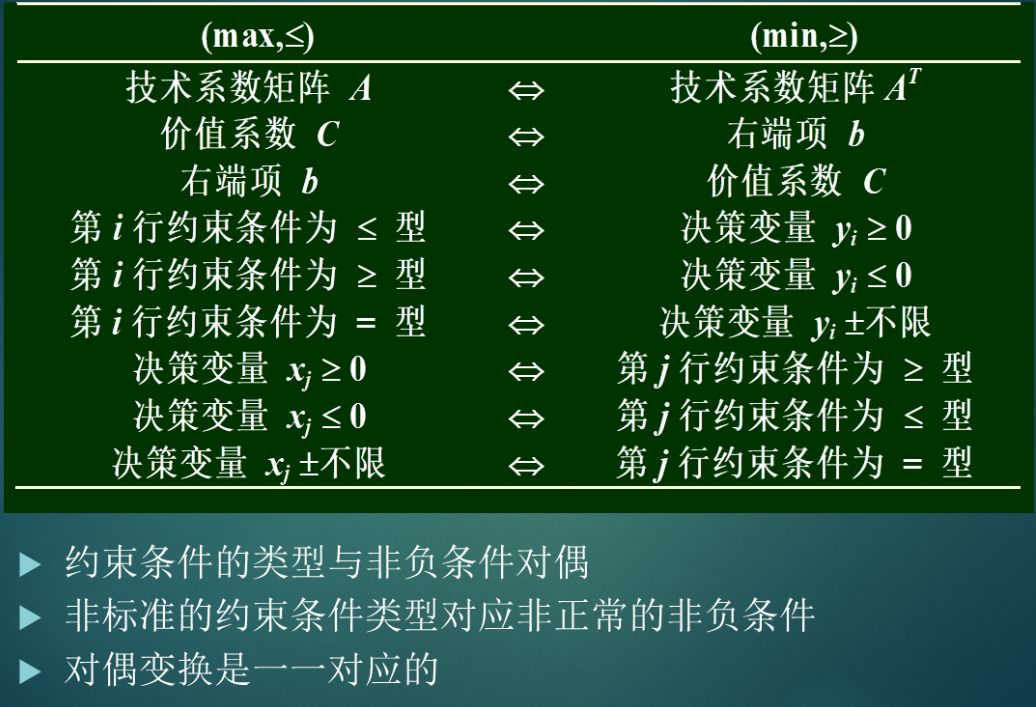
tips：

• 重点为一个约束行，对应一个决策变量

示例

2.1.2 线性规划的对偶定理

• 弱对偶定义

• 最优解判别定理

• 强对偶定理

• 互补松弛定理

U是原问题的松弛变量，V为对偶问题剩余变量

例：

松弛变量指代式子中补充的参数

互补松弛定理建立 对偶问题和原问题之间的关系

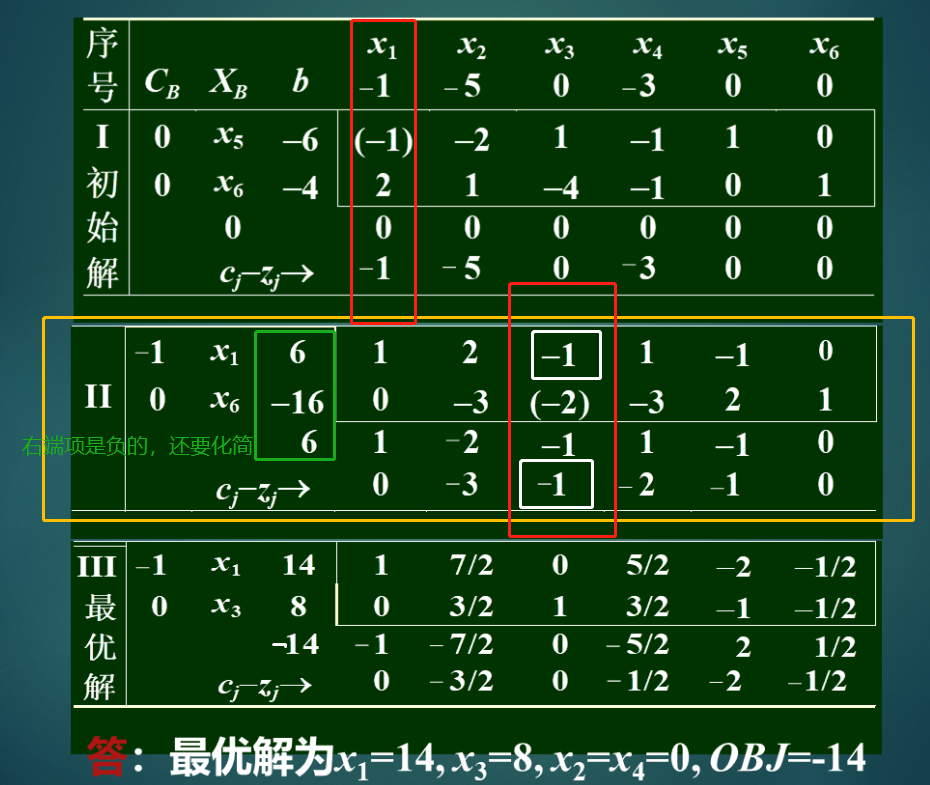
2.1.3 对偶单纯形法

• 步骤

最优检验改变，选较小值

• 例题

先将min转化为（<=）max函数（右端项为负）

标准值的右端项为负，所以使用对偶单纯形法

解：

2.2线性规划的灵敏度分析

2.2.1影子价格90（与最终松弛变量的Zi值相关）

影子价格等于松弛变量的Zi值（机会成本）

例
$$Z_j=技术系数\ast 影子价格$$

2.2.2价值系数的灵敏度分析

（Cj-Zj）检验数要保证恒为负数，使得最优条件不变

例：

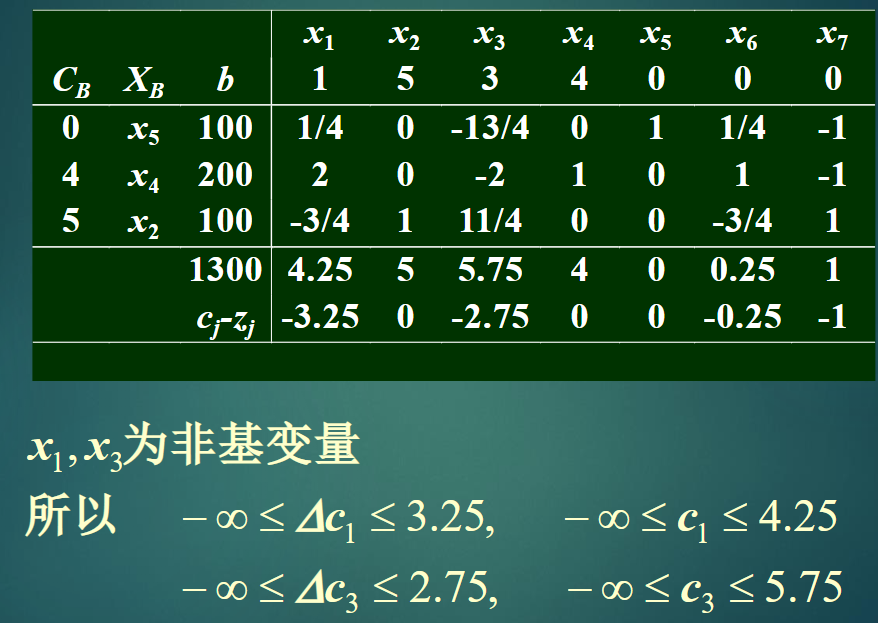
基变量的价值系数变化会影响到整体检验数（Cj-Zj）

2.2.3 右端项bi的灵敏度分析

B逆：松弛变量的系数矩阵

Xb：基础解（大于0）

2.2.4 技术系数aij的灵敏度分析

2.2.5新增决策变量的分析

将系数加入单纯性表中计算检验数即可

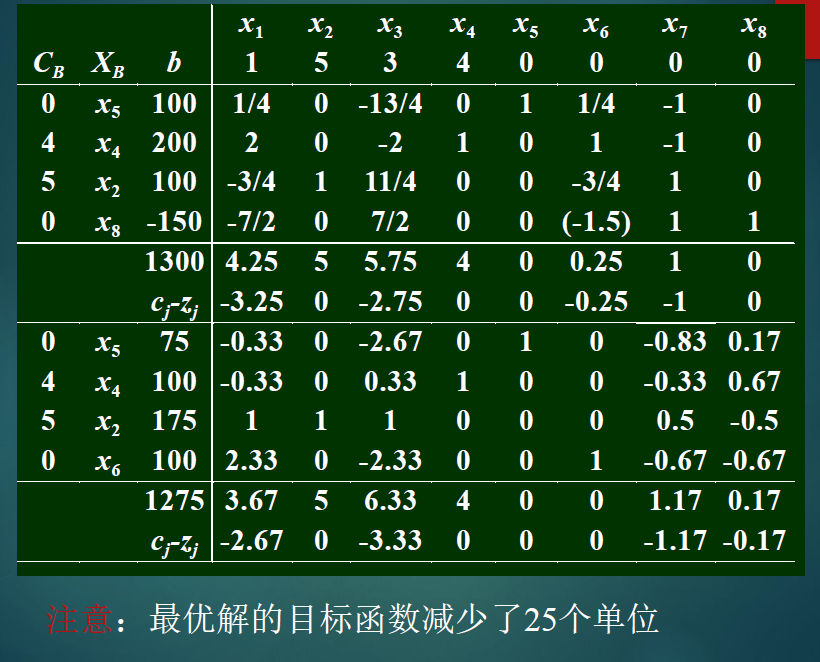
2.2.6新增约束条件的分析

• 先使用对偶单纯形法迭代

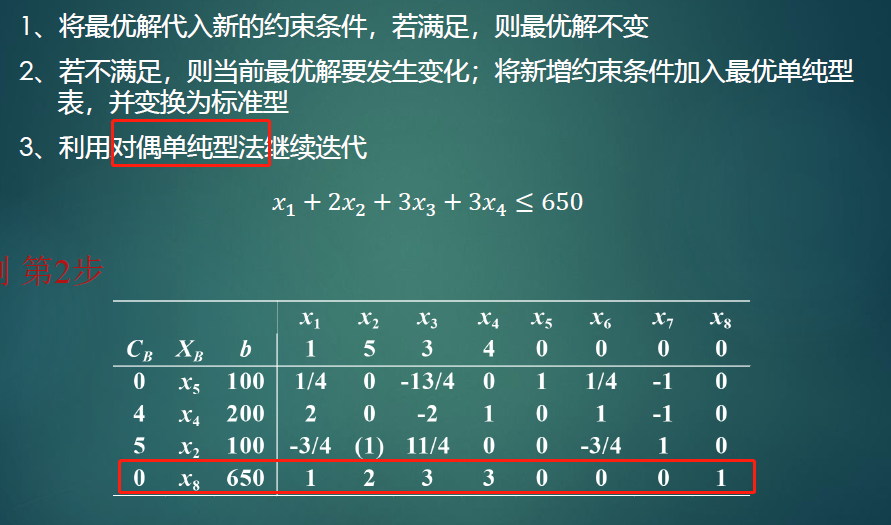
• ​ 转化成标准形式（x5/4/2/8）变为单位矩阵

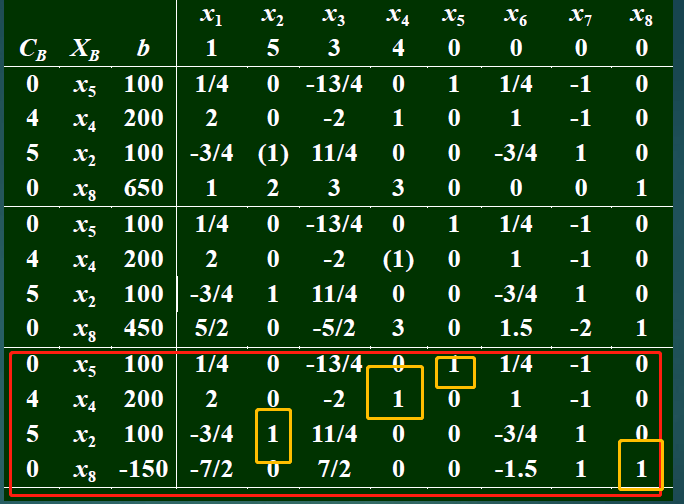
• 正常求解即可

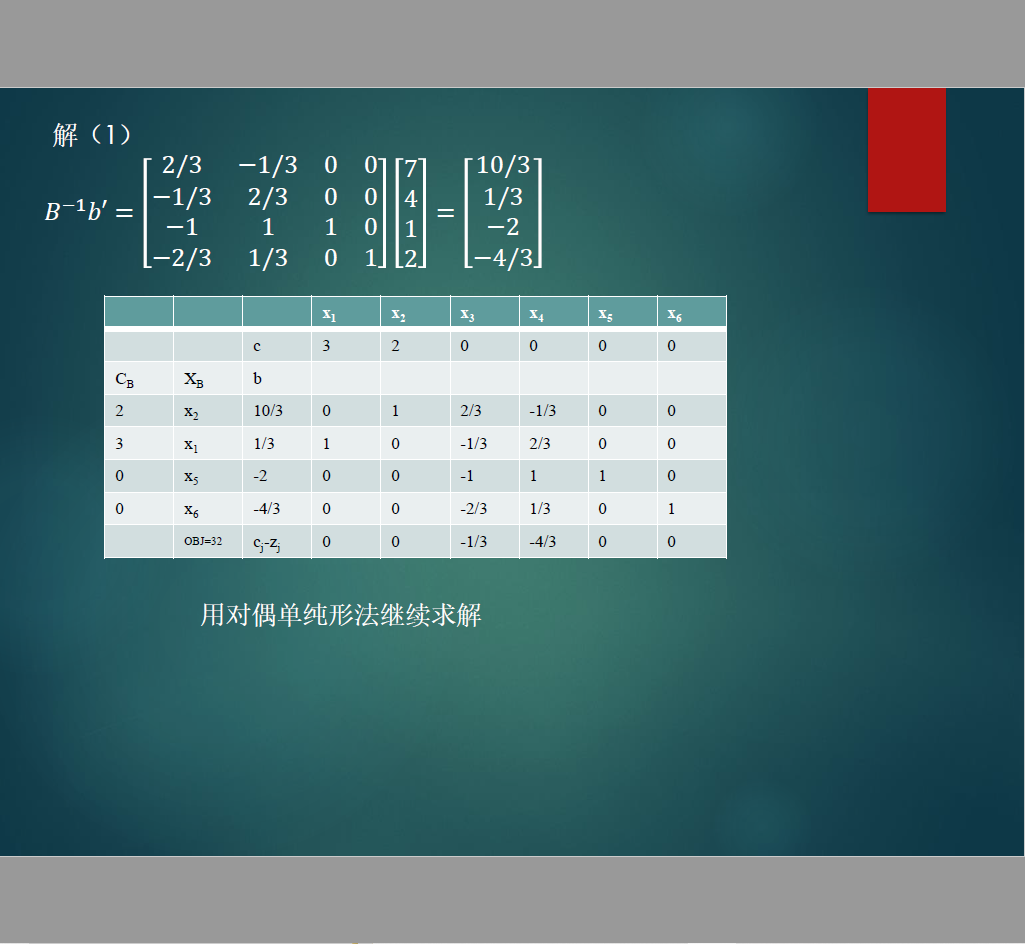
例题：

（1）

第三章 运输问题

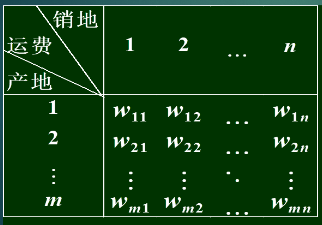
3.1 运输问题的一般数学模型

• m个地区生产，n个地区需要

决策变量可能很多，但是基变量很少

3.2运输问题求解

• 运费表

• 分配表

3.2.1 寻找初始可行解

首先：求基础可行解

其次：使用表上作业法使其变为最优解

• 西北角法

  

  根据行和列的剩余量，选择最小值

  例：

  

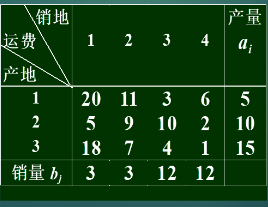
  解：

  

• 最低费用（推荐）

  每次都选择最小的利润，然后进行分配表的调整

  

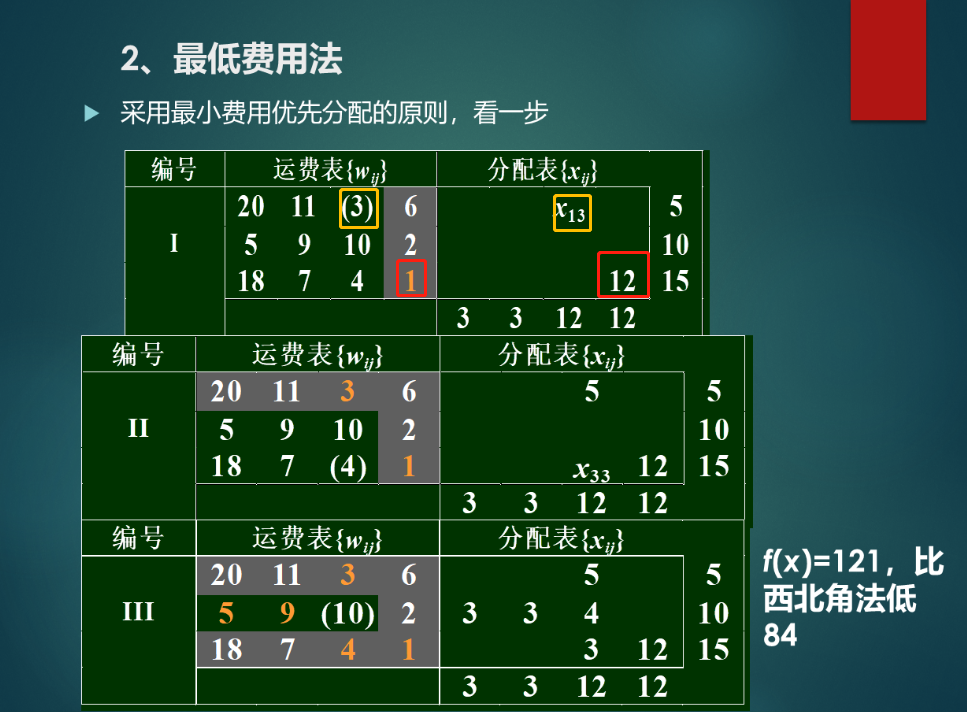
tips：（下节课问问行和列选择）

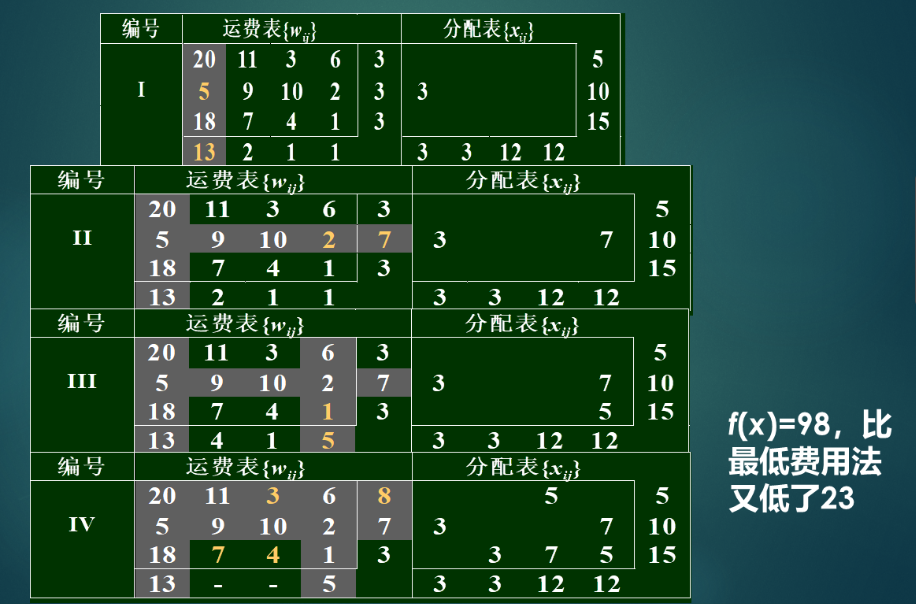
• 运费差额法（用每行或者每列中最小费用与次小之间的差额中选最大的）

  每次采用最大差额费用那行

  

3.2.2 利用位势法检验分配方案是否最优

运输问题可以类比为，Min问题（使费用最低）

即为
$$w\_ij-z\_ij\ge 0$$

第四条为重要公式

右表不为零的为基变量，为零的为非基变量

3.2.3 表上作业法/踏石法

$$Z_{ij}-w_{ij}<=0$$

例:

第四章 整数规划

分支定界问题

4.1 介绍

4.2 解法步骤

• 画出可行解区间，枚举
• 分支定界法

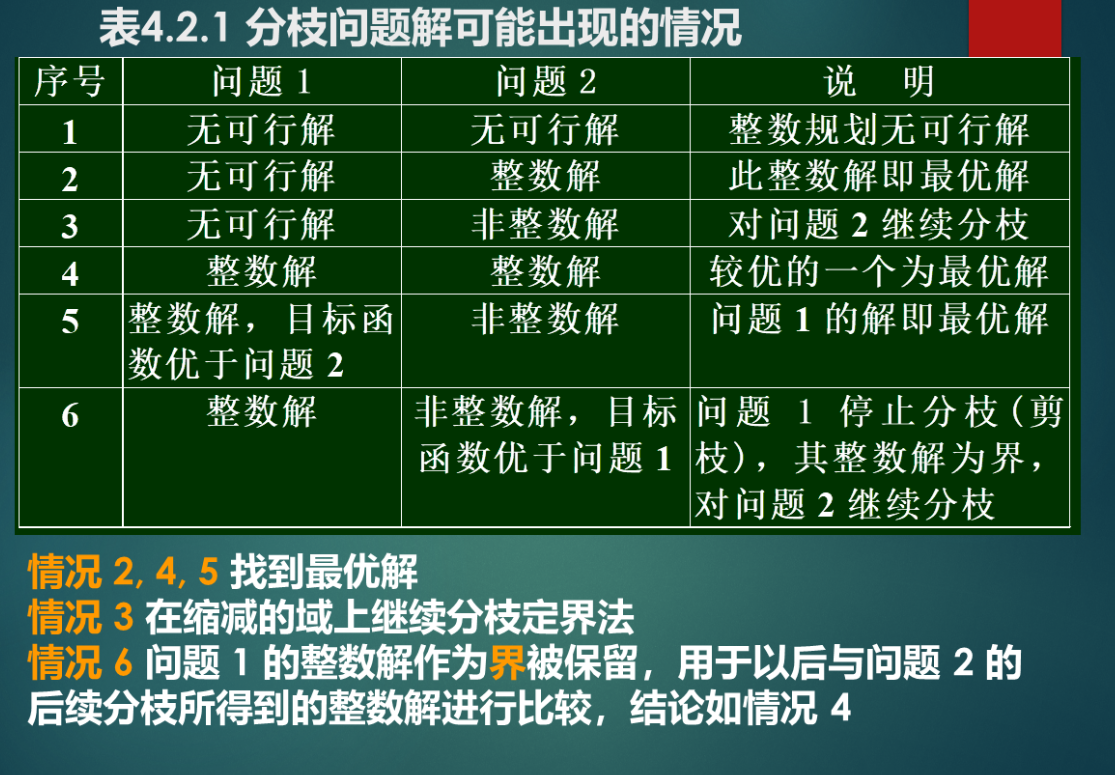
例：

出现的情况进行讨论

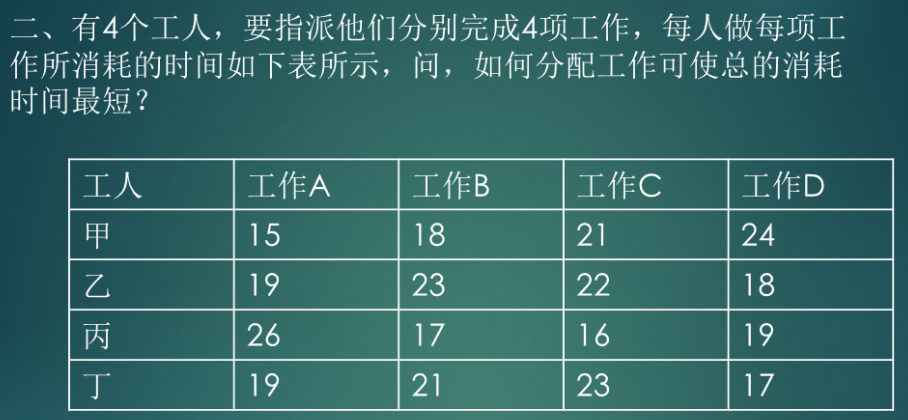
4.3 任务分配问题（匈牙利算法）

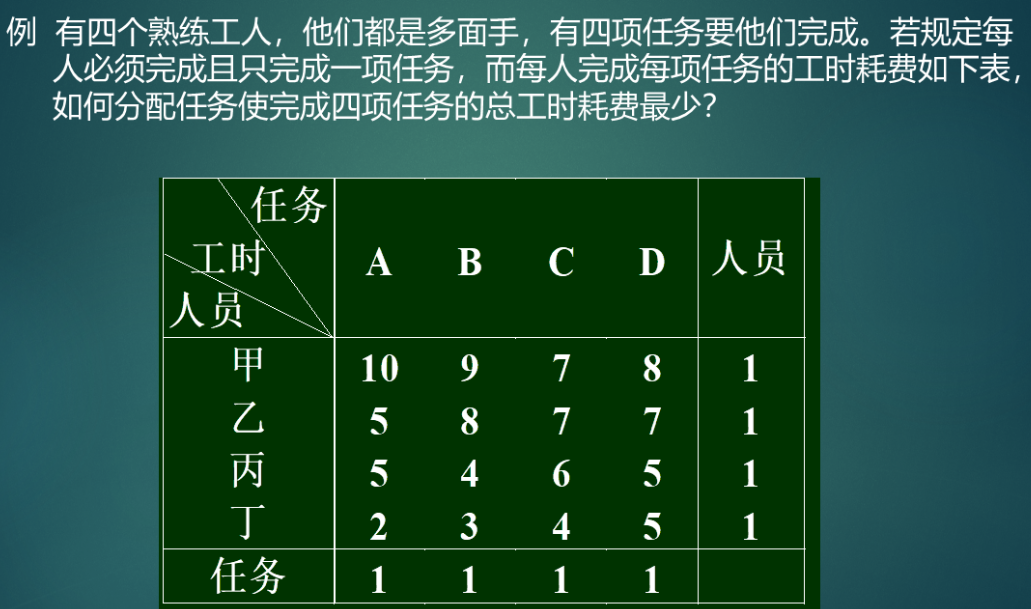
求解任务分配问题需要匈牙利算法

m为列数目

例：

第一步

第二步

tips

第三步

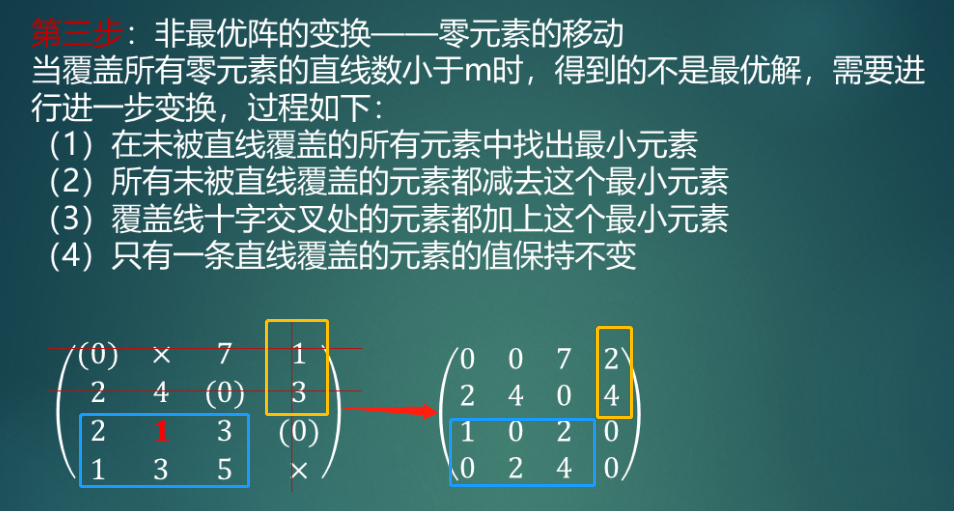
第四步

tips:两道例题

期中考试

• 线性规划

• 对偶理论

从max转为min

灵敏度分析

• 运输问题

• 整数规划

  • 分支定界

  

  • 任务分配